提高组模拟赛 37 C. 扰乱神器 题解
提高组模拟赛 37 C. 扰乱神器 题解
题意略
有一个很显然的性质,即对于一个块,其中的所有小块可能会变顺序,但不会变元素。
转化一下题意,对于单个块的单次翻转,对答案的变化即为原状态中的逆序对个数变为了顺序对个数,而顺序对个数其实就为总对数-逆序对个数-相等对个数。
我们通过归并排序的思想,以每一层左区间对右区间的逆序对数和相等对数,即可以 \(O(\log n)\) 计算单次翻转
如:\(3,4,2,1\),若使其长度为 \(4\) 的块翻转,即变为 \(1,2,4,3\),新的逆序对数即为 \(1,2\) 与 \(4,3\) 间产生贡献加上 \(1\),\(2\) 间的贡献和 \(3\),\(4\) 间的贡献。我们实际处理时便为 \(3,4\) 与 \(2,1\) 之间的总对数-顺序对+\(3,4\) 之间.....+\(1,2\) 之间.....
可以在 \(O(n\log n)\) 内求出单个块内每一层的逆序对数和相等对数,更合理的表达为每一层的跨块逆序、相等对数。
对于修改直接上线段树即可,复杂度为 \(O(n\log n+m\log^2n)\)。
其实上面的我认为官方题解比我讲的更好,但本题的实现很麻烦,我细致讲解一下:
主函数:
void solve() {
n = rd(), m = rd();
for(ll i = 1; i <= (1ll<<n); i++) a[i] = rd();
t.build(1, 1, 1ll<<n, n);
while(m--) {
ll q = rd(), l = rd(), r = rd(), siz = (1ll<<(n-q));
ll ans = 0;
t.modify(1, (l-1)*siz+1, r*siz, n-q, 1, 1ll<<n);
for(ll i = 0; i <= n-1; i++) ans += t.inp[1][i];
wr(ans);
}
}
简单的读入建树输出,记录答案时直接在总块上累加每一层的贡献
线段树:
struct SegTre {
ll ls[N<<1], rs[N<<1], lzy[N<<1], dep[N<<1];
ll inp[N<<1][25], equ[N<<1][25];
分别为左儿子,右儿子,懒标记,深度,逆序对个数,相等对个数,开 \(N<<1\) 即可是因为本题为满二叉树,刚刚好;深度这里是以长度为 \(1\) 的块为 \(0\),往上递增;后两个数组的第二维存储的是该块下每层的贡献(如第 \(0\) 层即为两个长度为 \(1\) 的块间的跨块贡献)。
void pushup(ll p) {
for(ll i = 0; i < dep[p]-1; i++) {
inp[p][i] = inp[ls[p]][i]+inp[rs[p]][i];
equ[p][i] = equ[ls[p]][i]+equ[rs[p]][i];
}
}
显然的正常向上传递
void update(ll p, ll v) {
lzy[p] ^= v;
for(ll i = 0; i < dep[p]; i++) {
if((v>>i)&1) inp[p][i] = (1ll << dep[p]+i-1) - equ[p][i] - inp[p][i];
}
if(v&(1ll<<(dep[p]-1))) swap(ls[p], rs[p]);
}
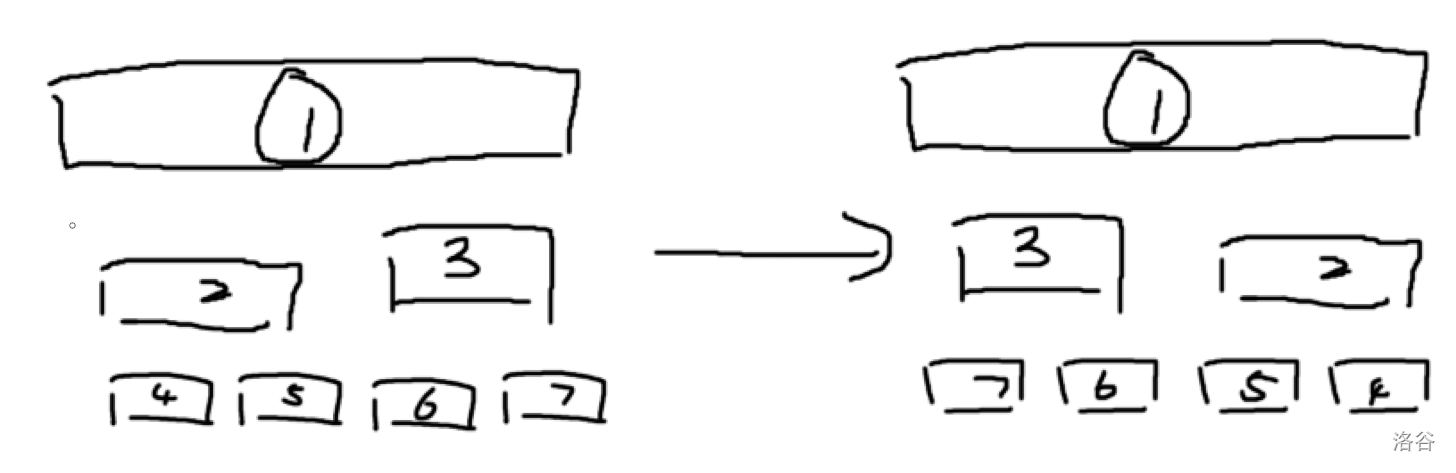
计算在一块中翻转的贡献,这里的 \(v\) 是类似状压的一个标记,第 \(i\) 位为 \(1\) 即第 \(i\) 位翻转,对于 \(1<<(dep[p]+i-1)\) 的理解,其实自己举个例子手模一下就可以了,如当深度为 \(3\) (长度为 \(8\)),\(i=1\) 时,实际上是两对跨两个长度为 \(2\) 的块之间的贡献,总对数即为 \(1<<3=8\)。而对于左右儿子的翻转,则直接交换即可,如下图:
void pushdown(ll p) {
if(lzy[p] == 0) return;
update(ls[p], lzy[p]);
update(rs[p], lzy[p]);
lzy[p] = 0;
}
略
void build(ll p, ll l, ll r, ll d) {
dep[p] = d;
if(l == r) return;
ls[p] = (p<<1), rs[p] = (p<<1|1);
ll mid = (l+r) >> 1;
build(ls[p], l, mid, d-1); build(rs[p], mid+1, r, d-1);
for(ll i = l; i <= mid; i++) cnt[a[i]]++;
for(ll i = mid+1; i <= r; i++) equ[p][d-1] += cnt[a[i]];
for(ll i = l; i <= mid; i++) cnt[a[i]]--;
ll i = l, j = mid+1, k = 0;
while(i <= mid && j <= r) {
if(a[i] <= a[j]) tmp[++k] = a[i], i++, inp[p][d-1] += j-mid-1;
else tmp[++k] = a[j], j++;
}
while(i <= mid) tmp[++k] = a[i++], inp[p][d-1] += j-mid-1;
while(j <= r) tmp[++k] = a[j++];
for(ll i = l; i <= r; i++) a[i] = tmp[i-l+1];
pushup(p);
}
在建树时,我们需要处理出来每一块每一层的跨块逆序对相等对数,逆序对直接采用了归并排序求法
void modify(ll p, ll l, ll r, ll x, ll L, ll R) {
if(l <= L && R <= r) {
update(p, (1ll<<x)-1);
return;
}
pushdown(p);
ll mid = (L+R) >> 1;
if(l <= mid) modify(ls[p], l, r, x, L, mid);
if(mid < r) modify(rs[p], l, r, x, mid+1, R);
pushup(p);
}
}t;
修改中的 \((1<<x)-1\) 即为如要翻转深度为 \(3\) 的块(长度为 \(8\)),\(v=7\) 即 \(0,1,2\) 层都要翻转,类似于上面的那个图。在修改时必须通过在函数中传递值域(即 \(L,R\)),因为这时的左右儿子只是编号,类似于动态开点。
总代码:
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
#define mst(x, y) memset(x, y, sizeof(x))
#define pii pair<ll, ll>
#define fi first
#define se second
#define mp(x, y) make_pair(x, y)
#define eb emplace_back
inline ll rd(){ll x = 0, f = 1;char c = getchar();while(c < '0' || c > '9'){if(c == '-') f = -1;c = getchar();}while(c >= '0' && c <= '9'){x = (x<<1)+(x<<3)+(c^48);c = getchar();}return f*x;}
inline void writ(ll x){if(x < 0){putchar('-');x = -x;}if(x > 9) writ(x/10);putchar(x%10 | 0x30);return;}
inline void wr(ll x){writ(x);puts("");}
inline void wr_(ll x){writ(x);putchar(' ');}
const ll N = (1ll<<20)+5, inf = 0x3f3f3f3f;
bool st;
ll n, m;
ll a[N], cnt[N], tr[N], tmp[N];
struct SegTre {
ll ls[N<<1], rs[N<<1], lzy[N<<1], dep[N<<1];
ll inp[N<<1][25], equ[N<<1][25];
void update(ll p, ll v) {
lzy[p] ^= v;
for(ll i = 0; i < dep[p]; i++) {
if((v>>i)&1) inp[p][i] = (1ll << dep[p]+i-1) - equ[p][i] -inp[p][i];
}
if(v&(1ll<<(dep[p]-1))) swap(ls[p], rs[p]);
}
void pushup(ll p) {
for(ll i = 0; i < dep[p]-1; i++) {
inp[p][i] = inp[ls[p]][i]+inp[rs[p]][i];
equ[p][i] = equ[ls[p]][i]+equ[rs[p]][i];
}
}
void pushdown(ll p) {
if(lzy[p] == 0) return;
update(ls[p], lzy[p]);
update(rs[p], lzy[p]);
lzy[p] = 0;
}
void build(ll p, ll l, ll r, ll d) {
dep[p] = d;
if(l == r) return;
ls[p] = (p<<1), rs[p] = (p<<1|1);
ll mid = (l+r) >> 1;
build(ls[p], l, mid, d-1); build(rs[p], mid+1, r, d-1);
for(ll i = l; i <= mid; i++) cnt[a[i]]++;
for(ll i = mid+1; i <= r; i++) equ[p][d-1] += cnt[a[i]];
for(ll i = l; i <= mid; i++) cnt[a[i]]--;
ll i = l, j = mid+1, k = 0;
while(i <= mid && j <= r) {
if(a[i] <= a[j]) tmp[++k] = a[i], i++, inp[p][d-1] += j-mid-1;
else tmp[++k] = a[j], j++;
}
while(i <= mid) tmp[++k] = a[i++], inp[p][d-1] += j-mid-1;
while(j <= r) tmp[++k] = a[j++];
for(ll i = l; i <= r; i++) a[i] = tmp[i-l+1];
pushup(p);
}
void modify(ll p, ll l, ll r, ll x, ll L, ll R) {
if(l <= L && R <= r) {
update(p, (1ll<<x)-1);
return;
}
pushdown(p);
ll mid = (L+R) >> 1;
if(l <= mid) modify(ls[p], l, r, x, L, mid);
if(mid < r) modify(rs[p], l, r, x, mid+1, R);
pushup(p);
}
}t;
bool ed;
void solve() {
n = rd(), m = rd();
for(ll i = 1; i <= (1ll<<n); i++) a[i] = rd();
t.build(1, 1, 1ll<<n, n);
while(m--) {
ll q = rd(), l = rd(), r = rd(), siz = (1ll<<(n-q));
ll ans = 0;
t.modify(1, (l-1)*siz+1, r*siz, n-q, 1, 1ll<<n);
for(ll i = 0; i <= n-1; i++) ans += t.inp[1][i];
wr(ans);
}
}
signed main() {
freopen("dr.in", "r", stdin);
freopen("dr.out", "w", stdout);
ll T = 1;
while(T--) solve();
cerr << "Time :" << 1.0*clock() / CLOCKS_PER_SEC << "s\n";
cerr << "Memory :" <<( (&ed-&st) / (1ll<<20) ) << "MB\n";
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号