[线段树系列 #5] 可持久化线段树

[线段树系列 #5] 可持久化线段树

简单介绍

可持久化线段树，为什么是可持久化的呢，因为他能调取线段树上的历史数据。

思路概述

可持久化线段树的简单思路就是，在动态开点线段树的基础上，每次修改时建一棵新树，并将没有修改的节点直接指向原有的节点，使得可以在较短的时间内完成操作。这里插一张网上的图，辅助理解。

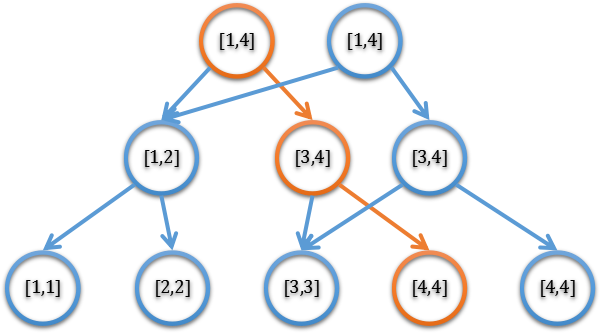
可持久化数据结构，一般用来求区间的一个信息（如经典例题求区间第k小数）或是调取历史信息。

而在求区间信息时，大多为在询问时一边向更深节点走一边限制边界。

而可持久化结构所给予的支持即为 1.调取[1~r]段的信息 2.调取[1~l-1]段的边界

具体实现

通常操作为：离散化后先按照值域建一棵空树，然后将每个节点依次插入，最后开始处理操作

插入节点时，按上述思路来说即为新建一条链，所以具体实现上为先继承上个版本当前点的左右儿子，然后按照值的大小选择新建节点为左儿子或右儿子。

在下面的例题P3834 【模板】可持久化线段树 2，即求静态 \([l,r]\) 的第 \(k\) 小值中，我们通过可持久化线段树的区间可加减性，由 \([1,r]-[1,l-1]\) 求得 \([l,r]\) 的答案

// 例题：求[l,r]第k小值
void build(int &p, int l, int r){
	p = ++cnt;
	if(l == r) return;
	int mid = (l+r) >> 1;
	build(t[p].l, l, mid);
	build(t[p].r, mid+1, r);
}
void update(int &p, int lst, int l, int r, int x){
	p = ++cnt;
	t[p] = t[lst]; t[p].val++;
	if(l == r) return;
	int mid = (l+r) >> 1;
	if(x <= mid) update(t[p].l, t[lst].l, l, mid, x);
	else update(t[p].r, t[lst].r, mid+1, r, x);
}
int query(int L, int R, int l, int r, int k){
	if(l == r) return l;
	int mid = (l+r) >> 1, x = t[t[R].l].val-t[t[L].l].val;
	if(x >= k) return query(t[L].l, t[R].l, l, mid, k);
	else return query(t[L].r, t[R].r, mid+1, r, k-x);
}

而在下一道例题，P2633 Count on a tree，即求树上两点间点权的第 \(k\) 小值中，我们也同样可以利用上述性质，结合树上差分，答案即为\([1,u]+[1,v]-[1-lca]-[1,fa[lca]]\)。具体实现即为修改在 \(query\) 操作中的 \(x\) 变量进行限制。

void update(int &p, int q, int l, int r, int v){
	p = ++cnt;
	t[p] = t[q]; t[p].val++;
	if(l == r) return;
	int mid = (l+r) >> 1;
	if(v <= mid) update(t[p].l, t[q].l, l, mid, v);
	else update(t[p].r, t[q].r, mid+1, r, v);
}
int query(int a, int b, int c, int d, int l, int r, int k){
	if(l == r) return l;
	int mid = (l+r) >> 1, x = t[t[a].l].val+t[t[b].l].val-t[t[c].l].val-t[t[d].l].val;
	if(k <= x) return query(t[a].l, t[b].l, t[c].l, t[d].l, l, mid, k);
	else return query(t[a].r, t[b].r, t[c].r, t[d].r, mid+1, r, k-x);
}
void bfs(){
	queue <int> q;
	q.push(1);
	d[1] = 1;
	while(q.size()){
		int t = q.front(); q.pop();
		for(int i = hd[t]; i; i = nxt[i]){
			int y = ver[i];
			if(d[y]) continue;
			update(rt[y], rt[t], 1, len, v[y]);
			d[y] = d[t]+1, f[y][0] = t;
			for(int j = 1; j <= 20; j++)
				f[y][j] = f[f[y][j-1]][j-1];
			q.push(y);
		}
	}
}
void solve(){
    lsh();
	build(rt[0], 1, len);
	update(rt[1], rt[0], 1, len, v[1]);
	bfs();
}

而维护可持久化线段树过程中，则从原来的 \(update(rt[i],rt[i-1],...)\) 变为 \(update(rt[u],rt[fa[u]],...)\)。这也是可持久化线段树多种运用的一个举例，即通过一些前后信息来建树。