DS
算法可视化网站
- https://gallery.selfboot.cn/zh/algorithms
- https://www.cs.usfca.edu/~galles/visualization/Algorithms.html
栈, 队列, 数组
队列
循环队列
初始: Q.front = Q.rear = 0
队首指针进1: Q.front = (Q.front + 1) % MaxSize
队尾指针进1: Q.rear = (Q.rear + 1) % MaxSize
出入队: 指针都顺时针进1
判空的3种方法
1. 牺牲一个单元来区分
队满: (Q.rear + 1) % MaxSize = Q.front
队空: Q.front = Q.rear
队长: (Q.rear - Q.front + MaxSize) % MaxSize
2. 类型中设置size,数据成员
3. 类型中设置tag数据成员, 区分是删除还是增加元素
数组
特殊矩阵
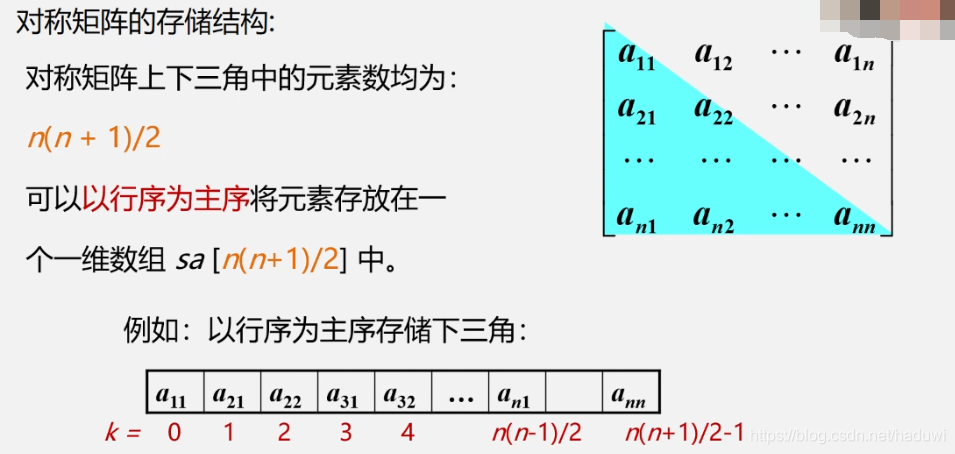
串
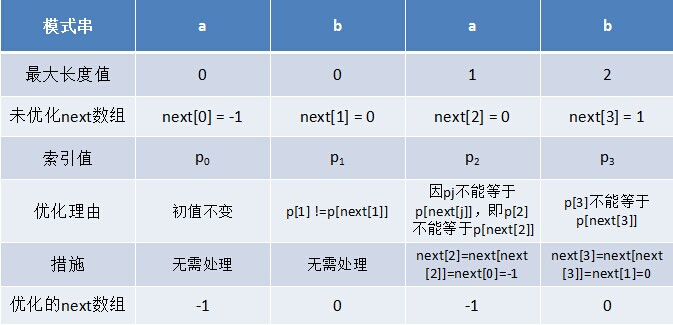
Kmp
失配时,模式串向右移动的位数为:已匹配字符数 - 失配字符的上一位字符所对应的最大长度值
next 数组相当于“最大长度值” 整体向右移动一位,然后下标[0]赋为-1
失配时,模式串向右移动的位数为:失配字符所在位置 - 失配字符对应的next 值

只要出现了p[next[j]] = p[j]的情况,则把next[j]的值再次递归
如果模式串的后缀跟前缀相同,那么它们的next值也是相同的
树
满二叉树, 完全二叉树
线索二叉树
应用
哈夫曼树
- 构造
森林中节点权最小的两个组成一个新的结点, 结点权值 = 两个子权值相加, 构成一棵树,
将这两个结点消去, 新的结点放入原来的森林中
反复找森林中最小的两个, 直至森林只有一棵树
并查集
优化

图
应用
存储结构
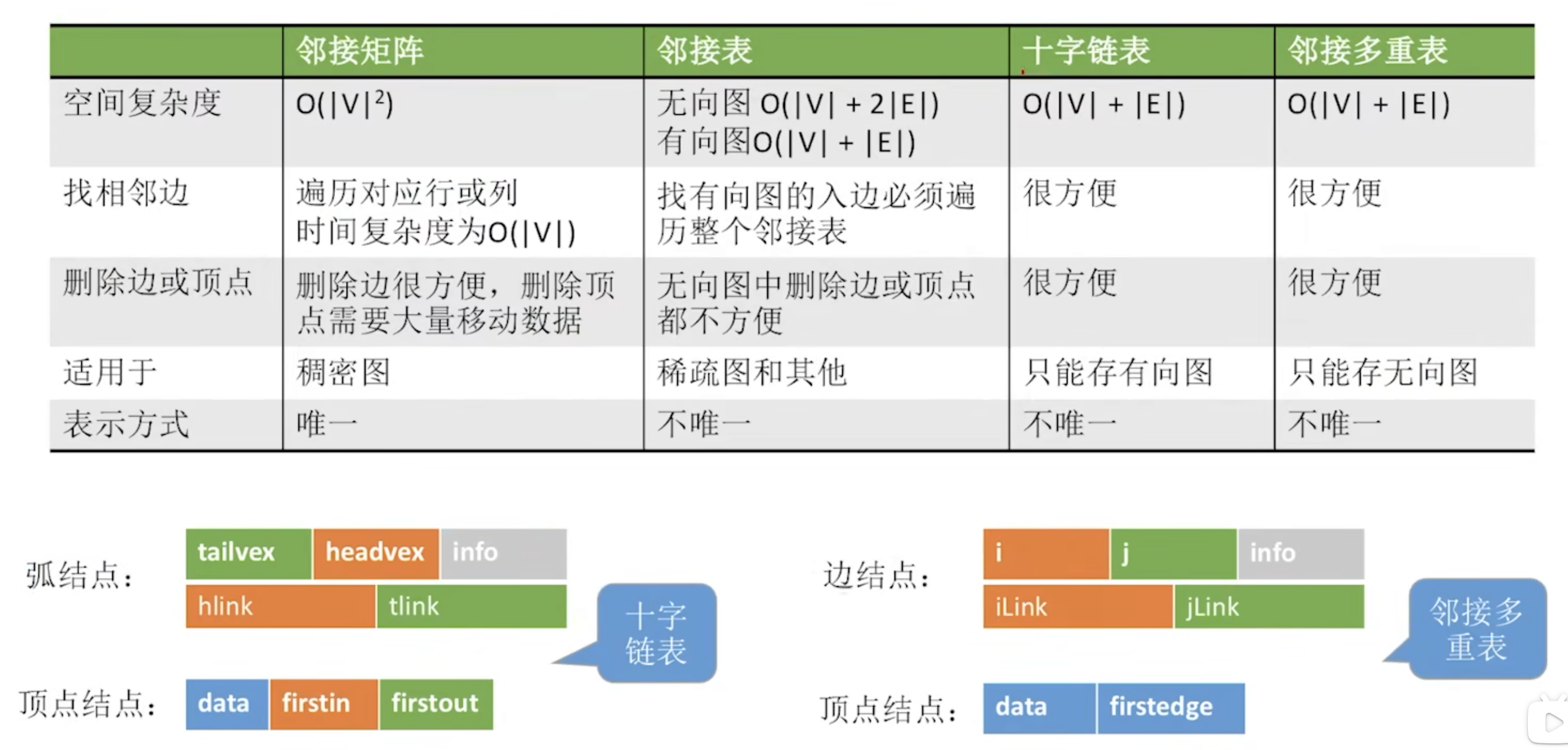
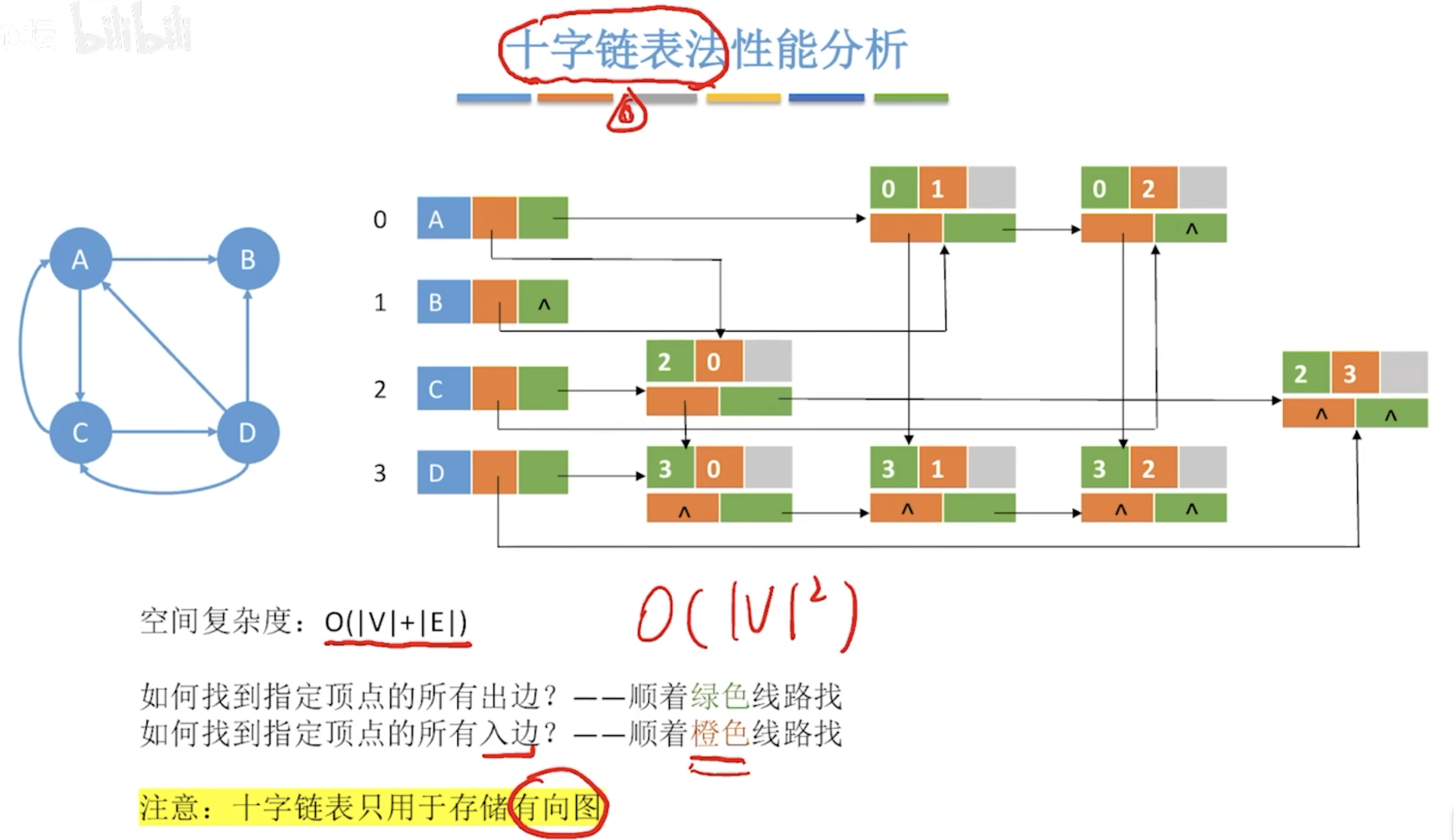

遍历
应用
1. 最小生成树
2. 最短路径
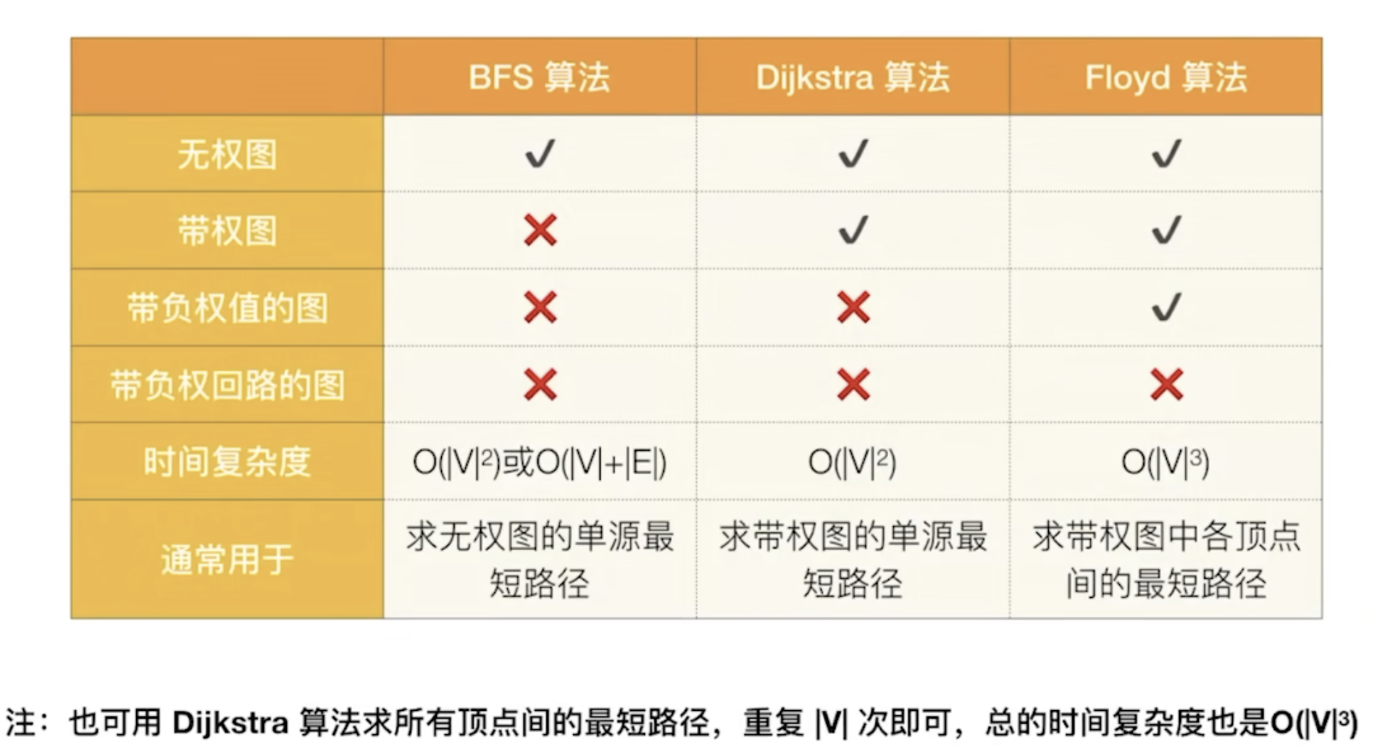
3. 拓扑排序
查找
掌握: 折半查找, 构造判定树, 分析平均查找长度
了解: 二叉排序树, 二叉平衡树, 红黑树 -> 概念, 性质, 相关操作
掌握: B树 增删查
了解: B+树基本概念和性质
掌握散列表的构造, 冲突处理方法, ASL, 特征, 性能分析
树
二叉排序树 (BST)
重点
定义
删除操作
平均查找长度的计算
左子树上所有结点的关键字均小于根节点的关键字
左子树节点值 < 根节点值 < 右子树节点值
-
插入
若原二叉树为空, 则直接插入结点, 否则, 若关键字k <根节点, 则插入左子树; > 根节点插入右子树 -
删除
1) 被删除结点z是叶结点, 则直接删除
2) z有且只有一棵子树, 直接把子树提上来
3) 若结点z有左右两个子树, 就用z的直接前驱(左子树的最右下节点) 或直接后继(右子树的最左下结点) 替代z, 从二叉排序树中删去这个直接前驱或直接后继, 转换为前两种情况. -
查找效率分析
主要与树高有关,
最好情况: 最小高度为$log_2n + 1$ , 平均查找长度(ASL) $O(log_2n)$
最差情况: 节点都在同一棵子树上, 查到最底层, $O(n)$
执行增删平均时间$log_2n$
适用于动态查找表要提高查找效率, 需要减少树的高度, 引入了平衡二叉树
平衡二叉树(AVL)
插入新结点后如何调整"不平衡"问题
平衡因子: 此节点往下 左子树深度 - 右子树深度
保持
$$
左孩子值 < 根值 < 右孩子值
$$
旋转之后把自己的孩子丢给别人,左旋丢左孩子,右旋丢右孩子
- 插入与调整平衡
插入操作导致"最小不平衡子树"高度 + 1, 只要将他调整为平衡, 则其他祖先节点都会恢复平衡
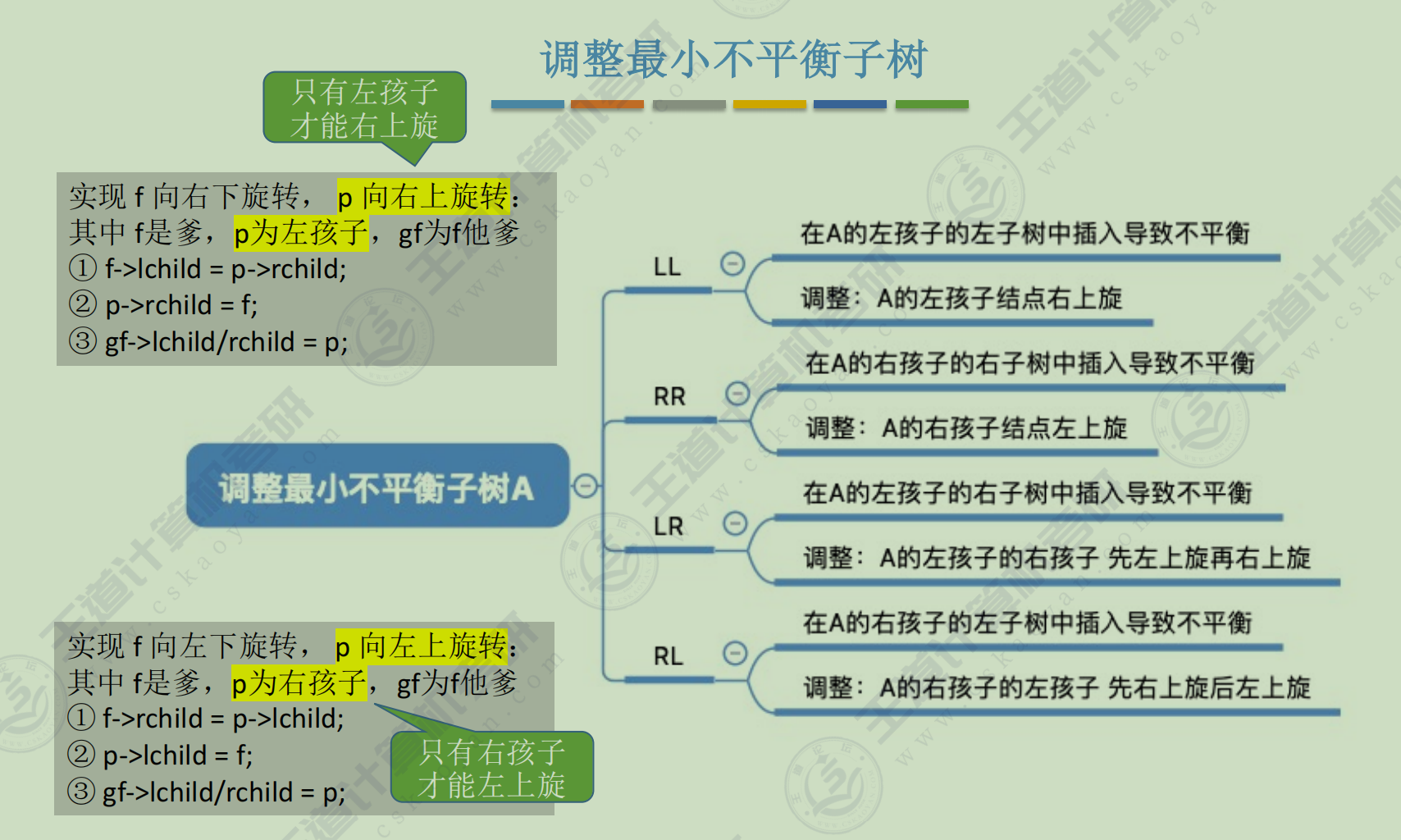
节点数目一定时,平衡因子为±1时,树最高。
| 层 | 节点总数 |
|---|---|
| 1 | 1 |
| 2 | 2 |
| 3 | 4 |
| 4 | 7 |
| 5 | 12 |
| 6 | 20 |
| 7 | 33 |
- 删除
① 删除节点 (同二叉排序树)
② 北伐找到最小不平衡子树
③ 找最小不平衡子树(第一个找到的不平衡节点), "个头"(子树高度) 最高的儿子, 孙子
④ 根据孙子位置, 调整平衡
孙子在LL, 儿子右单旋
孙子在RR, 儿子左单旋
孙子在LR, 孙子先左旋, 再右旋
孙子在RL, 孙子先右旋, 再左旋
⑤ 删除之后可能导致原本树高减少,翻转之后又可能导致树变矮,所以不平衡可能会传递。
继续②
需要频繁转换形态, 引入红黑树
红黑树(RBT)
-
定义
红黑树是满足以下性质的二叉排序树
①每个结点或是红色,或是黑色的
②根节点是黑色的
③叶结点(外部结点、NULL结点、失败结点)均是黑色的
④不存在两个相邻的红结点(即红结点的父节点和孩子结点均是黑色)
⑤对每个结点,从该节点到任一叶结点的简单路径上,所含黑结点的数目相同左根右, 根叶黑
不红红, 黑路同struct RBNode { int key; // 关键字的值 RBNode *parent; // 父节点指针 RBNode *LChild; // 左孩子指针 RBNode *RChild; // 右孩子指针 int color; // 节点颜色 }; -
性质
- 从根节点到叶结点的最长路径 ≤ 2 * 最短路径
- 有n个内部节点的红黑树高度 $h ≤ 2log_2(n+1)$
节点数最少 $2^h-1$ , 最多$2^h + 1$
-
插入

-
删除
时复$O(log_2n)$
处理方式与二叉排序树一样
B树
-
定义
m阶b树是所有节点平衡因子均等于0的m路平衡查找树 -
性质
根节点的子树数 ∈[2, m], 关键字数∈[1, m-1]

$$
log_m(n + 1) ≤ h ≤ log_(m/2)(n + 1)/2 + 1
$$
-
插入
插入时, 如果插入后的关键字数 > m - 1就需要拆开, 将[m / 2] -1 的点往上提, 左半部分不动, 右半部分变到刚往上提的节点下 -
删除
1) 删除后的关键字 $≥ \lceil m / 2 \rceil$, 则能直接删除
2) 借兄弟, 父子换位法, 将当前节点的父节点拿下来当儿子, 其后继的后继节点上去当父亲
3) 兄弟不够借, 将关键字删除后, 与兄弟节点和双亲节点的关键字合并 -
B+树

散列表
可以根据数据元素的关键字计算出它在散列表中的存储地址
哈希函数: 建立了"关键字" -> "存储地址"的关系
-
构造
① 除留余数法
取一个 <= 表长m 的质数p
$$
H(key) = key % p
$$
② 数字分析法 -
处理冲突
- 拉链法
将所有的同义词放在一个线性链表中 - 开放地址法
发生冲突后给新元素找一个新的位置, 一个散列地址既向它的同义词开放, 又向它的非同义词开放
$$
H_i = (H(key) + d_i) % m
$$
确定 $d_i$
① 线性探测法
② 平方探测法
③ 双散列法
④ 伪随机序列法
- 拉链法
排序
讲解
| 算法 | 最好情况 | 最坏情况 | 平均情况 | 空间复杂度 | 稳定性 |
|---|---|---|---|---|---|
| 直接插入排序 | O(n) | O(n2) | O(n2) | O(1) | 稳定 |
| 冒泡排序 | O(n) | O(n2) | O(n2) | O(1) | 稳定 |
| 简单选择排序 | O(n2) | O(n2) | O(n2) | O(1) | 不稳定 |
| 希尔排序 | O(1) | 不稳定 | |||
| 快速排序 | O(nlog2n) | O(n2) | O(nlog2n) | O(log2n) | 不稳定 |
| 堆排序 | O(nlog2n) | O(nlog2n) | O(nlog2n) | O(1) | 不稳定 |
| 二路归并排序 | O(nlog2n) | O(nlog2n) | O(nlog2n) | O(n) | 稳定 |
| 基数排序 | O(d(n+r)) | O(d(n+r)) | O(d(n+r)) | O(r) | 稳定 |
/**
* 插入排序
*/
void InsertSort(int a[], int n);
void ShellSort(int A[], int n);
/**
*交换排序
*/void BubbleSort(int a[], int n);
int Partition(int a[], int low, int high);
void QuickSort(int a[], int low, int high);
/**
* 选择排序
*/void SelectSort(int a[], int n);
void HeapAdjust(int a[], int k, int len);
void BuildMaxHeap(int a[], int n);
void HeapSort(int a[], int n);
/**
* 其他
*/// 归并排序
void Merge(int a[], int low, int mid, int high);
void MergeSort(int a[], int low, int high);
插入排序
将待排序记录的关键字按其大小插入到前面已经排序好的子序列中
直接插入
| 空间效率 | $O(1)$ |
|---|---|
| 时间复杂度 | $O(n^2)$ |
| 稳定 | |
| 顺序存储和链式存储的线性表 |
void InsertSort(int a[], int n) {
int i, j, temp;
for (i = 1; i < n; i++) {
if (a[i] < a[i - 1]) {
temp = a[i];
for (j = i - 1; j > 0 && a[j] > temp; --j)
a[j + 1] = a[j];
a[j + 1] = temp;
}
}
}
折半插入
用折半查找找到应该插入的位置, 再移动元素
直到$low > high$ 才停止查找
若$a[mid] == 查找元素$ , 继续令$low = mid + 1$, 保持稳定性, 最终将元素插入到low所指位置, 即$(high + 1)$
| 空间效率 | $O(1)$ |
|---|---|
| 时间复杂度 | $O(n^2)$ |
| 稳定 | |
| 顺序存储的线性表 |
希尔排序
先将待排序表分为若干$L[i, i+d, i+2d... i+kd]$的形式, 对各个子表分别进行直接插入排序, 缩小增量d, 重复直至1
| 空间效率 | $O(1)$ |
|---|---|
| 时间复杂度 | 最坏$O(n^2)$ |
| 不稳定 | |
| 顺序存储的线性表 |
void ShellSort(int A[], int n) {
int d, i, j;
for (d = n / 2; d >=1; d = d / 2) {
for (i = d + 1; i <= n; ++i) {
if (A[i] < A[i -d ]) {
A[0] = A[i -d];
for (j = i - d; j > 0 && A[0] < A[j]; j -=d)
A[j + d] = A[j];
A[j + d] = A[0];
}
}
}
}
交换排序
冒泡排序
比较次数 $n(n - 1)/2$
移动次数$3n(n - 1) / 2$
| 空间效率 | $O(1)$ |
|---|---|
| 时间效率 | 最好$O(n)$ 最坏$O(n2)$<br>平均$O(n2)$ |
| 稳定 | |
| 顺序和链式存储的线性表 |
快速排序
任取一个元素pivot 作为基准(通常首元素), 通过一趟排序将表划分为独立的两部分, 左边更小, 右边更大, 则pivot的最终位置确定在L(k)上, 分别递归对两个子表调用, 直至每部分只有一个元素或为空
int Partition(int a[], int low, int high) {
int pivot = a[low];
while (low < high) {
while (a[high] >= pivot)
high--;
a[low] = a[high];
while (a[low] < pivot)
low++;
a[high] = a[low];
}
a[low] = pivot;
return low;
}
void QuickSort(int a[], int low, int high) {
if (low < high){
int pivotPos = Partition(a, low, high);
QuickSort(a, low, pivotPos -1);
QuickSort(a, pivotPos + 1, high);
}
}
| 时复 | $O(n * 递归层数)$ 最好$O(n * log_2n)$ 最差$O(n^2)$ |
|---|---|
| 空复 | O(递归层数) 最好$O(log_2n)$ 最差$O(n)$ |
| 不稳定 | |
| 顺序存储的线性表 |
选择排序
每一趟在待排序元素中选取关键字最小的元素加入有序子序列
简单选择
void SelectSort(int a[], int n) {
for (int i = 0; i < n -1; i++) {
int min = i;
for (int j = i + 1; j < n; j++) {
if (a[j] < a[min])
min = j;
}
if (min != i)
swap(a[i], a[min]);
}
}
| 时复 | $O(n^2)$ |
|---|---|
| 空复 | O(1) |
| 不稳定 | |
| 顺序表, 链表都可以 | 以及关键字较少的情况 |
堆
大根堆: 完全二叉树中, 根 ≥ 左右
小根堆: 完全二叉树中, 根≤ 左右
建立大根堆:
把所有非终端结点都检查一遍,
检查当前节点是否满足 根 ≥ 左右, 不满足就将当前节点与更大的一个孩子互换
若互换破坏了下一级的堆, 就采用相同的方法继续向下调整(小元素不断下坠)
堆排序: 每一趟将堆顶元素与待排序序列的最后一个元素交换, 并将待排序元素序列 再次调整为大根堆,小元素不断下坠, 重复n-1趟
插入: 对于小根堆, 新元素放在表尾, 与父节点相比, 若新元素更小, 则交换, 一路北伐
删除: 被删除的元素用堆底的元素替代, 让其不断下坠
// 以k为根的子树调整为大根堆
void HeapAdjust(int a[], int k, int len) {
// a[0]暂存子树的根节点
// k为正在筛选的有可能不断下坠的节点
a[0] = a[k];
// 沿key较大的的子节点向下筛选
for (int i = 2 * k; i <= len; i *= 2) {
// i < len保证当前节点有右兄弟
if (i < len && a[i] < a[i + 1])
i++; // 取key较大的子节点的下标
// 筛选结束
if (a[0] >= a[i])
break;
// a[i] 调整到双亲节点
a[k] = a[i];
// 继续向下筛选
k = i;
}
// 被筛选的节点的值放入最终位置
a[k] = a[0];
}
// 建立大根堆
void BuildMaxHeap(int a[], int n) {
for (int i = n / 2; i >= 1; i--) {
HeapAdjust(a, i, n);
}
}
// 排序
void HeapSort(int a[], int n) {
BuildMaxHeap(a, n);
// n-1趟的交换和建堆过程
for (int i = n; i > 1; i--) {
// 交换堆顶和堆底元素
swap(a[1], a[i]);
// 剩余待排序元素调整为堆
HeapAdjust(a, 1, i - 1);
}
}
一个节点, 每下坠一层, 最多只需对比关键字2次
若树高h, 某节点在第i层, 则将这个节点向下调整最多只需要下坠$h-i$层, 关键字对比次数不超过$2(h - i)$
建堆过程中, 对比次数不超过$4n$, 时复$O(n)$
排序过程中, 根节点最多下坠h-1层
每一趟排序复杂度不超过$O(h) = O(log_2n)$
共n-1趟, 总的时间复杂度$O(nlog_2n)$
堆排序时复: $O(n) + O(nlog_2n)$ = $O(nlog_2n)$
| 时复 | 建堆$O(n)$ 排序$O(nlogn)$ 总$O(nlogn)$ |
|---|---|
| 空复 | O(1) |
| 不稳定 | |
| 顺序表 |
归并, 基数, 计数
归并
把两个或多个已经有序的序列合并成一个
m路归并, 每选出一个元素需要对比关键字m-1次
// 辅助数组
int *b = (int *) malloc(n * sizeof(int));
// a[low....mid]和 a[mid+1...high]各自有序
void Merge(int a[], int low, int mid, int high) {
int i, j ,k;
// a中所有元素复制到b中
for (k = low; k <= high; k++)
b[k] = a[k];
// 将较小值复制到a中
for (i = low, j = mid + 1; i <=mid && j <= high; k++) {
if (b[i] <= b[j]) //两个元素相等时, 优先使用靠前的, 保证稳定性
a[k] = b[i++];
else
a[k] = b[j++];
}
// 没有归并完的部分复制到尾部
while (i <= mid)
a[k++] = b[i++];
while (j <= high)
a[k++] = b[j++];
}
void MergeSort(int a[], int low, int high) {
if (low < high) {
// 从中间划分
int mid = (low + high) / 2;
// 对左半部分归并
MergeSort(a, low, mid);
// 对右半部分归并
MergeSort(a, mid + 1, high);
// 归并
Merge(a, low, mid, high);
}
}
| 空间效率 | $O(n)$ |
|---|---|
| 时间复杂度 | $O(nlogn)$ |
| 稳定 | |
| 顺序和链式存储 |
基数
基于关键字各位的大小
百位相同, 按十位递减, 十位相同按个位递减
r: 各关键字位数有可能取到的个数, r个辅助队列
d元组
| 空间效率 | $O(r)$ |
|---|---|
| 时间复杂度 | $O(d(n+r))$ |
| 稳定 | |
| 顺序和链式存储 |
一趟分配O(n), 一趟收集O(r), 总共d趟分配, 收集, 总时间复杂度= $O(d(n+r))$
适用
①数据元素的关键字可以方便地拆分为d组,且d较小
②每组关键字的取值范围不大,即r较小
③数据元素个数 n 较大
计数
对每个待排序的元素x, 统计 $<x$ 的元素个数
外部排序
若要进行k路归并排序,则需要在内存中分配k个输入缓冲区和1个输出缓冲区
①生成 个初始归并段(对L个记录进行内部排序,组成一个有序的初始归并段)
步骤
②进行 S趟k路归并,$S= \lceil log_kr \rceil$
外部排序时间开销 = 读写外存的时间 + 内部排序的时间 + 内部归并的时间
采用多路归并可以减少归并趟数, 从而减少IO次数
对r个初始归并段, 做k路归并, 则归并树可用k叉树表示
若树高为h, 则 $归并趟数 = h - 1 = \lceil log_kr \rceil$
k叉树的第h层最多有$k^h-1$个结点
则 r ≤ k^(h-1), (h-1)最小 = $\lceil log_kr \rceil$
k越大, r越小, 归并趟数越少, IO越少
优化1: 增加k,
代价1, 需要增加相应的输入缓冲区
代价2, 每次从k个归并段中选一个最小元素需要(k-1)次对比 ----败者树减少
优化2: 减少r
若共有N个记录, 内存工作区可以容纳L个记录, 则初始归并段数量 r = N / L --- 置换选择排序减少r
败者树
使用多路平衡归并可以减少归并趟数,但笨方法从k个归并段选一个最值需要进行k-1次比较, 有了败者树后, 选出最小元素, 只需对比 $\lceil log_2k \rceil$.
可视为一颗完全二叉树, k个叶节点分别是当前参与比较的元素, 非叶结点用来记忆子树中的失败者, 胜者往上比较, 直到根节点
置换-选择

最佳归并树
归并过程中 IO次数 = 2 * 归并树WPL
哈夫曼树的思想推广到m叉树
如果初始归并段的数量无法构成严格的k叉归并树(树中只包含度为k, 度为0的点), 则需补充几个长度为0的虚段
初始归并段数量 + 虚段数量 = $n_0$
$$
n_k = (n_0 -1) / (k- 1)
$$
- (初始归并段数量 - 1) % (k - 1) = 0,则能构成完全k叉树
- (初始归并段数量 - 1) % (k - 1)= u ≠ 0,则说明需要添加(k - 1)- u 个虚段才能构成完全二叉树


 浙公网安备 33010602011771号
浙公网安备 33010602011771号