KMP

KMP 算法

KMP 算法是单模匹配算法，即在一个长度为 n 的文本串中查找一个长度为 m 的模式串。它的复杂度是 \(O(n+m)\)，差不多是此类算法能达到的最优复杂度。朴素的模式匹配算法（暴力方法）: 在S的所有字符中逐个匹配 P 的每个字符。

结论：朴素算法在某种特殊字符串（比如例1）中，复杂度差不多 \(O(n+m)\)， 这已经是字符串匹配能达到的最优复杂度了。所以，如果字符串S,P符合这个特征，用暴力法是不错的选择。但是，如果情况比较坏（比如例2），那么复杂度就退化成 \(O(nm)\)。
KMP算法是一种在任何情况下都能达到 \(O(n+m)\) 复杂度的算法。它是通过分析 P 的特征对 P 进行预处理，从而在与 S 匹配的时候能够跳过一个字符串，达到快速匹配的目的。

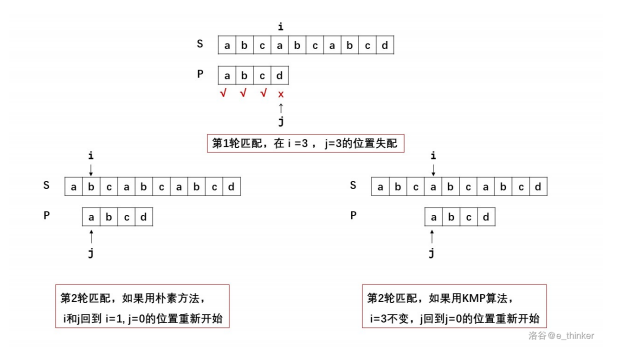
在用 KMP 算法时，指向 S 的 I 指针不会回溯，而是一直往后走到底。与朴素算法相比，大大减少了匹配次数。那么 KMP 是如何让 i 不回溯，只回溯 j 的呢？这就是 KMP 的核心—— next[] 数组。当出现失配后，进行下一次匹配时，用 next[] 指出 j 回溯的位置。
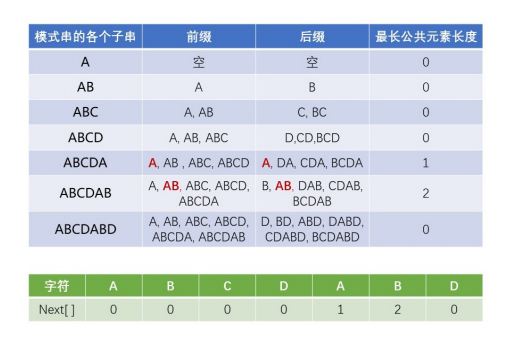
如果给定的模式串是：“ABCDABD”，从左至右遍历整个模式串，其各个子串的前缀后缀分别如下表格所示：

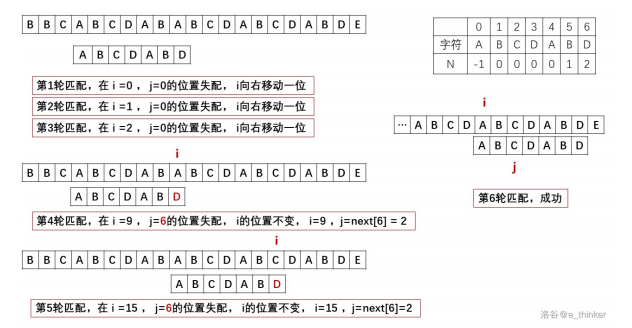
以下是 P3375 的参考答案

#include<bits/stdc++.h>
using namespace std;
typedef unsigned long long qaq;
const int N=1000010;
int nxt[N];//nxt好东西
char t[N],p[N];//文本串和子串
int tl,pl,j;//tl pl 分别为文本串和子串的长度 
int i;
int main() {
	cin>>(t+1)>>(p+1);//注意这里输入后下标从1开始
	tl=strlen(t+1);//t的长度
	pl=strlen(p+1);//p的长度
	//接下来是计算nxt数组
	for(i=2;i<=pl;i++)
		//例如子串ABCDABD 在i=5时j为1 因为找到了与第一个字母相同的字母
		//然后i=6时j=2，因为在第一个字符之后连续找到了一样的字母
		//这样就可以求出 最长的公共子序列为AB 长度为2 （就是被存入nxt[]的j的值
		//哦~（恍然大悟 
	{
		while(j&&p[i]!=p[j+1])//结果：j为0或两个字符相等  【只要判断j为0这一轮j就不会改变】 
		j=nxt[j];
		if(p[j+1]==p[i])j++;//如果是两个字符相等则j++
		nxt[i]=j;
	}
	j=0;//在这里j充当计数的角色
		//即记录已判断字符数量 
	//KMP来啦
	for(i=1;i<=tl;i++){//i表文本串现在位置 
		while(j>0&&p[j+1]!=t[i])j=nxt[j];//判断不一致就卡 
		if(p[j+1]==t[i])j++;// 若判断一致则判断下一个
		if(j==pl)//判断完成
		{
			cout<<i-pl+1<<endl;//在文本串中的位置
			j=nxt[j]; 
		} 
	} 
	
	//一般来说做到这里就结束了 但题目有说要打印nxt数组 
	for(i=1;i<=pl;i++)
	cout<<nxt[i]<<" ";
	
	
	return 0;
}