R1

T3(P4694 [PA 2013] Raper)

一道模拟费用流入门题。

重温一下网络流，EK/Dinic 到底是在干什么？
相比于 FF 的区别就在于，后者每次总是找的是 \(S \to T\) 的长度最小的的增广路。需要指出的是，这样找增广路的话，下一次的增广路长度永远大于等于这一次的增广路。考虑一次增广对最短路的影响，实际上是把那些瓶颈边的正向边全部删掉，经过的所有反向边加上（或者可能原本就有），而对于其余的边没有影响。考察新加进来的这些边能否使得最短路长度变小，画一下就会发现经过反向边的增广路一定大于等于本次增广的增广路。
我们在 Dinic 时，实际上每次多路增广就是把长度为本次最短路 \(d\) 的所有增广路全部增广一遍。因为长度为 \(d\) 的不同增广路至多 \(m\) 条，因为各个增广路的瓶颈不能有交集，否则就有一条肯定走不了了，而每次增广至多经过 \(n\) 个点，这样多路增广一次是 \(O(nm)\)。而长度 \(d\) 取遍 \([1,n] \cap \mathbb{Z}\)，总的复杂度就是 \(O(n^2m)\)。突然发现这个时间复杂度怎么来的还是很有必要了解一下的。
发动人类智慧，感性理解一下，只要没有负环，费用流模型也有类似的性质，即如果我们每次都增广最短的那个的话，下一次增广出的一定比现在这个长（或者等于）。这说明，最小费用关于流下凸。
对于费用流问题的 SSP 算法。由于我们每次增广最短路，这样每次得到的都是当前最小费用流，我们再明确一下流量为 \(i\) 的最小费用流总是来自 \(i - 1\) 的最小费用流（因为你从 \(i - 2\) 增广两次不就相当于先到 \(i - 1\) 吗），然后我们在说明一下长度相同的那些增广路的增广顺序是无所谓的（因为上面那个瓶颈的性质），这样就可以说明正确性了。

让我们回到模拟费用流。我曾多次听闻反悔贪心都有其对应的模拟费用流模型，至少在本题来说是这样。那么直接说是反悔贪心就行了呗，干嘛还要有模拟费用流这种东西呢。至少做完这道题之后，可以粗略地认为，费用流模型的作用有两个，一是说明凸性，二是方便分析。
这题的费用流建模如下：
\(S \to S'\)，容量为 \(k\)，代价为 \(0\)。
\(S' \to a_i\)，容量为 \(1\)，代价为 \(a_i\)。
\(a_i \to b_j(\forall i \le j)\)，容量为 \(1\)，代价为 \(0\)。
\(b_i \to T\)，容量为 \(1\)，代价为 \(0\)。
这说明，答案关于制作的光盘数下凸。

那么就可以 wqs 二分把 \(k\) 的限制给去掉了。

让我们先重温一下 wqs 二分。

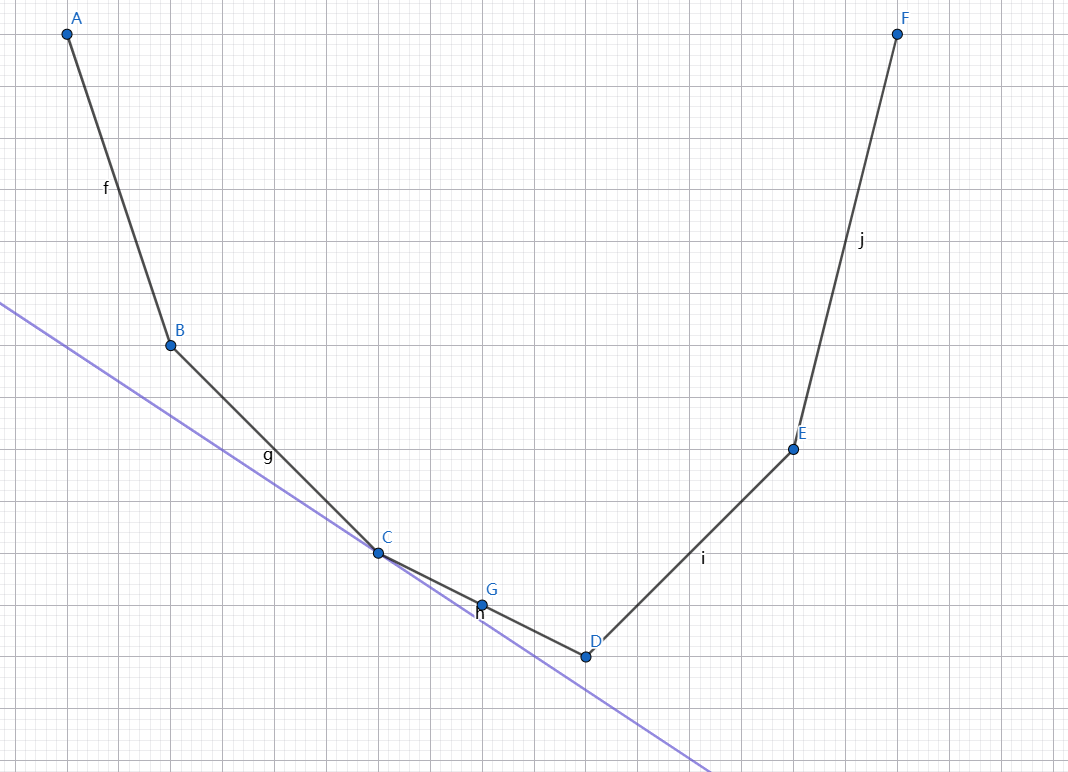
对于这样一个凸包，我们考虑用斜率为 \(k\) 的直线来切它。由于凸性，当 \(k\) 递增时，切点一定不断右移。假设我们此时切到的 \(C\) 点是 \((i, f(i))\)，那么这条直线就是 \(y = kx + (f(i) - ki)\)。根据斜率优化的知识，我们知道 \(k\) 固定时相切截距最小，也就是要最小化 \(f(i) - ki\)。