模拟赛 R15
R15 - 我想不出有趣的题目名称了所以这题就叫排列
题意
给定一个正整数 \(n\) 以及一个长度为 \(m\) 的序列 \(X\)。你需要求出有多少 \(1,2,\cdots,n\) 的排列 \(P_1,P_2,\cdots ,P_n\) 满足:该排列的所有长度为 \(m\) 的子序列中,字典序最小的是序列 \(X\)。
答案对 \(998244353\) 取模。
Solution
非常好绿题,使我爆卡 3 小时心态爆炸全场爆 0。
做着做着发现,最难处理的总是保证子序列中各元素的相对位置。
像这种给定了一个序列,就可以考虑插入法,这样就保证了这个子序列肯定存在。然后再去看字典序的限制。
如果 \(X_i\) 递增,考虑 \(1 - n\) 中每个数插在哪里,可以进行计数,注意一些 corner-cases。
否则,找到第一个 \(i,s.t. X_i > X_{i + 1}\),可以发现最终序列中的最后 \(m - i\) 位一定是 \(X_{i + 1}X_{i + 2}...X_m\),这样只需要对于前面进行相同的计数即可。
插入的想法确实没怎么见过,是我太菜了。
Code
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 3e5 + 5, mod = 998244353;
int a[N], n, m, j, pos[N];
ll ans = 1;
signed main(){
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
cin >> n >> m;
for(int i = 1; i <= m; ++i){
cin >> a[i];
}
for(int i = 1; i <= m; ++i){
pos[a[i]] = i;
if(!j && a[i] > a[i + 1]) j = i;
}
int cnt = 0;
for(int i = 1; i <= n; ++i){
if(pos[i]){
if(pos[i] <= j) ++cnt;
if(pos[i] == j) ++cnt;
continue;
}
(ans *= cnt) %= mod;
cnt++;
}
cout << ans;
return 0;
}
R15 - 其实我很想在题目名称里整点活但是我连题目背景都懒得写了所以这道题叫不知道
题意
给定 \(n\times n\) 的网格,你要在上面画若干条线段,每条线段的两个端点必须是网格上的整点(坐标 \(0\sim n\))。
要求这些线段两两都不平行,且网格上的每个格子(共 \(n\times n\) 个)都被至少一条线段穿过。
一条线段穿过一个格子,当且仅当存在线段上的一个点在格子内部(不包含边界)。下图展示了一个 \(n=3\) 时的方案。
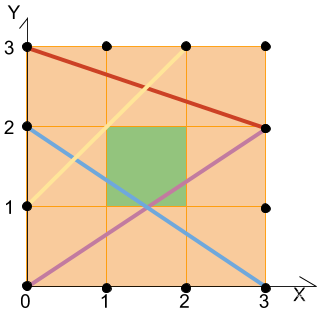
你需要画尽可能少的线段。请输出你的方案。
Solution
使用 \(n + 1\) 条线段的构造方案。
基本想法是:使得斜率为互质的是最赚的,因为每增长一格可以覆盖两个格子。
然后按这个填就行,一些 corner 注意一下,具体看题解吧,毕竟构造题我也不太可能做出来。
Code
#include <bits/stdc++.h>
using namespace std;
const int N = 1e3 + 5;
void solve(){
int n;
cin >> n;
if(n == 1) return cout << 1 << '\n' << 0 << ' ' << 0 << ' ' << 1 << ' ' << 1 << '\n', void();
cout << n + 1 << '\n';
for(int i = 0, j = n - 1; j > 0; i += 2, j -= 2){
cout << i << ' ' << 0 << ' ' << n << ' ' << j << '\n';
}
for(int i = 1, j = n - 2; j > 0; i += 2, j -= 2){
cout << 0 << ' ' << i << ' ' << j << ' ' << n << '\n';
}
cout << 0 << ' ' << n << ' ' << n << ' ' << n - 1 << '\n';
cout << n - 1 << ' ' << n << ' ' << n << ' ' << 0 << '\n';
}
signed main(){
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
int T;
cin >> T;
while(T--) solve();
return 0;
}
R15 - 凸多边形必须是凸的,此乃亘古不变之真理
题意
给定两个长度为 \(n\) 的整数序列 \(x_1,x_2,\cdots,x_n\) 和 \(y_1,y_2,\cdots,y_n\)。
对于一个长度为 \(n\) 的排列 \(p_1,p_2,\cdots,p_n\),在二维平面上有以下 \(n\) 个点 \((x_1,y_{p_1}),(x_2,y_{p_2}),\cdots,(x_n,y_{p_n})\),你需要找到一个面积最小(可能为 \(0\))的凸多边形,使得这 \(n\) 个点都在凸多边形的内部(在边和顶点上也算在内部)。
对所有可能的排列,你都需要找到这样的凸多边形。你需要求出这些凸多边形的面积之和。
你需要输出答案对 \(998244353\) 取模后的结果。
Solution
Shoelace Formula:对于任意一个 \(n(n \ge 3)\) 边形,假设其顶点按逆时针为 \(P_1P_2\cdots P_n\),那么该多边形的面积为 \(\sum_{i = 1}^n P_i \times P_{i + 1}\),规定 \(P_{n+1} = P_1\)。
叉积的性质把容斥直接凑好了,可以感性理解一下。
那么在本题中,我们可以先 \(O(N^4)\) 的枚举可能的点对 \((A, B)\),然后看 \(\vec{AB}\)(注意是有向的)在多少个凸包中出现,按这个系数把 \(A \times B\) 贡献到答案。
\(\vec{AB}\) 在凸包上等价于所有的点都在他的上方(或者说左侧),由于是线性的,可以考虑从小到大(从大到小)的每个 \(x_i\) 能与哪些 \(y_j\) 匹配,乘法原理计数。
一个细节,如果一个 \(A_{x} < x_i < B_{x}\) 那么他在选的时候可以取到直线上,否则不行。因为我们只让共线时最两侧的点计数一次才不会算重。
卡常,注意精度。
Code
#include <bits/stdc++.h>
using namespace std;
#define int long long
typedef long double ldb;
const ldb eps = 1e-9, delta = 1e-5;
const int N = 55, mod = 998244353, inv2 = 499122177;
ldb x[N], y[N];
int n;
int ans = 0;
struct line{
ldb k, b;
inline void assign(ldb lx, ldb rx, ldb ly, ldb ry){
k = 1. * (ry - ly) / (rx - lx), b = -k * lx + ly;
}
inline ldb operator()(ldb x){
return k * x + b;
}
}l;
inline int cross(int lx, int ly, int rx, int ry){
return (lx * ry % mod - rx * ly % mod);
}
inline int sig(ldb x){
if(fabs(x) < eps) return 0;
return x < 0 ? -1 : 1;
}
signed main(){
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
cin >> n;
for(int i = 1; i <= n; ++i) cin >> x[i];
for(int i = 1; i <= n; ++i) cin >> y[i];
for(int lx = 1; lx <= n; ++lx){
for(int rx = lx + 1; rx <= n; ++rx){
for(int i = 1; i <= n; ++i){
for(int j = 1; j <= n; ++j){
if(i != j){
l.assign(x[lx], x[rx], y[i], y[j]);
int tmp1 = 1, tmp2 = 1;
if(y[i] < y[j]){
int t = 0;
for(int k = 1; k <= n; ++k){
if(k == lx || k == rx) continue;
while(t < n && sig(y[t + 1] - l(x[k]) - delta * (k > lx && k < rx)) < 0) ++t;
(tmp1 *= (t - (k - 1))) %= mod;
if(tmp1 == 0) break;
}
t = n + 1;
for(int k = n; k >= 1; --k){
if(k == lx || k == rx) continue;
while(t > 1 && sig(y[t - 1] - l(x[k]) + delta * (k > lx && k < rx)) > 0) --t;
(tmp2 *= ((n - t + 1) - (n - k))) %= mod;
if(tmp2 == 0) break;
}
}
else{
int t = 0;
for(int k = n; k >= 1; --k){
if(k == lx || k == rx) continue;
while(t < n && sig(y[t + 1] - l(x[k]) - delta * (k > lx && k < rx)) < 0) ++t;
(tmp1 *= (t - (n - k))) %= mod;
if(tmp1 == 0) break;
}
t = n + 1;
for(int k = 1; k <= n; ++k){
if(k == lx || k == rx) continue;
while(t > 1 && sig(y[t - 1] - l(x[k]) + delta * (k > lx && k < rx)) > 0) --t;
(tmp2 *= ((n - t + 1) - (k - 1))) %= mod;
if(tmp2 == 0) break;
}
}
(ans += tmp1 * cross(x[lx], y[i], x[rx], y[j]) + tmp2 * cross(x[rx], y[j], x[lx], y[i])) %= mod;
}
}
}
}
}
cout << (-ans) * inv2 % mod;
return 0;
}
R15 - Ἄρτεμις
题意
称一个 01 串是好的,当且仅当该串的任意一个前缀子串满足 1 的个数不少于 0 的个数,任意一个后缀子串也满足 1 的个数不少于 0 的个数。
给定一个长度为 \(n\) 的 01 串(下标从 \(1\) 开始)和 \(m\) 个操作,每个操作有以下两种:
1 l r,你需要在下标区间 \([l,r]\) 内选出一个最长的子序列,使得这个子序列拼成的串是好的。你只需要求出它的长度。2 x,你需要修改下标为 \(x\) 的字符,把 0 变成 1,把 1 变成 0。
Solution
先考虑单次询问怎么做。把 0 看成 -1,1 看成 1,\(a\) 是前缀和,\(b\) 是后缀和。这个子序列的长度就是总数减去删掉 -1 的个数。
先满足前缀的要求,贪心地,遇到一个 0,并且发现前面 1 的个数小于 0 了,那就把这个 0 删掉,发现这样的代价是 \(\max_{i = 1}^n\{-a_i\}\)。
由于第一步中我们总是删掉最后的,那么这样对于后缀和是最有利的。如果把删掉的那一位数值看成 0,那么做完第一步之后,新的后缀和 \(b'_i = b_i + \max_{j = 1}^n\{-a_j\} - \max_{j = 1} ^{i - 1}\{-a_j\}\)。
那么总的代价是 \(\max_{i = 1}^n\{-a_i\} + \max_{i = 1}^n\{-b_i - \max_{j = 1}^n\{-a_j\} + \max_{j = 1} ^{i - 1}\{-a_j\} \}\)。然后可以推式子,先把后面那个 max 里面的常量提出来,发现跟第一项消掉了,所以要求的就是 \(\max_{i = 1}^n\{-b_i + \max_{j = 1} ^{i - 1}\{-a_j\}\)。后面跟这道题的过程很像,都是先把 max 丢了,变成 \(\max_{1 \le i \le j \le n}\{-b_i-a_j\}\)。那道题到这里就可以维护了,但由于我们这里还有区间查询,询问与询问之间的 \(a\) 和 \(b\) 不相同,把前缀和拆了会很丑。不过到这里多想一步就可以了,负号提出来 \(-\min_{1 \le i \le j \le n}\{b_i + a_j\}\),发现是要两边的和最小。那不就是区间和减去最大子段和吗。维护最大子段和即可。
特判区间内全是 0 的情况。
Code
#include <bits/stdc++.h>
using namespace std;
const int N = 6e5 + 5;
int n, m;
bitset<N> bs;
struct node{
int sum, lp, rp, ans;
}tr[N << 2];
#define ls(p) p << 1
#define rs(p) p << 1 | 1
#define cvt(x) (x ? 1 : -1)
node merge(node x, node y){
return node{x.sum + y.sum, max(x.lp, x.sum + y.lp),
max(y.rp, y.sum + x.rp), max({x.ans, y.ans, x.rp + y.lp})};
}
void update(int p, int pl, int pr, int x, int k){
if(pl == pr) return tr[p] = node{k, k, k, k}, void();
int mid = (pl + pr) >> 1;
if(x <= mid) update(ls(p), pl, mid, x, k);
else update(rs(p), mid + 1, pr, x, k);
tr[p] = merge(tr[ls(p)], tr[rs(p)]);
}
node query(int p, int pl, int pr, int L, int R){
if(L <= pl && R >= pr) return tr[p];
int mid = (pl + pr) >> 1;
if(L <= mid && R > mid) return merge(query(ls(p), pl, mid, L, R), query(rs(p), mid + 1, pr, L, R));
if(L <= mid) return query(ls(p), pl, mid, L, R);
if(R > mid) return query(rs(p), mid + 1, pr, L, R);
}
signed main(){
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
cin >> n >> m;
for(int i = 1; i <= n; ++i){
char x; cin >> x;
if(x - '0') bs[i] = 1;
update(1, 1, n, i, cvt(bs[i]));
}
while(m--){
int op;
cin >> op;
if(op == 1){
int l, r;
cin >> l >> r;
node t = query(1, 1, n, l, r);
if(t.sum == -(r - l + 1)) cout << 0 << '\n';
else cout << (r - l + 1) + t.sum - t.ans << '\n';
}
else{
int pos; cin >> pos;
bs.flip(pos);
update(1, 1, n, pos, cvt(bs[pos]));
}
}
return 0;
}
Summary
不要炸心态啊,不会就跳,不要吃压力。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号