BZOJ 杂题选记(9.7 - 9.13)
P5909 挂坠
经典贪心:\(n\) 个任务,有时长 \(w_i\) 和必须在 \(c_i\) 之前开始的限制,求最多能完成几个任务。
交换邻项,可得策略按 \(w_i + c_i\) 从小到大排序。然后在按重量反悔贪心,发现两问一起解决了。
Code
#include <bits/stdc++.h>
using namespace std;
const int N = 2e5 + 5;
typedef long long ll;
int n;
struct node{
ll w, c, r;
}a[N];
priority_queue<ll> q;
signed main(){
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
cin >> n;
for(int i = 1; i <= n; ++i) cin >> a[i].c >> a[i].w, a[i].r = a[i].w + a[i].c;
sort(a + 1, a + 1 + n, [](node x, node y){ return (x.r == y.r ? x.w < y.w : x.r < y.r); });
ll sum = 0, ans = 0;
for(int i = 1; i <= n; ++i){
if(sum <= a[i].c){
++ans;
q.push(a[i].w);
sum += a[i].w;
}
else{
if(a[i].w < q.top()){
sum += -q.top() + a[i].w;
q.pop();
q.push(a[i].w);
}
}
}
cout << ans << '\n' << sum << '\n';
return 0;
}
P3620 数据备份
经典贪心:在 \(n\) 个数中选出 \(k\) 个不相邻的使得总和最小。
一个很 tricky 的策略,类似网络流退流的感觉,就是选了一个数 \(i\) 之后,删除左右两个数 \(l_i\),\(r_i\),并把 \(val_i \gets val_{l_i} + val{r_i} - val_{i}\) 重新丢进小根堆,每次选最小的。注意需要用链表维护邻项,因为可能出现二次反悔的情况。
Code
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 5;
typedef long long ll;
typedef pair<ll, int> pii;
int a[N], n, k, pre[N], nxt[N];
ll ans, val[N];
bitset<N> bk;
priority_queue<pii, vector<pii>, greater<pii> > q;
void del(int x){
nxt[pre[x]] = nxt[x];
pre[nxt[x]] = pre[x];
bk[x] = 1;
}
signed main(){
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
cin >> n >> k;
for(int i = 1; i <= n; ++i){
cin >> a[i];
pre[i] = i - 1, nxt[i] = i + 1;
val[i] = a[i] - a[i - 1];
if(i >= 2) q.emplace(val[i], i);
}
val[1] = val[n + 1] = 1e18;
for(int i = 1; i <= k; ++i){
while(bk[q.top().second]) q.pop();
auto [dis, u] = q.top();
q.pop();
ans += dis;
val[u] = val[pre[u]] + val[nxt[u]] - val[u];
del(pre[u]), del(nxt[u]);
q.emplace(val[u], u);
}
cout << ans;
return 0;
}
P4548 歌唱王国
概率生成函数:若 \(X\) 为仅取非负整数值的随机变量,那么 \(F_X(z) = \sum_k \operatorname{Pr}(X = k) z ^ k\)。
有结论:\(E(X) = \sum_k \operatorname{Pr}(X = k) \times k = \sum_k \operatorname{Pr}(X = k) \times k \times 1 ^ {k-1} = F'_X(1)\),一个推广 \(E(X^{\underline k}) = F^{(k)}_X(1)\)。
而又由于期望的线性性 \(D(X) = E((X-E(X))^2) = E(X ^ 2 - 2E(X)X + E(X) ^ 2) = E(X^2) - 2E(X) \times E(X) + E(X)^2 = E(X^2) - E(X)^2\) 那么也是可以通过普通幂转下降幂类似求出的。
本题中随机变量 \(Y\) 表示序列停止时的长度,那么可以定义 \(f_i = \operatorname{Pr}(i = Y)\)。那么 \(E(Y) = F_Y'(1)\)。一个 trick,定义 \(g_i = \operatorname{Pr}(i > Y)\) 来辅助,有一个普适的结论是 \(f_{i + 1} + g_{i + 1} = g_i\) 可以推出 \(F + G = xG + 1\),这个 \(1\) 是来补齐常数项的。那么 \(F = (x-1)G + 1\),\(F' = G\),所以 \(F'(1) = G(1)\)。得出了一个类似反演的柿子。
然后就要发挥人类智慧算 \(G(1)\) 了,就看题解吧。
Code
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int mod = 1e4, N = 1e5 + 5;
int n, t, pw[N], m, a[N], nxt[N];
void solve(){
cin >> m;
for(int i = 1; i <= m; ++i) cin >> a[i];
nxt[1] = 0;
for(int i = 2; i <= m; ++i){
int j = nxt[i - 1];
while(j && a[j + 1] != a[i]) j = nxt[j];
if(a[j + 1] == a[i]) ++j;
nxt[i] = j;
}
int ans = 0;
for(int i = m; i; i = nxt[i])
(ans += pw[i]) %= mod;
cout << setw(4) << setfill('0') << ans << '\n';
}
int main(){
cin.tie(0)->sync_with_stdio(0);
cin >> n >> t;
pw[0] = 1;
for(int i = 1; i <= 1e5; ++i) (pw[i] = pw[i - 1] * n) %= mod;
while(t--) solve();
return 0;
}
P4529 切割多边形 & P4534 最优切割
两道很像的题。唯一区别在于保不保证 任意两条不相邻的边所在直线的交点在模版外。不保证就是前面这道题,有 \(O(N! \times N)\) 的模拟做法,每次切割线的长度就是求出以前所有边界线与当前切割线的交点,那么最中间两个点的距离就是切割线的长度。保证的话就有 \(O(N)\) 做法了。考虑每个顶点的两条边延伸的模版边界的长度(这个可以类似旋转卡壳的做),我们肯定只用取较小的那个。唯一需要特判的就是切不到底的情况。
后面那道题的代码。
Code
#include <bits/stdc++.h>
using namespace std;
typedef long double ldb;
const ldb eps = 5e-3;
const int N = 2e3 + 5;
#define innxt(i) ((i) == m ? 1 : (i) + 1)
#define outnxt(i) ((i) == n ? 1 : (i) + 1)
#define inpre(i) ((i) == 1 ? m : (i) - 1)
#define outpre(i) ((i) == 1 ? n : (i) - 1)
struct vec{
ldb x, y;
vec operator + (vec b){ return {x + b.x, y + b.y}; }
vec operator - (vec b){ return {x - b.x, y - b.y}; }
vec operator * (ldb k){ return {x * k, y * k}; }
}out[N], in[N];
ldb cross(vec a, vec b){ return a.x * b.y - a.y * b.x; }
ldb dot(vec a, vec b){return a.x * b.x + a.y * b.y; }
ldb dis[N][2], ans, mndis[N];
ldb len(vec x){ return sqrt(x.x * x.x + x.y * x.y); }
struct line{
vec P, v;
void assign(vec x, vec y){ P = x, v = y - x; }
}outl[N];
void prt(vec p, string s = " "){
cout << "(" << p.x << ',' << p.y << ")" << s;
}
void prtl(line t){
cout << "This is a line:"; prt(t.P), prt(t.v, "\n");
}
bool on(ldb l, ldb r, ldb x){
// cout << l << ' ' << r << ' ' << x << '\n';
return x - min(l, r) >= -eps && x - max(l, r) <= eps;
}
int inter(line x, line y, vec &ret){ //外边框,内边框,0是平行,-1是交点不在外边框上或者方向相反
ldb fen = cross(y.v, x.v);
if(fabs(fen) < eps){
if(fabs(cross(y.P - x.P, x.v)) < eps) return 0;
return -1;
}
ldb k = -cross(y.P - x.P, x.v) / cross(y.v, x.v);
ret = y.P + y.v * k;
if(k <= eps || (dot(ret - x.P, x.v) <= eps || !on(x.P.x, x.P.x + x.v.x, ret.x))) return -1;
return 1;
}
int n, m;
int main(){
cin.tie(nullptr)->sync_with_stdio(0);
cin >> n;
for(int i = 1; i <= n; ++i) cin >> out[i].x >> out[i].y;
cin >> m;
for(int i = 1; i <= m; ++i) cin >> in[i].x >> in[i].y;
// 顺时针
for(int i = 1; i <= n; ++i) outl[i].assign(out[outnxt(i)], out[i]);
int j = 1;
for(int i = m; i >= 1; --i){
line t; t.assign(in[innxt(i)], in[i]);
ans += len(in[innxt(i)] - in[i]);
vec O; int typ;
while((typ = inter(outl[j], t, O)) == -1){
j = outpre(j);
}
if(typ == 0) ans -= len(in[i] - in[innxt(i)]);
else dis[i][0] = len(O - in[i]);
}
// 逆时针
for(int i = 1; i <= n; ++i) outl[i].assign(out[i], out[outnxt(i)]);
j = 1;
for(int i = 1; i <= m; ++i){
line t; t.assign(in[inpre(i)], in[i]);
vec O; int typ;
while((typ = inter(outl[j], t, O)) == -1){
j = outnxt(j);
}
if(typ == 1) dis[i][1] = len(O - in[i]);
}
bool fl = 0;
ldb sum1 = 0;
for(int i = 1; i <= m; ++i){
for(int t : {0, 1}){
if(dis[i][t] <= dis[i][t ^ 1] + eps && dis[innxt(i)][t ^ 1] <= dis[innxt(i)][t] + eps) fl = 1;
}
mndis[i] = min(dis[i][0], dis[i][1]);
sum1 += mndis[i];
}
if(!fl){
ldb tmp = 1e18;
for(int i = 1; i <= m; ++i){
tmp = min(tmp, sum1 - mndis[i] + max(dis[i][0], dis[i][1]));
}
ans += tmp;
}
else ans += sum1;
cout << fixed << setprecision(0) << ans;
return 0;
}
P4663 魔法石
字典序要按位考虑,然后就可以数位 dp 了。然后要考虑处理翻转,一个方法是正着反着一起填,记录一下前后缀是否相等,进行合法的转移。
Code
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 65;
ll f[N][N][2][2][2], rnk;
int lim[N], n, k;
#define prt(x) cout << ((x) ? 'X' : 'I')
#define nos cout << "NO SUCH STONE"
ll solve(){
memset(f, 0, sizeof(f));
for(int u = 0; u < 2; ++u){
for(int v = u; v < 2; ++v){
if(lim[1] >= 0 && lim[1] != u) continue;
if(lim[n] >= 0 && lim[n] != v) continue;
f[1][0][(u == v)][u][v] = 1;
}
}
ll ans = 0;
for(int i = 1; i <= (n + 1) / 2; ++i) for(int j = 0; j <= k; ++j)
for(int fl : {0, 1}) for(int x : {0, 1}) for(int y : {0, 1}){
if(f[i][j][fl][x][y] == 0) continue;
if(i * 2 + 1 == n){
for(int u : {0, 1}){
if(lim[i + 1] >= 0 && lim[i + 1] != u) continue;
if(j + (u != x) + (u != y) <= k)
ans += f[i][j][fl][x][y];
}
}
else{
for(int u : {0, 1}) for(int v : {0, 1}){
if(lim[i + 1] >= 0 && lim[i + 1] != u) continue;
if(lim[n - i] >= 0 && lim[n - i] != v) continue;
if(fl && u > v) continue;
if((i + 1) * 2 == n){
if(j + (u != x) + (v != y) + (u != v) <= k)
ans += f[i][j][fl][x][y];
}
else{
f[i + 1][j + (u != x) + (v != y)][fl & (u == v)][u][v] += f[i][j][fl][x][y];
}
}
}
}
return ans;
}
int main(){
cin.tie(nullptr)->sync_with_stdio(0);
cin >> n >> k >> rnk;
if(n == 1){
if(k >= 1 || rnk > 2) nos;
else if(rnk == 0) prt(0);
else prt(1);
}
else if(n == 2){
if(k == 0){
if(rnk == 0) prt(0), prt(0);
else if(rnk == 1) prt(1), prt(1);
else nos;
}
else{
if(rnk == 0) prt(0), prt(0);
else if(rnk == 1) prt(0), prt(1);
else if(rnk == 2) prt(1), prt(1);
else nos;
}
}
else{
memset(lim, -1, sizeof(lim));
if(rnk > solve()) nos;
else{
for(int i = 1; i <= n; ++i){
lim[i] = 0;
ll ret = solve();
if(rnk > ret) rnk -= ret, lim[i] = 1;
prt(lim[i]);
}
}
}
return 0;
}
P4460 手套
有意思的最不利原则,本题的边界是两个集合刚好是全集的一个划分。两边只要挑一边再取一个就可以没满足条件。
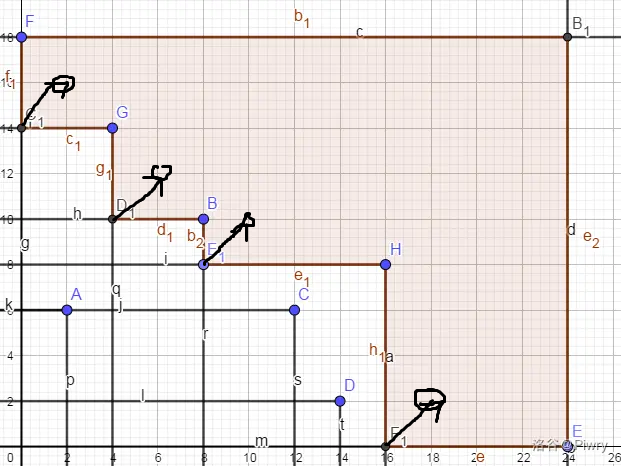
然后就按题解说的把这些凹点求出来,他们的实际含义可以这么感性理解一下:就是比如左手这边多取了一个,那么右手这边就可以少取一些,只需要保证仍然覆盖到原来的颜色就行。但是不能一直少去,当达到边界,就是凹点了。
Code
#include <bits/stdc++.h>
using namespace std;
const int N = 20;
int n, a[N], b[N], tp, st[1 << N];
struct node{
int x, y;
}p[1 << N];
int main(){
cin.tie(nullptr)->sync_with_stdio(0);
cin >> n;
for(int i = 0; i < n; ++i) cin >> a[i];
for(int i = 0; i < n; ++i) cin >> b[i];
for(int i = 0; i < (1 << n); ++i){
for(int j = 0; j < n; ++j){
if(i & (1 << j)) p[i].x += a[j];
else p[i].y += b[j];
}
}
sort(p, p + (1 << n), [](node s, node t){
return (s.x == t.x ? s.y < t.y : s.x < t.x);
});
for(int i = 0; i < (1 << n); ++i){
while(tp && p[st[tp]].y <= p[i].y) --tp;
st[++tp] = i;
}
int ans = 2e9, ansx, ansy;
for(int i = 2; i <= tp; ++i){
int sum = p[st[i - 1]].x + p[st[i]].y + 2;
if(ans > sum) ans = sum, ansx = p[st[i - 1]].x + 1, ansy = p[st[i]].y + 1;
}
cout << ansx << '\n' << ansy;
return 0;
}
P3625 采油区域
突然想起 spp 的一句话,“对于三个点和一条分界线,由于抽屉原理,那么一定是一边两个点,一边一个点。”
想到这个就可以考虑枚举分界线了,预处理两个点的情况还是 trival 的,然后把一个点和两个点的拼起来就行。
注意分解线是横着竖着都可以的,只有一个点的那边也不确定在那边,所以可以先只做分界线横着,并且一个点的那边在上面的那种情况,然后旋转着做四遍就好了。
注意旋转别写错了。
Code
#include <bits/stdc++.h>
using namespace std;
const int N = 1.5e3 + 5;
int a[N][N], n, m, k, tmp[N][N], sum[N][N], b[N][N], f[N][N], g[N][N], ans;
int getsum(int xl, int xr, int yl, int yr){
return sum[xr][yr] - sum[xl - 1][yr] - sum[xr][yl - 1] + sum[xl - 1][yl - 1];
}
void chmax(int &x, int y){ x = max(x, y); }
void solve(){
for(int i = 1; i <= n; ++i){
for(int j = 1; j <= m; ++j)
sum[i][j] = sum[i - 1][j] + sum[i][j - 1] - sum[i - 1][j - 1] + a[i][j];
}
for(int i = 1; i <= n - k + 1; ++i){
for(int j = 1; j <= m - k + 1; ++j){
b[i][j] = getsum(i, i + k - 1, j, j + k - 1);
f[i][j] = max({f[i - 1][j], f[i][j - 1], b[i][j]});
}
for(int j = m - k + 1; j >= 1; --j)
g[i][j] = max({g[i - 1][j], g[i][j + 1], b[i][j]});
}
int mx2 = -1e9;
for(int i = k + 1; i <= n - k + 1; ++i){
for(int j = 1; j <= m - k + 1; ++j){
if(j >= k) chmax(mx2, b[i - k][j] + f[i - k][j - k]);
if(j + k <= m - k + 1) chmax(mx2, b[i - k][j] + g[i - k][j + k]);
if(i - 2 * k >= 0) chmax(mx2, b[i - k][j] + f[i - 2 * k][m - k + 1]);
}
for(int j = 1; j <= m - k + 1; ++j) chmax(ans, b[i][j] + mx2);
}
}
void rotate(){
for(int j = 1; j <= m; ++j){
for(int i = 1; i <= n; ++i){
tmp[j][n - i + 1] = a[i][j];
a[i][j] = 0;
}
}
swap(n, m);
for(int i = 1; i <= n; ++i){
for(int j = 1; j <= m; ++j)
a[i][j] = tmp[i][j];
}
}
int main(){
cin.tie(nullptr)->sync_with_stdio(0);
cin >> n >> m >> k;
for(int i = 1; i <= n; ++i){
for(int j = 1; j <= m; ++j){
cin >> a[i][j];
}
}
for(int k = 0; k < 4; ++k) rotate(), solve();
cout << ans;
return 0;
}
P3626 会议中心
第一问是一个经典贪心:按右端点排序。每次找到第一个左端点大于它的线段(注意这个线段是满足条件中右端点最小的),然后一直跳就行。
发现这个可以倍增的跳,这意味着如果我们给定区间 \([l,r]\),我们可以在 \(O(\log N)\) 的时间求出只选这段内的线段最多能选多少个。
考虑按编号从小到大加入线段。一个类似估价函数的想法(不过这个估价函数是一定取得到的),如果加入第一条线段 \([l_1, r_1]\) 之后,\(ans_{1, l_1 - 1} + 1 + ans_{r_1 + 1, n}\) 就等于第一问的答案,那么就把第一条线段选上,继续类似的操作。
但是,我们还要考虑后面加入的线段不能和前面加入的线段相交,这个可以 ODT 维护。还有注意一个细节,我们后面加入的线段是要在前面已经选了一些线段的基础上还得做到最优的,所以直接查 \(ans_{1, l_i - 1} + 1 + ans_{r_i + 1, n}\) 就不对了。发现如果能找到加入线段所在那个空区间,计算空区间内答案的增量,这要就对了,依旧 ODT 维护。
这道题的倍增写法有很多细节,其一是由于线段之间严格不交,所以 \(l_i\) 要跳到 \(r_i + 1\),因此查询区间 \([l, r]\) 时,右端点要变成 \(r + 1\)。然后思考一下怎么“每次找第一个左端点大于它的线段呢”?实际上只需要加上一句话 chmin(f[i][0], f[i + 1][0]) 就行。
Code
#include <bits/stdc++.h>
using namespace std;
const int N = 2e5 + 5;
struct node{
int l, r;
mutable int v;
bool operator < (const node b) const{
return l < b.l;
}
};
typedef pair<int, int> pii;
vector<int> tmp;
int pl[N], pr[N], n, f[N * 2][21], k;
set<node> s;
int lsh(int x){
return lower_bound(tmp.begin(), tmp.end(), x) - tmp.begin() + 1;
}
int step(int st, int en){
int ret = 0;
if(st > en) return 0;
for(int i = 19; i >= 0; --i){
int nxt = f[st][i];
if(nxt <= en + 1) st = nxt, ret += (1 << i);
}
return ret;
}
void chmin(int &x, int y){ x = min(x, y); }
bool ins(int L, int R){
auto it = prev(s.upper_bound({L, R, -1}));
int pl = it -> l, pr = it -> r, v = it -> v;
if(pr >= R && v == 0){
int delta = step(pl, L - 1) + step(R + 1, pr) - step(pl, pr);
if(delta == -1){
--k;
s.erase(it);
if(pl != L) s.insert({pl, L - 1, 0});
s.insert({L, R, 1});
if(pr != R) s.insert({R + 1, pr, 0});
return 1;
}
}
return 0;
}
int main(){
cin.tie(nullptr)->sync_with_stdio(0);
cin >> n;
for(int i = 1; i <= n; ++i){
cin >> pl[i] >> pr[i];
tmp.push_back(pl[i]), tmp.push_back(pr[i]);
}
sort(tmp.begin(), tmp.end());
tmp.erase(unique(tmp.begin(), tmp.end()), tmp.end());
for(int i = 1; i <= n; ++i){
pl[i] = lsh(pl[i]), pr[i] = lsh(pr[i]);
}
int siz = tmp.size();
for(int i = 1; i <= siz + 5; ++i)
for(int j = 0; j <= 19; ++j)
f[i][j] = siz + 5;
for(int i = 1; i <= n; ++i) chmin(f[pl[i]][0], pr[i] + 1);
for(int i = siz; i >= 1; --i){
chmin(f[i][0], f[i + 1][0]);
for(int j = 1; j <= 19; ++j) chmin(f[i][j], f[f[i][j - 1]][j - 1]);
}
s.insert({1, siz, 0});
k = step(1, siz);
cout << k << '\n';
for(int i = 1; i <= n; ++i){
if(ins(pl[i], pr[i])) cout << i << ' ';
if(!k) return 0;
}
return 0;
}
P4312 OTOCI
既然是 LCT 板子,那就稍微学一下吧。
首先 LCT 只需要用到 Splay 操作和文艺平衡树的反转。LCT 维护了一颗 splay 森林来表示一颗树。每个 splay 维护的是树上的一条实链,这个 splay 森林的结构被叫做 AUX tree。splay 和 splay 之间通过虚边连接,具体来说,原树上的一条实链对应着一个 splay 的中序遍历,splay 的根向上以一条虚边连接到原树上这个链顶的父亲。一些具体的操作可以看看 oi-wiki。
基于 access 操作的 makert 的功能非常强大,它可以让原树换根。这是可以对两棵树进行连边操作的基础。
Code
#include <bits/stdc++.h>
using namespace std;
const int N = 3e4 + 5;
struct node{
int s[2], val, sum, fa, tag;
}tr[N];
#define ls(p) tr[p].s[0]
#define rs(p) tr[p].s[1]
#define val(p) tr[p].val
#define sum(p) tr[p].sum
#define fa(p) tr[p].fa
#define tag(p) tr[p].tag
#define son(p, fl) tr[p].s[fl]
bool get(int x){ return ls(fa(x)) == x ? 0 : 1; }
bool isrt(int x){ return ls(fa(x)) != x && rs(fa(x)) != x; }
void pushup(int p){ sum(p) = val(p) + sum(ls(p)) + sum(rs(p)); }
void pushdown(int p){
if(tag(p)){
swap(ls(p), rs(p));
tag(ls(p)) ^= 1, tag(rs(p)) ^= 1;
tag(p) = 0;
}
}
void update(int x){
if(!isrt(x)) update(fa(x));
pushdown(x);
}
void rotate(int x){
int y = fa(x), z = fa(y), c = get(x);
if(!isrt(y)) son(z, get(y)) = x;
son(y, c) = son(x, c ^ 1), fa(son(x, c ^ 1)) = y;
son(x, c ^ 1) = y;
fa(y) = x, fa(x) = z;
pushup(y), pushup(x);
}
void splay(int x){
update(x);
for(int f = fa(x); f = fa(x), !isrt(x); rotate(x))
if(!isrt(f)) (get(f) == get(x) ? rotate(f) : rotate(x));
}
int access(int x){
int p;
for(p = 0; x; p = x, x = fa(x))
splay(x), rs(x) = p, pushup(x);
return p;
}
int findrt(int x){
int p = access(x);
while(pushdown(p), ls(p)) p = ls(p);
return splay(p), p;
}
void makert(int x){ access(x), splay(x), tag(x) ^= 1; }
int query(int x, int y){
makert(x);
if(findrt(y) != x) return -1;
int p = access(y);
return sum(p);
}
bool link(int x, int y){
makert(x);
if(findrt(y) == x) return 0;
fa(x) = y;
return 1;
}
void change(int x, int y){
splay(x); val(x) = y; pushup(x);
}
int n, a[N], m;
int main(){
cin.tie(nullptr)->sync_with_stdio(0);
cin >> n;
for(int i = 1; i <= n; ++i) cin >> val(i);
cin >> m;
for(int i = 1; i <= m; ++i){
string op;
int x, y;
cin >> op >> x >> y;
if(op[0] == 'b') cout << (link(x, y) ? "yes" : "no") << '\n';
else if(op[0] == 'e'){
int k = query(x, y);
if(k == -1) cout << "impossible";
else cout << k;
cout << '\n';
}
else change(x, y);
}
return 0;
}
P8364 IZBORI
求最大值是 trival 的。
考虑对于每个政党 \(i\),二分最终席位的最小值 \(k\)。分票的最后一定存在一个拿到 \(s_j\) 个席位的政党 \(j\),一定满足 \({V_j \over s_j} > {V_i \over {k + 1}}\),但是反过来,一个拿到 \(s_j\) 的席位的政党,这个不等式也可能是小于。可是这重要吗?如果满足了前面那个式子,那么这 \(s_j\) 个席位是一定不会被分给第 \(i\) 个政党的,这就足够了。或者我们这样理解,要使得第 \(j\) 个政党给答案贡献 \(s_j\) 个席位,需要的票数 \(V_j > s_j \times {V_i \over {k + 1}}\)。如果你记录一下最终 dp 出来的票数,然后按这个模拟,会发现一定存在这个能限制住 \(i\) 的政党,因为席位总是在除了 \(i\) 以外的政党之间重新分配。
还要注意一个问题,就是得保证 \(V_j \ge a_j\)。因此要 dp 增量,而不能 dp 总票数。
然后就是一个简单的背包了,由于小于 5% 的直接去除(注意特判这个),所以最多只需要 dp 基础票数最大的二十个。记得考虑编号大小带来的细节问题。
想了很久的一个小问题,既然 \(V_j\) 有 \(a_j\) 的下限限制,那么如果取更小的 \(a_j\) 不就能取到更小的 \(V_j\) 吗,那为啥只用 dp 最大的二十个呢?还是因为这个 5% 的限制。对于 >5% 的那些是一定会参选的,而对于前二十个还没到 5% 的那些,程序的确会从下限开始取,但也得保证他们到 5%。
Code
#include <bits/stdc++.h>
using namespace std;
#define int long long
const int N = 1e2 + 5, M = 2e2 + 5;
int f[N][M], n, m, a[N], idx, sumV, s[N], lstV, mx[N], id[N];
void chmin(int &x, int y){ x = min(x, y); }
void chmax(int &x, int y){ x = max(x, y); }
bool check(int k){
memset(f, 0x3f, sizeof(f));
f[0][0] = 0;
for(int it = 1; it <= min(20ll, n); ++it){
int i = id[it];
for(int j = 0; j <= m; ++j) f[it][j] = f[it - 1][j];
if(i == idx) continue;
for(int j = 0; j <= m; ++j){
for(int r = 0; r <= j; ++r){
int V = max(0ll, (sumV + 19) / 20 - a[i]);
if(i < idx) chmax(V, (a[idx] * r + k) / (k + 1) - a[i]);
if(i > idx) chmax(V, (a[idx] * r) / (k + 1) + 1 - a[i]);
if(r == 0) V = 0;
chmin(f[it][j], f[it - 1][j - r] + V);
}
}
}
return f[min(n, 20ll)][m - k] <= lstV;
}
signed main(){
cin.tie(nullptr)->sync_with_stdio(0);
cin >> sumV >> n >> m;
for(int i = 1; i <= n; ++i) cin >> a[i], lstV += a[i], id[i] = i;
lstV = sumV - lstV;
for(int i = 1; i <= n; ++i){
a[i] += lstV;
memset(s, 0, sizeof(s));
auto cmp = [](int x, int y){
int q = a[x] * (s[y] + 1), w = a[y] * (s[x] + 1);
return q == w ? x < y : q > w;
};
for(int j = 1; j <= m; ++j){
int tgt = -1;
for(int k = 1; k <= n; ++k){
if(a[k] * 20 >= sumV){
if(tgt == -1) tgt = k;
if(cmp(k, tgt)) tgt = k;
}
}
s[tgt]++;
}
cout << (mx[i] = s[i]) << ' ';
a[i] -= lstV;
}
cout << '\n';
sort(id + 1, id + 1 + n, [](int x, int y){
return a[x] == a[y] ? x < y : a[x] > a[y];
});
for(idx = 1; idx <= n; ++idx){
if(a[idx] * 20 < sumV) cout << 0;
else{
int l = 0, r = mx[idx];
while(l < r){
int mid = (l + r) >> 1;
if(check(mid)) r = mid;
else l = mid + 1;
}
cout << l;
}
cout << ' ';
}
return 0;
}
P6400 UMNOZAK
考虑枚举这个数位积 \(k\)。具体来说枚举位数 \(w\),然后考虑分给 \(1 \dots 9\)(枚举出现次数),由插板法知道方案数是 \({w + 9 - 1} \choose {9 - 1}\)。然后可以用 \(O(w)\) 的组合方法算出满足前面出现次数限制且 $ \le {B \over k} $ 的数有多少个,加到答案里就行(这一个就是类似数位 dp)。复杂度是 \(O(\sum_{w = 1}^{log(B)} w \times {{w + 9 - 1} \choose {9 - 1}})\)。
一些细节没想清楚调了贼久,同时喜提最劣解
Code
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
ll l, r;
ll pw[19], fac[19], sum, x[10], a[19], tmpx[10];
void dfs(int w, int lst, int nw, ll k, ll B, ll mn){
if(mn * k > B) return;
if(lst == 0){
ll b = B / k, tot = 0, cnt = 1;
while(b) a[++tot] = b % 10, b /= 10;
for(int i = 1; i <= 9; ++i) tmpx[i] = x[i], cnt *= fac[x[i]];
if(tot > w) sum += fac[w] / cnt;
else if(tot == w){
reverse(a + 1, a + 1 + tot);
for(int i = 1; i <= w; ++i){
for(int j = 1; j < (a[i] + (i == w)); ++j)
sum += tmpx[j] * fac[w - i] / cnt;
if(!tmpx[a[i]]) break;
else cnt /= fac[tmpx[a[i]]], tmpx[a[i]]--, cnt *= fac[tmpx[a[i]]];
}
}
return;
}
if(nw > 9) return;
ll mi = 1, sm = 0;
for(int i = 0; i <= lst; ++i){
x[nw] = i;
dfs(w, lst - i, nw + 1, k * mi, B, mn + sm);
if(i == lst) break;
sm += nw * pw[lst - i - 1];
mi *= nw;
}
x[nw] = 0;
}
ll query(ll B){
if(B == 0) return 0;
sum = 0;
for(int i = 0; i <= 18 && B >= pw[i]; ++i){
dfs(i + 1, i + 1, 1, 1, B, 0);
}
return sum;
}
int main(){
cin.tie(nullptr)->sync_with_stdio(0);
cin >> l >> r;
pw[0] = fac[0] = fac[1] = 1;
for(int i = 2; i <= 18; ++i) fac[i] = fac[i - 1] * i;
for(int i = 1; i <= 18; ++i) pw[i] = pw[i - 1] * 10;
cout << query(r) - query(l - 1) << '\n';
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号