BZOJ 杂题选记(8.31 - 9.6)
P3493 WSP-Island
调了很久,并发现了一些求半平面交的细节。
1.优雅地求两个直线的交点
考虑 \(l_1 : P_1 + k \times \vec{v_1}\) 和 \(l_2 : P_2 + t \times \vec{v_2}\) 的交点 \(O\)。假设 \(\vec{P_2O} = s \times \vec{v_2}\)。因为 \(O\) 也在 \(l_1\) 上,所以 \(\vec{P_1O} \times \vec{v_1} = 0\),那么 \((\vec{P_1P_2} + \vec{P_2O}) \times \vec{v_1} = 0\)。拆开,带入,整理一下得 \(s = -\frac{\vec{P_1P_2} \times \vec{v_1}}{\vec{v_2} \times \vec{v_1}}\)。这个就非常好看了,然后把 \(s\) 带回去就行。
2.无穷交的情况不添加边界是没办法处理的
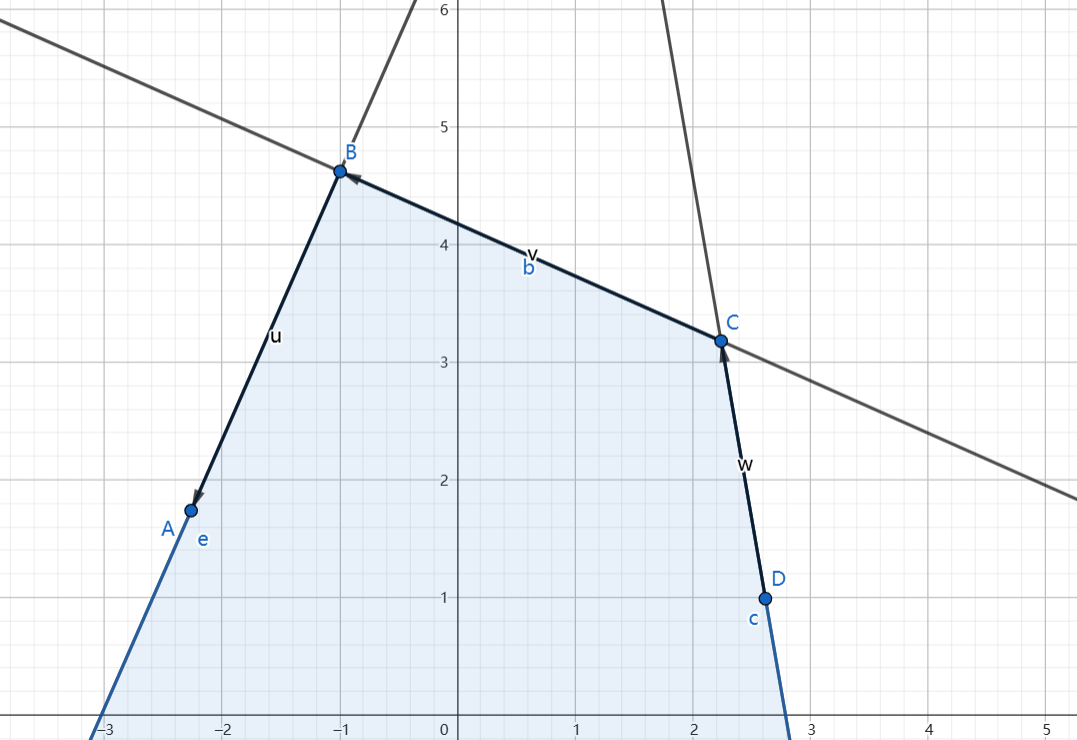
这个图就是一个反例,可以自己手模一下。那为什么按单调栈求上凸包的方法可以处理这种问题呢,这主要是由于斜率和极角的性质不同导致的。
Code
#include <bits/stdc++.h>
using namespace std;
typedef long double ldb;
const int N = 1e5 + 5;
const ldb eps = 1e-12, pi = acos(-1);
int n, m, tot;
struct vec{
ldb x, y;
vec operator + (vec b){ return {x + b.x, y + b.y}; }
vec operator - (vec b){ return {x - b.x, y - b.y}; }
vec operator * (ldb k){ return {k * x, k * y}; }
}p[N];
ldb len(vec x){ return sqrt(x.x * x.x + x.y * x.y); }
ldb cross(vec a, vec b){ return a.x * b.y - a.y * b.x; }
struct line{
vec P, v; ldb ang;
void assign(vec p1, vec p2){ P = p1, v = p2 - p1, ang = atan2(v.y, v.x);}
}li[N];
vec inter(line a, line b){
ldb t = -cross(b.P - a.P, a.v) / cross(b.v, a.v);
return b.P + b.v * t;
}
int q[N], l = 1, r = 1;
bool right(vec a, line b){ return cross(a - b.P, b.v) >= 0; }
void solve(){
sort(li + 1, li + 1 + tot, [](line a, line b){
return ((fabs(a.ang - b.ang) < eps) ? (cross(b.v, a.P - b.P) >= 0) : a.ang < b.ang);
});
q[1] = 1;
for(int i = 2; i <= tot; ++i){
if(fabs(li[i].ang - li[i - 1].ang) < eps) continue;
while(l < r && right(inter(li[q[r]], li[q[r - 1]]), li[i])) --r;
while(l < r && right(inter(li[q[l]], li[q[l + 1]]), li[i])) ++l;
q[++r] = i;
}
while(l < r && right(inter(li[q[r]], li[q[r - 1]]), li[q[l]])) r--;
q[++r] = q[l];
}
vector<int> e[N];
int main(){
cin.tie(nullptr)->sync_with_stdio(0);
cin >> n >> m;
for(int i = 1; i <= n; ++i){
cin >> p[i].x >> p[i].y;
}
for(int i = 1; i <= m; ++i){
int u, v;
cin >> u >> v;
if(u < v) swap(u, v);
e[u].push_back(v);
}
for(int i = 1; i <= n; ++i){
sort(e[i].begin(), e[i].end());
int mex = 1;
for(int j : e[i]){
if(mex == j) ++mex;
else break;
}
if(i == n && mex == 1) return cout << len(p[n] - p[1]) << '\n', 0;
if(mex < i) li[++tot].assign(p[i], p[mex]);
}
li[++tot].assign(p[1], p[n]);
solve();
ldb ans = 0;
vec lst = inter(li[q[l]], li[q[l + 1]]);
for(int i = l + 1; i <= r - 1; ++i){
vec tmp = inter(li[q[i]], li[q[i + 1]]);
ans += len(tmp - lst);
lst = tmp;
}
ans -= len(p[n] - p[1]) - len(lst - inter(li[q[l]], li[q[l + 1]]));
cout << fixed << setprecision(10) << ans;
return 0;
}
P3485 BAJ-The Walk of Bytie-boy
状态还是蛮好想的,主要是转移顺序怎么办。
trick : 考虑用 bfs 钦定转移顺序。然后发现直接转移是 \(O(M ^ 2)\) 的。考虑先枚举一边,定义一下辅助数组 \(g\),这道题就可以了。复杂度是 \(O(NM + N ^ 2)\)。
Code
#include <bits/stdc++.h>
using namespace std;
const int N = 4e2 + 5;
vector<int> e[N][26], _e[N][26];
int f[N][N], g[N][N][26], n, m, a[N];
string s;
struct node{
int x, y, c;
}fpre[N][N], gpre[N][N][26];
queue<node> Q, q;
void prt(int x, int y){
if(!x || !y || x == y) return;
int u = fpre[x][y].x, v = fpre[x][y].y, c = fpre[x][y].c;
s.push_back((char)c + 'a');
prt(gpre[u][v][c].x, gpre[u][v][c].y);
}
int main(){
cin.tie(nullptr)->sync_with_stdio(0);
cin >> n >> m;
for(int i = 1; i <= m; ++i){
int u, v; char c;
cin >> u >> v >> c;
int x = c - 'a';
e[u][x].push_back(v);
_e[v][x].push_back(u);
}
memset(f, 0x3f, sizeof(f));
memset(g, 0x3f, sizeof(g));
for(int i = 1; i <= n; ++i){
Q.push(node{i, i, -1});
f[i][i] = 0;
}
for(int i = 1; i <= n; ++i){
for(int j = 0; j < 26; ++j){
for(int v : e[i][j])
Q.push(node{i, v, -1}), f[i][v] = 1, fpre[i][v] = node{0, 0, j};
}
}
while(!Q.empty()){
while(!Q.empty()){
int i = Q.front().x, j = Q.front().y;
Q.pop();
for(int c = 0; c < 26; ++c){
for(int v : e[j][c]){
if(g[i][v][c] > f[i][j] + 1){
g[i][v][c] = f[i][j] + 1;
gpre[i][v][c] = node{i, j, -1};
q.push(node{i, v, c});
}
}
}
}
while(!q.empty()){
int i = q.front().x, j = q.front().y, c = q.front().c;
q.pop();
for(int u : _e[i][c]){
if(f[u][j] > g[i][j][c] + 1){
f[u][j] = g[i][j][c] + 1;
fpre[u][j] = node{i, j, c};
Q.push(node{u, j, -1});
}
}
}
}
int t;
cin >> t;
for(int i = 1; i <= t; ++i) cin >> a[i];
for(int i = 1; i < t; ++i){
int ans = f[a[i]][a[i + 1]];
if(ans == f[0][0]) cout << -1 << '\n';
else{
s.clear();
prt(a[i], a[i + 1]);
string tmp = s.substr(0, ans / 2);
reverse(tmp.begin(), tmp.end());
cout << ans << ' ' << s + tmp << '\n';
}
}
return 0;
}
P3494 KOD-The Code
洛谷的翻译就是依托,去 loj 看吧、
首先考虑题意的转化,01trie 肯定要建出来。我们发现解码的过程就是沿着 trie 走,走到叶子了(叶子一定是某个编码的结尾),就把这个编码对应的字符输出出来,然后跳回根 \(T\),继续走。
又发现,这个同步编码 \(\omega\) 所满足的性质是:从根开始走,走过任意字符编码的后缀,任意若干字符和 \(\omega\) 要回到根,这样 \(\omega\) 之后的解码才不会受影响。
然后就可以分三步走,第一步先求出任意字符编码的后缀可以到达树上的点的集合 \(V\)。这一步是 trival 的,直接建 AC 自动机然后跳 fail 就可以了。这里复杂度是 \(O(N)\) 的。
第二步就是要求出从 \(V\) 中的点开始走,走过若干任意字符,能到达的点 \(V'\)。最先想到的是暴力 bfs,复杂度是 \(O(NL)\) 的。然后就是比较神的一步: 在 trie 树上走代替暴力 bfs。具体来说,假设我们现在要从 \(u\) 这个点开始扩展。为方便叙述,定义一个 \(\operatorname{move}(u, S)\) 表示从 \(u\) 开始走过 \(S\) 这个 01 串会到达哪个树上的点。bfs 要求我们每次扩展 \(u\) 时遍历所有字符集中的 \(S_i\) 并找到 \(\operatorname{move}(u, S_i)\)。考虑在 trie 上做这一步,具体来说我们在两颗 trie 上深搜,第一颗以 \(u\) 为起点,第二颗以 trie 的根为起点。每次同步移动两颗树上的点 \(\operatorname{move}(x, 0)\),\(\operatorname{move}(y, 0)\),然后继续搜索,对于 1 儿子也是同理。边界是,如果此时 \(y\) 走到了一个叶子节点,那么就将此时的 \(x\) 加入 \(V'\),并返回。注意 \(x\) 走到叶子了就把它移到根继续搜就行(这是解码的过程告诉我们的)。这样子,每次扩展就是第二颗 trie 上走一遍,因此复杂度是 \(O(N^2)\) 的。接着简单剪枝,对于从起点 \(u\) 走到某个叶子的部分就暴力做,走到叶子之后,此时 \(x\) 会跳回根,记录一下此时的 \(y\)。我们发现对于相同的 \(y\),\(\operatorname{dfs}(T,y)\) 做一遍就行了,这样的话对于不同的 \(y\),\(y\) 子树内的点都会被遍历一次,复杂度就是 \(O(\sum_y siz_y)\)。在最后我们将说明这个复杂度是正确的。
第三步就是要求满足条件的 \(\omega\),即 $ \forall u \in V', \operatorname{move}(u, \omega) = T$。还是考虑在 trie 上做这个,跟第二步中的做法非常类似,只是边界操作有所不同。第一颗 trie 以 \(u\) 为起点,第二课还是以根为起点。如果此时 \(y\) 走到了叶子节点,但是 \(x\) 不在叶子节点,说明这个 \(\operatorname{move}(u, \omega)\) 走不到根,那么就标记这个 \(y\) 对应的编码为非同步编码。对每个 \(u\) 都做一遍就行,剪枝方法也一样,复杂度还是 \(O(\sum_y siz_y)\)。
最后考虑我们证明 \(\sum_y siz_y = 1 + 2 \times L\)。POI 官解是归纳证的,归纳法对我们加深理解并没有什么好处,我很菜也想不到别的办法,但还是为了完整性写在这里。证明首先需要一个观察,发现题目给的 trie 一定是严格二叉树,那么对于一颗叶子节点数量为 \(n\) 的严格二叉树,总结点数量是 \(2 \times n - 1\)。这是因为合并 \(n\) 个叶子节点需要 \(n - 1\) 次。假设 \(T\) 这颗 trie 中包含了 \(K\) 个 01 串,每个串是 \(s_i\)。对于一颗只有根的 trie,\(1 = 1 + 2 \times 0\) 满足。考虑两颗 trie \(T_1\),\(T_2\) 合并在 \(T\) 上时。假设 \(T_1\) 和 \(T_2\) 满足归纳假设,有如下推导。
\(\begin{aligned}
\sum_{y \in T} siz_y &= \sum_{u \in T_1} siz_u + \sum_{v \in T_2} siz_v + siz_{T_1} + siz_{T_2} + 1 \\
&= (1 + 2\sum_{i = 1}^{K_1} |s_i|) + (1 + 2\sum_{i = 1}^{K_2} |s_i|) + 2|K_1| - 1 + 2|K_2| - 1 + 1 \\
&= 1 + 2(\sum_{i = 1}^{K_1} |s_i| + \sum_{i = 1}^{K_2} |s_i| + |K_1| + |K_2|) \\
&= 1 + 2(\sum_{i = 1}^{K_1} (|s_i| + 1) + \sum_{i = 1}^{K_2} (|s_i| + 1)) \\
&= 1 + 2 \times \sum_{i = 1}^{K} |s_i|
\end{aligned}\)
这就说明总的复杂度是 \(O(N + L)\) 的,可以通过。
Code
#include <bits/stdc++.h>
using namespace std;
const int N = 1.5e6 + 5;
int ed[N], tr[N][2], fail[N], fa[N];
bitset<N> vis, ans;
char c;
int tot, n;
bool isleaf(int u){ return ed[u] <= n && ed[u] != 0; }
queue<int> q;
void init(){
for(int i = 0; i < 2; ++i) if(tr[0][i]) q.push(tr[0][i]);
while(!q.empty()){
int u = q.front();
q.pop();
for(int i = 0; i < 2; ++i){
if(tr[u][i]) fail[tr[u][i]] = tr[fail[u]][i], q.push(tr[u][i]);
else tr[u][i] = tr[fail[u]][i];
}
}
for(int i = 0; i <= tot; ++i){
if(isleaf(i)) tr[i][0] = tr[i][1] = 1;
}
for(int i = 1; i <= tot; ++i){
if(!ed[i]) continue;
int p = i;
while(p != 0){
if(!ed[p]) ed[p] = n + 1;
p = fail[p];
}
}
}
void get(int x, int y){
if(isleaf(x)){
if(vis[y]) return;
vis[y] = 1;
get(0, y);
}
else{
if(isleaf(y)){
if(!ed[x]) ed[x] = n + 1, q.push(x);
return;
}
get(tr[x][0], tr[y][0]);
get(tr[x][1], tr[y][1]);
}
}
void solve(){
for(int i = 0; i <= tot; ++i){
if(ed[i] && !isleaf(i)) q.push(i);
}
while(!q.empty()){
get(q.front(), 0);
q.pop();
}
}
void getans(int x, int y){
if(isleaf(y)){
if(!isleaf(x)) ans[y] = 0;
return;
}
if(isleaf(x)){
if(vis[y]) return;
vis[y] = 1;
getans(0, y);
}
else{
getans(tr[x][0], tr[y][0]);
getans(tr[x][1], tr[y][1]);
}
}
int main(){
cin.tie(nullptr)->sync_with_stdio(0);
cin >> n;
int p = 0, cnt = 0;
for(int i = 1; i <= n; ++i){
cin >> c;
if(c == 'X') ed[p] = ++cnt, ans[p] = 1;
else if(c == 'B') p = fa[p];
else{
int x = c - '0';
++tot;
tr[p][x] = tot;
fa[tot] = p;
p = tot;
}
}
init(), solve();
vis.reset();
for(int i = 0; i <= tot; ++i){
if(ed[i] && !isleaf(i)) getans(i, 0);
}
cout << ans.count() << '\n';
for(int i = 0; i <= tot; ++i){
if(ans[i]) cout << ed[i] << '\n';
}
return 0;
}
P3491 SLW-Words
很神的思维题,完全不会。
有一些性质:因为 \(h(k) = h(h(k - 1))\),所以 \(h(h(k_1 - 1)h(k_2 - 1)...h(k_n - 1)) = h(k_1)h(k_2)...h(k_n)\)。如果 \(h(k_1)h(k_2)...h(k_n)\) 是某个 \(h(m)\) 的子串。这意味着,\(h(h(k_1 - 1)h(k_2 - 1)...h(k_n - 1))\) 是 \(h(h(m-1))\) 的子串。由于 \(h\) 是单射,感性理解一下,这意味着 \(h(k_1 - 1)h(k_2 - 1)...h(k_n - 1)\) 是 \(h(m - 1)\) 的子串。反过来说,如果有 \(h(k_1 - 1)h(k_2 - 1)...h(k_n - 1)\) 是 \(h(m - 1)\) 的子串,那 \(h(k_1)h(k_2)...h(k_n)\) 也是 \(h(m)\) 的子串。然后我们就一直对 \(k\) 序列减一,当发现一些数变成 0 时,做一些特殊的判断。具体来说,可以发现 \(h(m)\) 一定不会出现连续的两个 \(0\) 和 \(101010\),而 \(h(5)0 = 101101010\),因此如果发现一个 \(k_i = 0\) 前面不是 \(k_{i-1} = 1\) 或者 \(3\),就 NIE。记得如果发现 \(k_1\) 变成 0 了,把它变成 2。因为在开头和末尾添加 1 或者删去 1 显然没有影响。如果最后只剩一个数了,那么原序列肯定就 TAK 了。
但我们发现这样做会有一些问题,比如 \(k_n = 3\) 时,\(101\) 不一定只由 \(10\) 变过来,也有可能是原序列中的 \(11\) 变成 \(1010\) 然后去掉 \(0\) 变过来的,\(k_n = 1\) 也类似。而且这种情况只有在 \(k_n\) 上才会发生。怎么修呢?我们可以考虑直接把 \(101\) 变成 \(10\) 再去进行减一的操作,这样就没问题了。而对于偶数和 \(k_n \ge 5\) 的奇数这种情况不会出现,理由和判断那里一样。
Code
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 1e5 + 5;
int k[N], n;
bool solve(){
cin >> n;
for(int i = 1; i <= n; ++i) cin >> k[i];
while(n > 1){
if(k[1] == 0) k[1] = 2;
if(k[n] == 1) k[n] = -1;
if(k[n] == 3) k[n] = 2;
for(int i = 2; i <= n; ++i){
if(k[i] == 0){
if(k[i - 1] == 1) k[i - 1] = 2, k[i] = -1;
else if(k[i - 1] == 3) k[i - 1] = 2, k[i] = 2;
else return 0;
}
}
int m = 0;
for(int i = 1; i <= n; ++i) if(k[i] != -1)
k[++m] = k[i];
n = m;
for(int i = 1; i <= n; ++i) k[i]--;
}
return 1;
}
int main(){
cin.tie(0)->sync_with_stdio(0);
int T; cin >> T;
while(T--) cout << (solve() ? "TAK" : "NIE") << '\n';
return 0;
}
P4298 祭祀
Dilworth 定理。主要内容是最小链覆盖 = 最大反链个数,注意在 Hasse 图上,最小链覆盖是可重的,传递闭包后可以变为不可重。
一个经典模型:就是如何求 DAG 上的最小链覆盖。建模方法看题解吧。
方案就按题解说的求,记录一下最大独立集的一种求法。
从网络流的角度看,最小点覆盖问题就是最小割问题:选择左部点,相当于切割它与源点的连边;选择右部点,相当于切割它与汇点的连边。
把最小点覆盖的集合 \(S\) 求出来,那么最大独立集就是 \(V - S\)。因为如果有两个最大独立集里的点 \(u\),\(v\) 连通, 那么 \((u,v)\) 这条边就没被覆盖。
Code
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 2e2 + 5;
#define in(i) i
#define out(i) i + n
int s, t, dep[N], head[N], tot = 1, cur[N], n, m;
bitset<N> g[N], on, vis;
struct edge{
int v, pre, f;
}e[N * N];
void init(){
memset(head, 0, sizeof(head));
tot = 1;
}
void adde(int u, int v){
e[++tot] = {v, head[u], 1}, head[u] = tot;
e[++tot] = {u, head[v], 0}, head[v] = tot;
}
bool bfs(){
memset(dep, 0, sizeof(dep));
memcpy(cur, head, sizeof(cur));
dep[s] = 1;
queue<int> q; q.push(s);
while(!q.empty()){
int u = q.front(); q.pop();
for(int k = head[u]; k; k = e[k].pre){
int v = e[k].v, f = e[k].f;
if(f){
if(dep[v]) continue;
dep[v] = dep[u] + 1;
q.push(v);
}
}
}
return dep[t];
}
int dinic(int u, int ff){
if(u == t) return ff;
int su = 0;
for(int k = cur[u]; k; k = e[k].pre){
int v = e[k].v, &f = e[k].f;
if(dep[v] != dep[u] + 1) continue;
if(f){
cur[u] = k;
int sv = dinic(v, min(ff - su, f));
f -= sv, e[k ^ 1].f += sv;
su += sv;
if(su == ff) return su;
}
}
if(su == 0) dep[u] = 0;
return su;
}
void dfs(int u){
if(vis[u]) return;
vis[u] = on[u] = 1;
for(int k = head[u]; k; k = e[k].pre){
int v = e[k].v;
if(e[k].f) dfs(v);
}
}
int maxflow(){
int ret = 0;
while(bfs()) ret += dinic(s, 1e9);
return ret;
}
int main(){
cin.tie(0)->sync_with_stdio(0);
cin >> n >> m;
for(int i = 1; i <= m; ++i){
int u, v;
cin >> u >> v;
g[u][v] = 1;
}
for(int k = 1; k <= n; ++k){
for(int i = 1; i <= n; ++i){
if(g[i][k]) g[i] |= g[k];
}
}
s = 2 * n + 1, t = 2 * n + 2;
for(int i = 1; i <= n; ++i) adde(s, out(i)), adde(in(i), t);
for(int i = 1; i <= n; ++i){
for(int j = 1; j <= n; ++j){
if(g[i][j]) adde(out(i), in(j));
}
}
int ans = n - maxflow();
cout << ans << '\n';
dfs(s);
for(int i = 1; i <= n; ++i) on[i].flip();
for(int i = 1; i <= n; ++i) cout << (on[in(i)] && on[out(i)]);
cout << '\n';
for(int x = 1; x <= n; ++x){
init();
int cnt = 0;
for(int i = 1; i <= n; ++i) vis[i] = (x == i || g[x][i] || g[i][x]);
for(int i = 1; i <= n; ++i) if(!vis[i]) adde(s, out(i)), adde(in(i), t), ++cnt;
for(int i = 1; i <= n; ++i){
for(int j = 1; j <= n; ++j){
if(vis[i] || vis[j]) continue;
if(g[i][j]) adde(out(i), in(j));
}
}
int res = cnt - maxflow();
cout << (res == ans - 1);
}
return 0;
}
P4527 奥运抽奖
怎么求出 \(L\) 集合呢?trick:考虑一种指针的做法,比方说对于 \({2, 3, 5, 6}\),假设我们已经求出了 \(L\) 的一部分 \(A\)。扩展第 \(i\) 个时,把 \(p_2\) 后移到第一个 \(A_{p_2} \times 2 > A_{i-1}\) 的地方,对于其他也是同理,然后找出其中的最小的(比大小取对数就行),加入进去。
然后再考虑一下 \(f(S) = d +(1 + qd) \times f(S / d)\) 有什么性质。呃呃呃可以类似数列待定系数法推一下通项,可以算出 \(f(S) + \frac{1}{q} = (1 + qd)(f(S / d) + \frac{1}{q})\),去一下分母,得到 \(qf(S) + 1 = (1 + qd)(qf(S / d) + 1)\),也就是 \(qf(S) + 1 = \Pi_{k \in S} (1 + qk)\)。进一步发现对于 \(B \subset A,C = A - B,qf(A) + 1 = (qf(B) + 1)(qf(C) + 1) \implies f(A) = f(B) + f(C) + q \times f(B) \times f(C)\),这个性质非常重要,这意味着合并两个集合变成非常容易的事情。
接着考虑询问 \(a,b\),实际上我们发现只要以 \({2,3,5}\) 为底,\(T_{a,b} = \{x | x \in L, \nu_2(a) \le \nu_2(x) \le \nu_2(b) \land \nu_3(a) \le \nu_3(x) \le \nu_3(b) \land \nu_5(a) \le \nu_5(x) \le \nu_5(b) \}\)。然后三维线段树维护这个就行。
一个细节,如果全都以 \({2, 3, 5}\) 为底,会在题目给定底 \(\{6\}\) 和 \(\{5,6\}\) 时炸掉。比方说 \(\{5, 6\}\) 达到了 \(422 \times 422 \times 470 = 83,699,480\),再加上线段树自带常数,试了一下不能通过。至于怎么算出来过不了的我先鸽着
Code
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef array<int, 5> arr;
typedef long double ldb;
const int N = 1e5 + 5;
ll q, mod, pw[6][N];
struct Segment{
int tot = 0, siz[4][2];
#define ls(p) tr[p].ls
#define rs(p) tr[p].rs
#define rt(p) tr[p].rt
struct node{
int ls, rs, rt;
ll val;
}tr[N * 16];
ll merge(ll a, ll b){ return (a + b + q * a % mod * b % mod) % mod; }
void pushup(int p){ tr[p].val = merge(tr[ls(p)].val, tr[rs(p)].val); }
void add(int z, ll k, int &p, int pl, int pr){
if(!p) p = ++tot;
if(pl == pr){ return tr[p].val = merge(tr[p].val, k), void(); }
int mid = (pl + pr) >> 1;
if(z <= mid) add(z, k, ls(p), pl, mid);
else add(z, k, rs(p), mid + 1, pr);
pushup(p);
}
void upd(int y, int z, ll k, int &p, int pl, int pr){
if(!p) p = ++tot;
add(z, k, rt(p), siz[3][0], siz[3][1]);
if(pl == pr) return;
int mid = (pl + pr) >> 1;
if(y <= mid) upd(y, z, k, ls(p), pl, mid);
else upd(y, z, k, rs(p), mid + 1, pr);
}
void update(int x, int y, int z, ll k, int &p, int pl, int pr){
if(!p) p = ++tot;
upd(y, z, k, rt(p), siz[2][0], siz[2][1]);
if(pl == pr) return;
int mid = (pl + pr) >> 1;
if(x <= mid) update(x, y, z, k, ls(p), pl, mid);
else update(x, y, z, k, rs(p), mid + 1, pr);
}
ll qry(int p, int pl, int pr, int L, int R){
if(!p) return 0;
if(L <= pl && R >= pr) return tr[p].val;
int mid = (pl + pr) >> 1;
ll ret = 0;
if(L <= mid) ret = qry(ls(p), pl, mid, L, R);
if(R > mid) ret = merge(ret, qry(rs(p), mid + 1, pr, L, R));
return ret;
}
ll ask(int p, int pl, int pr, int Ly, int Ry, int Lz, int Rz){
if(!p) return 0;
if(Ly <= pl && Ry >= pr) return qry(rt(p), siz[3][0], siz[3][1], Lz, Rz);
int mid = (pl + pr) >> 1;
ll ret = 0;
if(Ly <= mid) ret = ask(ls(p), pl, mid, Ly, Ry, Lz, Rz);
if(Ry > mid) ret = merge(ret, ask(rs(p), mid + 1, pr, Ly, Ry, Lz, Rz));
return ret;
}
ll query(int p, int pl, int pr, int Lx, int Rx, int Ly, int Ry, int Lz, int Rz){
if(!p) return 0;
if(Lx <= pl && Rx >= pr) return ask(rt(p), siz[2][0], siz[2][1], Ly, Ry, Lz, Rz);
int mid = (pl + pr) >> 1;
ll ret = 0;
if(Lx <= mid) ret = query(ls(p), pl, mid, Lx, Rx, Ly, Ry, Lz, Rz);
if(Rx > mid) ret = merge(ret, query(rs(p), mid + 1, pr, Lx, Rx, Ly, Ry, Lz, Rz));
return ret;
}
}T;
int bse[4], tot, cnt, v[10], buc[7][4], tp[7], s[N], Rt;
ldb Log[10];
arr a[N];
bool ge(arr x, arr y){
ldb ret = 0;
for(int i = 1; i <= tot; ++i){
ret += (x[i] - y[i]) * Log[bse[i]];
}
return ret >= 0;
}
bool fl[7];
int main(){
cin.tie(nullptr)->sync_with_stdio(0);
for(int i = 2; i <= 6; ++i) {
cin >> fl[i];
Log[i] = log(i);
if(fl[i]){
v[++cnt] = i;
}
}
if(cnt == 1 && fl[6]){
tot = 1, bse[1] = 6;
}
else if(cnt == 2 && fl[5] && fl[6]){
tot = 2, bse[1] = 5, bse[2] = 6;
}
else{
if(fl[2] || fl[4] || fl[6]) bse[++tot] = 2;
if(fl[3] || fl[6]) bse[++tot] = 3;
if(fl[5]) bse[++tot] = 5;
}
for(int i = 1; i <= cnt; ++i){
for(int j = 1; j <= tot; ++j){
while(v[i] % bse[j] == 0)
buc[i][j]++, v[i] /= bse[j];
}
}
for(int j = 1; j <= 3; ++j) pw[j][0] = 1;
cin >> mod >> q;
for(int i = 1; i <= 100000; ++i){
arr mn = arr{100000, 100000, 100000}, now;
for(int j = 1; j <= tot; ++j) (pw[j][i] = pw[j][i - 1] * bse[j]) %= mod;
auto move = [&](int i){
for(int j = 1; j <= tot; ++j) now[j] += buc[i][j];
};
for(int j = 1; j <= cnt; ++j){
now = a[tp[j]];
move(j);
while(ge(a[i - 1], now)){
tp[j]++;
now = a[tp[j]];
move(j);
}
mn = (ge(mn, now) ? now : mn);
}
a[i] = mn;
for(int j = 1; j <= tot; ++j){
if(T.siz[j][1] < a[i][j]) T.siz[j][1] = a[i][j];
}
}
for(int i = 1; i <= 100000; ++i) {
ll k = pw[1][a[i][1]] * pw[2][a[i][2]] % mod * pw[3][a[i][3]] % mod;
T.update(a[i][1], a[i][2], a[i][3], k, Rt, T.siz[1][0], T.siz[1][1]);
}
int Q; cin >> Q;
while(Q--){
int x, y;
cin >> x >> y;
int Lx = a[x][1], Rx = a[y][1], Ly = a[x][2], Ry = a[y][2], Lz = a[x][3], Rz = a[y][3], l = T.siz[1][0], r = T.siz[1][1];
if(Lx > Rx || Ly > Ry || Lz > Rz) cout << 0 << '\n';
else cout << T.query(Rt, l, r, Lx, Rx, Ly, Ry, Lz, Rz) << '\n';
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号