BOLG-1

前言

难度

前两次都分别可以在一个晚上写完，第三次足足花费了我一周。
前两次的测试点清晰简单，第三次的测试点多而不易于发现。
第三次对输入格式的判断也是错综复杂。

题量

第一次的题目虽然有9道，但是每题的代码行数很少，第二次题目的量少且行数少，第三次看似只有三题，但是代码量远超前两次。

知识点

1-7-3首次使用split函数
```
public String[] split(String regex)
```
以regex分割，将字符串分割为字符串数组
1-7-6使用到equals函数
```
public boolean equals(Object o)
```
返回一个boolean类型，第一次了解到Java中字符串的比较不能直接使用‘==’。
1-7-8使用到ToCharArray函数和contains函数
```
public char[] toCharArray()
public boolean contains(CharSequence chars)
```
第一个函数字符串转化为字符数组，第二个函数判断字符串中是否包含某一个字符
2-7-2使用到index of函数和charAT函数
```
int indexOf(String str, int fromIndex)
char charAt(int index)
```
第一个函数从fromIndex位置开始向后遍历，返回第一次找到 str 字符串的位置第二个函数返回在index位置上的字符
3-7-1计算两点的距离
```
∣AB∣=√[(x1－x2)²+(y1－y2)²]
```
3-7-2直线的基本公式
```
Ax+By+C=0 
```
这里不采用 y=kx+b，避免后面判断直线平行等问题斜率不存在难以讨论。
3-7-3三角形面积的计算
```
采用S=|(x1y2-x1y3+x2y3-x2y1+x3y1-x2y2)|
而不用S=√p (p-a) (p-b) (p-c)
```
第二个海伦公式边长的时候已经开过根号，再次开根号会有误差过大的原因，所有我这边采用的是点求三角形面积

设计与分析

2-7-2串口字符解析

RS232是串口常用的通信协议，在异步通信模式下，串口可以一次发送5~8位数据，收发双方之间没有数据发送时线路维持高电平，相当于接收方持续收到数据“1”（称为空闲位），
发送方有数据发送时，会在有效数据（5~8位，具体位数由通信双方提前设置）前加上1位起始位“0”，在有效数据之后加上1位可选的奇偶校验位和1位结束位“1”。请编写程序，
模拟串口接收处理程序，注：假定有效数据是8位，奇偶校验位采用奇校验。

源码

import java.util.Scanner;
public class Main{
    public static void main(String[] args){
        Scanner sc = new Scanner( System.in );
        String str = sc.nextLine();
        if( str.length() < 11 || !str.contains("0")) {
            System.out.println("null data");
            return ;
        }else {
            int num = 0 ;
            int count = 1;
            while( str.length()-num >= 11) {
                num = str.indexOf("0",num);
                System.out.print(count+":");
                count++;
                if( str.charAt(num+10) != '1') {
                    System.out.print("validate error");
                }else {
                    int sum = 0;
                    for( int i=num ; i<num+10; i++) {
                        if( str.charAt(i) == '1') {
                            sum++;
                        }
                    }
                    if( sum % 2 != 1) {
                        System.out.print("parity check error");
                    }else {
                        System.out.print(str.substring(num+1, num+9));
                    }
                }
                System.out.println();
                num += 11 ;
            }
        }
            
    }
}

源码分析

奇校验判断代码
for( int i=num ; i<num+10; i++) {
                        if( str.charAt(i) == '1') {
                            sum++;
                        }
                    }
                    if( sum % 2 != 1) {
                        System.out.print("parity check error");
                    }else {
                        System.out.print(str.substring(num+1, num+9));
                    }

奇校验: 连同校验位使得所有位上的1相加为奇数
偶校验：连同校验位使得所有位上的1相加为偶数

3-7-1点线形系列1-计算两点之间的距离

4个double类型的实数，两个点的x，y坐标，依次是x1、y1、x2、y2，两个点的坐标之间以空格分隔，每个点的x,y坐标以英文“,”分隔。例如：0,0 1,1或0.1,-0.3 +3.5,15.6。
若输入格式非法，输出"Wrong Format"。
若输入格式合法但坐标点的数量超过两个，输出“wrong number of points”。

源码

import java.util.Scanner;

public class Main {

     /*用于判断输入是否合法
     * 合法就返回一个数组
     * 不合法就返回空
     */
    static String[] isLegal( String string) {
        String[] str = string.split(",| ");
        for( int i = 0 ; i < str.length; i++) {
            if(!str[i].matches("[+-]?[1-9]\\d*(\\.\\d+)?|[+-]?[0](\\.\\d+)?")) {
                System.out.println("Wrong Format");
                return null;
            }
        }
        
        if(str.length > 4) {
            System.out.println("wrong number of points");
            return null;
        }
        
        return str;
    }
    
    public static void main(String[] args) {
        Point p1 = new Point();
        Point p2 = new Point();
        Scanner sc = new Scanner(System.in);        
        String s = sc.nextLine();
        if( isLegal(s) != null) {
            String[] str = isLegal(s);
            p1.setPoint(str[0], str[1]);
            p2.setPoint(str[2], str[3]);
            System.out.println(p1.calculateDistance(p2));
        }
        

    }

}

class Point {

    private double x;
    private double y;
    
    /*public Point(double x, double y) {   //构造函数
        super();
        this.x = x;
        this.y = y;
    }
    
    double getx() {
        return this.x;
    }
    
    double gety() {
        return this.y;
    }*/
    
    
    /*用于判断输入是否合法
     * 合法就返回一个数组
     * 不合法就返回空
     */
    

    void setPoint( String stringx, String stringy) {    //建立点的 x y 坐标
        this.x = Double.parseDouble(stringx) ;
        this.y = Double.parseDouble(stringy) ;
    }

    double calculateDistance( Point point) {  //计算两点的距离
        double num = (this.x - point.x)*(this.x - point.x) + (this.y - point.y)*(this.y - point.y);
        return Math.sqrt(num);
    }
    
    boolean isCoincide( Point point) {    //判断两点是否重合
        return this.x==point.x&&this.y==point.y;
    }

}

源码分析

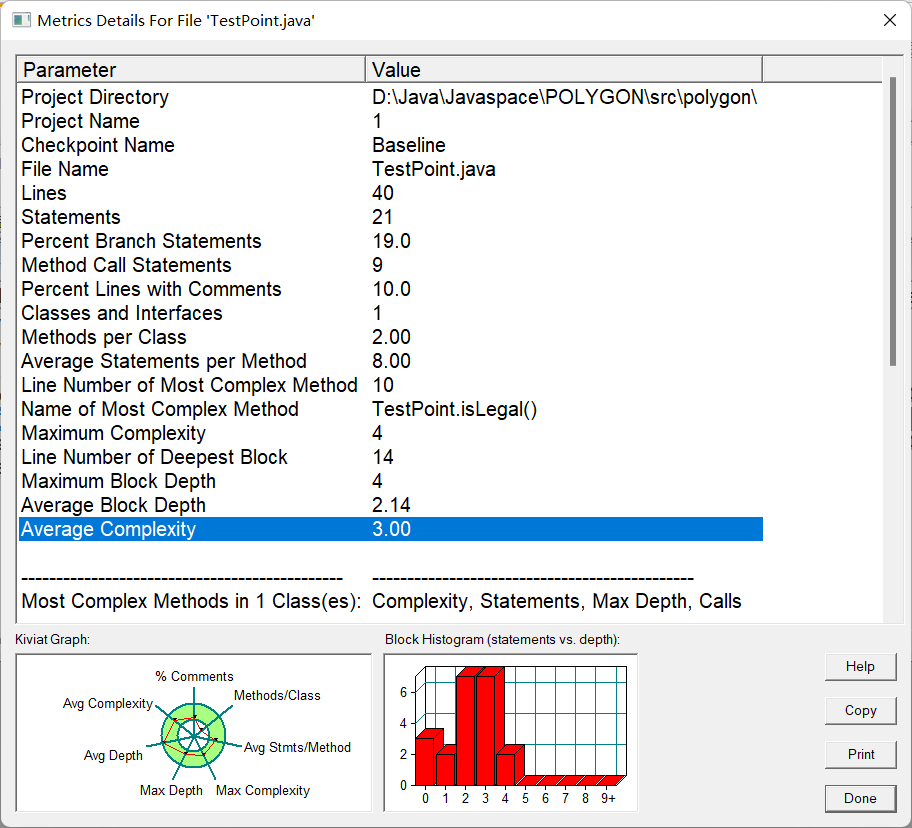
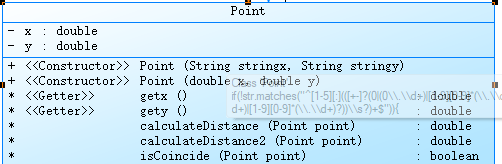
本题比较简单，平均圈复杂只有3，该题也仅仅用到一个类。

7-2 点线形系列2-线的计算

用户输入一组选项和数据，进行与直线有关的计算。选项包括：
1：输入两点坐标，计算斜率，若线条垂直于X轴，输出"Slope does not exist"。
2：输入三个点坐标，输出第一个点与另外两点连线的垂直距离。
3：输入三个点坐标，判断三个点是否在一条线上，输出true或者false。
4：输入四个点坐标，判断前两个点所构成的直线与后两点构成的直线是否平行，输出true或者false.
5：输入四个点坐标，计算输出前两个点所构成的直线与后两点构成的直线的交点坐标，x、y坐标之间以英文分隔","，并输出交叉点是否在两条线段之内（不含四个端点）的判断结果(true/false)，判断结果与坐标之间以一个英文空格分隔。若两条线平行，没有交叉点，则输出"is parallel lines,have no intersection point"。

源码

import java.util.Scanner;
public class Main {

/*用于判断输入是否合法
* 合法就返回一个数组
* 不合法就返回空
*/
static String[] isLegal( String string) {
String[] str = string.split(",| |:");

if( !string.contains(":") || !string.contains(",") || !string.contains(" ")) {
System.out.println("Wrong Format");
return null;
}
if(string.charAt(string.length()-1) ==' ' || string.charAt(string.length()-1) ==':' || string.charAt(string.length()-1) ==','|| !str[0].matches("[12345]") ) {
System.out.println("Wrong Format");
return null;
}
for( int i = 1 ; i < str.length; i++) {
if(!str[i].matches("[+-]?[1-9]\\d*(\\.\\d+)?|[+-]?[0](\\.\\d+)?")) {
System.out.println("Wrong Format");
return null;
}
}
int len = Integer.parseInt(str[0]) ;
if(len == 1) {
if(string.split(" ").length + string.split(":").length - string.split(",").length == 1 ) {
if( str.length != 5) {
System.out.println("wrong number of points");
return null;
}
}else {
System.out.println("Wrong Format");
return null;
}

}else if( len == 2 || len == 3) {
if(string.split(" ").length + string.split(":").length - string.split(",").length == 1) {
if( str.length != 7) {
System.out.println("wrong number of points");
return null;
}
}else {
System.out.println("Wrong Format");
return null;
}
}else if( len == 4 || len == 5) {
if(string.split(" ").length + string.split(":").length - string.split(",").length == 1) {
if( str.length != 9) {
System.out.println("wrong number of points");
return null;
}
}else {
System.out.println("Wrong Format");
return null;
}
}
return str;
}

public static void main(String[] args) {

Scanner sc = new Scanner(System.in);
String s = sc.nextLine();
if( isLegal(s) != null) {
String[] str = isLegal(s) ;
int len = Integer.parseInt(str[0]) ;
if(len == 1) {
Point p1 = new Point(str[1], str[2]);
Point p2 = new Point(str[3], str[4]);
if(p1.isCoincide(p2)) {
System.out.println("points coincide");
}else if(p1.getx() == p2.getx()) {
System.out.println("Slope does not exist");
}else {
Line l1 = new Line(p1,p2);
System.out.println(l1.getK());
}

}else if(len == 2) {
Point p1 = new Point(str[1], str[2]);
Point p2 = new Point(str[3], str[4]);
Point p3 = new Point(str[5], str[6]);
if(p2.isCoincide(p3)) {
System.out.println("points coincide");
}else {
Line l1 = new Line(p2,p3);
System.out.println(l1.calculateDistance(p1));
}
}else if(len == 3) {
Point p1 = new Point(str[1], str[2]);
Point p2 = new Point(str[3], str[4]);
Point p3 = new Point(str[5], str[6]);
if(p1.isCoincide(p2) ) {
System.out.println("points coincide");
}else {
Line l1 = new Line(p1,p2);
System.out.println(l1.judgePointOnLine(p3));
}
}else if(len == 4) {
Point p1 = new Point(str[1], str[2]);
Point p2 = new Point(str[3], str[4]);
Point p3 = new Point(str[5], str[6]);
Point p4 = new Point(str[7], str[8]);
if(p1.isCoincide(p2) || p3.isCoincide(p4)) {
System.out.println("points coincide");
}else {
Line l1 = new Line(p1,p2);
Line l2 = new Line(p3,p4);
System.out.println(l1.judgeParallel(l2));
}
}else if(len == 5) {
Point p1 = new Point(str[1], str[2]);
Point p2 = new Point(str[3], str[4]);
Point p3 = new Point(str[5], str[6]);
Point p4 = new Point(str[7], str[8]);
if(p1.isCoincide(p2) || p3.isCoincide(p4)) {
System.out.println("points coincide");
}else {
Line l1 = new Line(p1,p2);
Line l2 = new Line(p3,p4);
if(l1.judgeParallel(l2)) {
System.out.println("is parallel lines,have no intersection point");
}else {
Point p = l1.calculateIntersection(l2);
System.out.println(p.getx()+","+p.gety()+" "+ (l1.judgePointInLine(p)||l2.judgePointInLine(p)) );
}

}
}

}
}

}

class Line {

private Point point1;
private Point point2;
// 构造函数
public Line(Point point1, Point point2) {
super();
this.point1 = point1;
this.point2 = point2;
}
// 得到点一
Point getPoint1() {
return this.point1;
}
// 得到点二
Point getPoint2() {
return this.point2;
}
// 得到x的系数A
double getA() {
return point1.gety()-point2.gety();
}
// 得到y的系数B
double getB() {
return point2.getx()-point1.getx();
}
// 得到常数C
double getC() {
return point1.getx() * point2.gety() - point2.getx() * point1.gety();
}
// 得到直线的斜率
double getK() {
return (point1.gety()-point2.gety())/(point1.getx()-point2.getx());
}
// 计算点到直线的距离
double calculateDistance( Point point) {
double a = Math.abs( this.getA()*point.getx() + this.getB()*point.gety() + this.getC());
double b = Math.sqrt(this.getA() * this.getA() + this.getB()*this.getB());
return a/b;
}
// 判断点是否在直线上
boolean judgePointOnLine( Point point ){
return this.getA()*point.getx()+this.getB()*point.gety()+this.getC() == 0;
}
// 判断两直线是否平行
boolean judgeParallel( Line line ) {
if(this.getB() != 0 && line.getB() !=0)
return this.getK() == line.getK() ;
else if(this.getB() == 0 && line.getB() ==0){
return true;
}else {
return false;
}
}

// 计算线与线的交点
Point calculateIntersection( Line line) {
double x = (line.getC()*this.getB()-this.getC()*line.getB())/(this.getA()*line.getB()-line.getA()*this.getB());
double y = (line.getC()*this.getA()-this.getC()*line.getA())/(line.getA()*this.getB()-this.getA()*line.getB());
if(x!=0 && y!=0 ) {
Point point = new Point(x,y);return point;
}
else if(x==0 && y==0 ) {
Point point = new Point(0,0);return point;
}
else if(x==0 && y!=0 ) {
Point point = new Point(0,y);return point;
}
else {
Point point = new Point(x,0);return point;
}
}
// 判断交点是否在线段的内部
boolean judgePointInLine( Point point ) {
if( point.getx() < Math.max( this.point1.getx(), this.point2.getx() ) && point.getx() > Math.min( this.point1.getx() , this.point2.getx() ) || point.gety() < Math.max( this.point1.gety(), this.point2.gety() ) && point.gety() > Math.min( this.point1.gety() , this.point2.gety() ))
return true;
else
return false;
}

}

class Point {

private double x;
private double y;
// 构造函数
public Point(String stringx, String stringy) {
this.x = Double.parseDouble(stringx) ;
this.y = Double.parseDouble(stringy) ;
}
// 构造函数
public Point(double x, double y) {
super();
this.x = x;
this.y = y;
}
//得到点的x坐标
double getx() {
return this.x;
}
//得到点的y坐标
double gety() {
return this.y;
}
//计算两点的距离
double calculateDistance( Point point) {
double num = (this.x - point.x)*(this.x - point.x) + (this.y - point.y)*(this.y - point.y);
return Math.sqrt(num);
}
//判断两点是否重合
boolean isCoincide( Point point) {
return this.x==point.x&&this.y==point.y;
}

}

源码分析

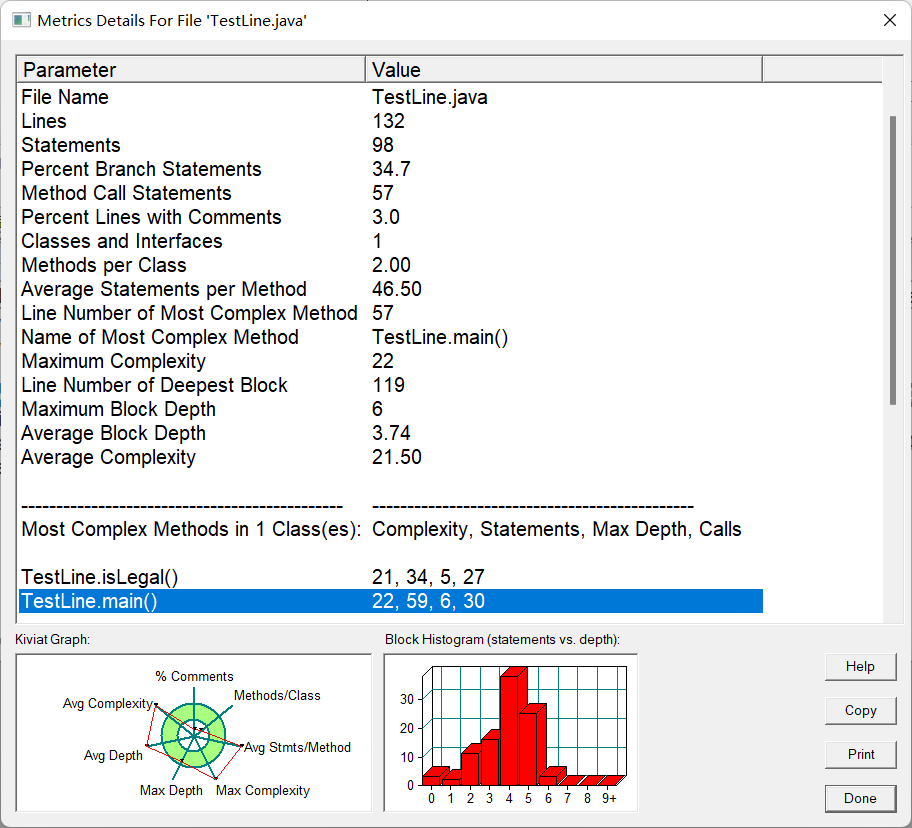
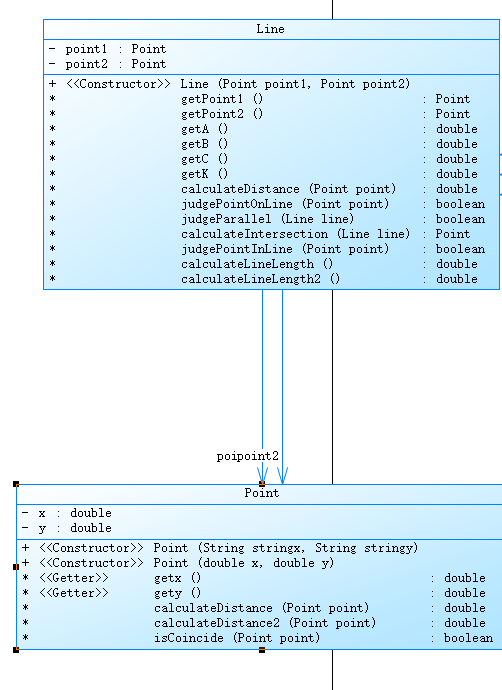
本题平均复杂度高达21.50，主要在于是TestPoint这个测试类，其中只含有main函数和isLegal函数。如果Point类和Line类单独看复杂度是不高的，但是对于测试类其中的if else 判断语句没有很好的解决方法。

7-3 点线形系列3-三角形的计算

用户输入一组选项和数据，进行与三角形有关的计算。选项包括：
1：输入三个点坐标，判断是否是等腰三角形、等边三角形，判断结果输出true/false，两个结果之间以一个英文空格符分隔。
2：输入三个点坐标，输出周长、面积、重心坐标，三个参数之间以一个英文空格分隔，坐标之间以英文","分隔。
3：输入三个点坐标，输出是钝角、直角还是锐角三角形，依次输出三个判断结果（true/false），以一个英文空格分隔，
4：输入五个点坐标，输出前两个点所在的直线与三个点所构成的三角形相交的交点数量，如果交点有两个，则按面积大小依次输出三角形被直线分割成两部分的面积。若直线与三角形一条线重合，输出"The point is on the edge of the triangle"
5：输入四个点坐标，输出第一个是否在后三个点所构成的三角形的内部（输出in the triangle/outof triangle）。
必须使用射线法，原理：由第一个点往任一方向做一射线，射线与三角形的边的交点（不含点本身）数量如果为1，则在三角形内部。如果交点有两个或0个，则在三角形之外。若点在三角形的某条边上，输出"on the triangle"

源码

import java.util.Scanner;

public class Main {

    
    /*用于判断输入是否合法
     * 合法就返回一个数组
     * 不合法就返回空
     */
    static String[] isLegal( String string) {
        String[] str = string.split(",| |:");
        if( !string.contains(":") || !string.contains(",") || !string.contains(" ")) {
            System.out.println("Wrong Format"); 
            return null;
        }
        if(string.charAt(string.length()-1) ==' ' || string.charAt(string.length()-1) ==':' || string.charAt(string.length()-1) ==','|| !str[0].matches("[12345]") ) {
            System.out.println("Wrong Format");
            return null;
        }
        for( int i = 1 ; i < str.length; i++) {
            if(!str[i].matches("[+-]?[1-9]\\d*(\\.\\d+)?|[+-]?[0](\\.\\d+)?")) {
                System.out.println("Wrong Format");
                return null;
            }
        }
        int len = Integer.parseInt(str[0]) ;
        if( len == 1 || len == 2 || len == 3) {
            if(string.split(" ").length + string.split(":").length - string.split(",").length == 1) {
                if( str.length != 7) {
                System.out.println("wrong number of points");
                return null;
                }
            }else {
                System.out.println("Wrong Format");
                return null;
            }
        }else if( len == 5) {
            if(string.split(" ").length + string.split(":").length - string.split(",").length == 1) {
                if( str.length != 9) {
                System.out.println("wrong number of points");
                return null;
                }
            }else {
                System.out.println("Wrong Format");
                return null;
            }
        }else if( len == 4 ) {
            if(string.split(" ").length + string.split(":").length - string.split(",").length == 1) {
                if( str.length != 11) {
                System.out.println("wrong number of points");
                return null;
                }
            }else {
                System.out.println("Wrong Format");
                return null;
            }
        }
        return str;
    }
    
    static void print(double num) {
        if( num * 1000000 % 1 != 0) {
            System.out.printf("%.6f",num);
        }else {
            System.out.print(num);
        }
    }
    
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        String s = sc.nextLine();
        if( isLegal(s) != null) {
            String[] str = isLegal(s) ;
            int len = Integer.parseInt(str[0]) ;
            if(len == 1) {
                Point p1 = new Point(str[1], str[2]);
                Point p2 = new Point(str[3], str[4]);
                Point p3 = new Point(str[5], str[6]);
                Line l12 = new Line(p1,p2);
                Line l13 = new Line(p1,p3);
                Line l23 = new Line(p2,p3);
                if( l12.judgePointOnLine(p3)|| p1.isCoincide(p2) || p1.isCoincide(p3) || p3.isCoincide(p2) ) {
                    System.out.println("data error");
                    System.exit(0);
                }else {
                    Triangle t = new Triangle(l12,l13,l23);
                    System.out.println(t.isIsoscelesTriangle() +" "+ t.isRegularTriangle());
                }
                
            }else if(len == 2) {
                Point p1 = new Point(str[1], str[2]);
                Point p2 = new Point(str[3], str[4]);
                Point p3 = new Point(str[5], str[6]);
                Line l12 = new Line(p1,p2);
                Line l13 = new Line(p1,p3);
                Line l23 = new Line(p2,p3);
                if( l12.judgePointOnLine(p3)|| p1.isCoincide(p2) || p1.isCoincide(p3) || p3.isCoincide(p2) ) {
                    System.out.println("data error");
                    System.exit(0);
                }else {
                    Triangle t = new Triangle(l12,l13,l23);
                    print(t.calculatePerimeter());
                    System.out.print(" ");
                    print(t.calculateArea());
                    System.out.print(" ");
                    print(t.calculateCore().getx());
                    System.out.print(",");
                    print(t.calculateCore().gety());
                }
            }else if(len == 3) {
                Point p1 = new Point(str[1], str[2]);
                Point p2 = new Point(str[3], str[4]);
                Point p3 = new Point(str[5], str[6]);
                Line l12 = new Line(p1,p2);
                Line l13 = new Line(p1,p3);
                Line l23 = new Line(p2,p3);
                if( l12.judgePointOnLine(p3)|| p1.isCoincide(p2) || p1.isCoincide(p3) || p3.isCoincide(p2) ) {
                    System.out.println("data error");
                    System.exit(0);
                }else {
                    Triangle t = new Triangle(l12,l13,l23);
                    System.out.println(t.isObtuseTriangle()+" "+t.isRightTriangle()+" "+t.isAcuteTriangle());
                }
            }else if(len == 4) {
                Point p1 = new Point(str[1], str[2]);
                Point p2 = new Point(str[3], str[4]);
                Point p3 = new Point(str[5], str[6]);
                Point p4 = new Point(str[7], str[8]);
                Point p5 = new Point(str[9], str[10]);
                Line l12 = new Line(p1,p2);
                Line l34 = new Line(p3,p4);
                Line l35 = new Line(p3,p5);
                Line l45 = new Line(p4,p5);
                if(p1.isCoincide(p2)) {
                    System.out.println("points coincide");
                    System.exit(0);
                }
                if( l34.judgePointOnLine(p5)|| p3.isCoincide(p4) || p3.isCoincide(p5) || p4.isCoincide(p5) ) {
                    System.out.println("data error");
                    System.exit(0);
                }else {
                    Triangle t = new Triangle(l34,l35,l45);
                    System.out.print(t.calculateIntersectionCount(l12));
                    if(t.calculateIntersectionCount(l12) == 2) {
                        //System.out.print(" ");
                        //print(t.calculateArea());
                        System.out.print(" ");
                        print(t.calculateCutArea(l12));
                        System.out.print(" ");
                        print(t.calculateArea()-t.calculateCutArea(l12));
                    }
                }
            }else if(len == 5) {
                Point p1 = new Point(str[1], str[2]);
                Point p2 = new Point(str[3], str[4]);
                Point p3 = new Point(str[5], str[6]);
                Point p4 = new Point(str[7], str[8]);
                Line l23 = new Line(p2,p3);
                Line l24 = new Line(p2,p4);
                Line l34 = new Line(p3,p4);
                if( l23.judgePointOnLine(p4)|| p2.isCoincide(p3) || p2.isCoincide(p4) || p3.isCoincide(p4) ) {
                    System.out.println("data error");
                    System.exit(0);
                }else {
                    /*  当点p1在三角形边所在直线上时
                     * 不足以说明p1在边上，可能是延长线上
                     *  所以同时判断点的x，y处于在该线段内两端的x，y范围中
                     *  此时就在三角形边上
                     */
                    if( l23.judgePointOnLine(p1)&&l23.judgePointInLine(p1) || l24.judgePointOnLine(p1)&&l24.judgePointInLine(p1) || l34.judgePointOnLine(p1)&&l34.judgePointInLine(p1)) {
                        System.out.println("on the triangle");
                        System.exit(0);
                    }else {
                        Triangle t = new Triangle(l23,l24,l34);
                        if( t.judgePointPlace(p1)) {
                            System.out.println("in the triangle");
                        }else {
                            System.out.println("outof the triangle");
                        }
                    }
                    
                    
                }
            }
                
        }
    }

}


class Triangle {
    private Line line12;  // 点一 与 点二 构成
    private Line line13;  // 点一 与 点三 构成
    private Line line23;  // 点二 与 点三 构成
    // 构造函数
    public Triangle(Line line1, Line line2, Line line3) {
        super();
        this.line12 = line1;
        this.line13 = line2;
        this.line23 = line3;
    }
    //判断三角形是否等腰
    boolean isIsoscelesTriangle() {  
        return line12.calculateLineLength() == line13.calculateLineLength() || line12.calculateLineLength() == line23.calculateLineLength() || line13.calculateLineLength() == line23.calculateLineLength() ;
    }
    //判断三角形是否等边
    boolean isRegularTriangle() {  
        return line12.calculateLineLength() == line13.calculateLineLength() && line12.calculateLineLength() == line23.calculateLineLength() ;
    }
    //  计算三角形周长
    double calculatePerimeter() {
        return line12.calculateLineLength()+line13.calculateLineLength()+line23.calculateLineLength();
    }
    /*
     *   根据三点计算三角形面积
     *   S=(1/2)*(x1y2+x2y3+x3y1-x1y3-x2y1-x3y2)  该公式存在方向性  A -> B -> C 
     *   由于方向上的未知  输出时加上绝对值abs
     */
    double calculateArea() {                          
        double num1 = line12.getPoint1().getx()*line12.getPoint2().gety() + line12.getPoint2().getx()*line13.getPoint2().gety() + line13.getPoint2().getx()*line13.getPoint1().gety() ;
        double num2 = line12.getPoint1().getx()*line13.getPoint2().gety() + line12.getPoint2().getx()*line13.getPoint1().gety() + line13.getPoint2().getx()*line12.getPoint2().gety() ;
        return Math.abs( (num1-num2)/2 ) ;  
    }
    // 计算三角形的重心
    Point calculateCore() {
        double x = ( line12.getPoint1().getx() + line12.getPoint2().getx() + line13.getPoint2().getx() ) / 3;
        double y = ( line12.getPoint1().gety() + line12.getPoint2().gety() + line13.getPoint2().gety() ) / 3;
        Point p = new Point(x,y);
        return p;
    }
    // 判断是否为钝角三角形
    boolean isObtuseTriangle() {
        double a = line12.calculateLineLength2() ;
        double b = line13.calculateLineLength2() ;
        double c = line23.calculateLineLength2() ;
        if(a > b && a > c ) {
            return a > b + c ;
        }else if(b > a && b > c ) {
            return b > a + c ;
        }else {
            return c > b + a ;
        }
    }
    // 判断是否为直角三角形
    boolean isRightTriangle() {
        double a = line12.calculateLineLength2() ;
        double b = line13.calculateLineLength2() ;
        double c = line23.calculateLineLength2() ;
        if(a > b && a > c ) {
            return a == b + c ;
        }else if(b > a && b > c ) {
            return b == a + c ;
        }else {
            return c == b + a ;
        }
    }
    // 判断是否为锐角三角形
    boolean isAcuteTriangle() {
        double a = line12.calculateLineLength2() ;
        double b = line13.calculateLineLength2() ;
        double c = line23.calculateLineLength2() ;
        if(a > b && a > c ) {
            return a < b + c ;
        }else if(b > a && b > c ) {
            return b < a + c ;
        }else {
            return c < b + a ;
        }
    }
    /*判断线是否与三角形的边重合
     * 先判断边是否与先平行
     * 若平行，在判断该平行边上的三角形上的端点是否在线上
     * 若在线上 则重合
     */
    boolean IsCoincideLine( Line line) {
        return  this.line12.judgeParallel(line) && line.judgePointOnLine(this.line12.getPoint1()) || this.line13.judgeParallel(line) && line.judgePointOnLine(this.line13.getPoint1()) || this.line23.judgeParallel(line) && line.judgePointOnLine(this.line23.getPoint1());
    }
    // 计算线与三角形交点数量
    int calculateIntersectionCount( Line line) {
        int count = 0;
        if( !this.line12.judgeParallel(line) ) {
            if( this.line12.judgePointInLine( this.line12.calculateIntersection(line) ) ) {
                count++;
            }
        }
        if( !this.line13.judgeParallel(line) ) {
            if( this.line13.judgePointInLine( this.line13.calculateIntersection(line) ) ) {
                count++;
            }
        }
        if( !this.line23.judgeParallel(line) ) {
            if( this.line23.judgePointInLine( this.line23.calculateIntersection(line) ) ) {
                count++;
            }
        }
        
        if( line.judgePointOnLine(this.line12.getPoint1()) || line.judgePointOnLine(this.line12.getPoint2()) || line.judgePointOnLine(this.line13.getPoint2()) ) {
            count--;
        }
        return count;
    }
    //
    // 射线法计算线与三角形交点数量
    //
    int calculateIntersectionCount2( Line line) {
        int count = 0;
        if( !this.line12.judgeParallel(line) ) {
            if( this.line12.judgePointInLine( this.line12.calculateIntersection(line) ) && this.line12.calculateIntersection(line).getx() > line.getPoint1().getx() ) {
                count++;
            }
        }
        if( !this.line13.judgeParallel(line) ) {
            if( this.line13.judgePointInLine( this.line13.calculateIntersection(line) ) && this.line13.calculateIntersection(line).getx() > line.getPoint1().getx() ) {
                count++;
            }
        }
        if( !this.line23.judgeParallel(line) ) {
            if( this.line23.judgePointInLine( this.line23.calculateIntersection(line) )&& this.line23.calculateIntersection(line).getx() > line.getPoint1().getx() ) {
                count++;
            }
        }
        
        if( line.judgePointOnLine(this.line12.getPoint1()) || line.judgePointOnLine(this.line12.getPoint2()) || line.judgePointOnLine(this.line13.getPoint2()) ) {
            count--;
        }
        return count;
    }
    /* 计算切割三角形后的两部分面积
     * 把面积小的部分传回去
     */
    double calculateCutArea( Line line) {
        if( line.judgePointOnLine(this.line12.getPoint1() ) ) {
            Line l1 = new Line( line.calculateIntersection(line23),this.line12.getPoint1() );
            Line l2 = new Line( line.calculateIntersection(line23), this.line13.getPoint2());
            Line l3 = new Line( this.line12.getPoint1() , this.line13.getPoint2());            
            Triangle t = new Triangle(l1,l2,l3);
            return Math.min( t.calculateArea() , this.calculateArea()-t.calculateArea() );
        }
        if( line.judgePointOnLine(this.line12.getPoint2() ) ) {
            Line l1 = new Line( line.calculateIntersection(line13),this.line12.getPoint2() );
            Line l2 = new Line( line.calculateIntersection(line13), this.line13.getPoint2());
            Line l3 = new Line( this.line12.getPoint2() , this.line13.getPoint2());            
            Triangle t = new Triangle(l1,l2,l3);
            return Math.min( t.calculateArea() , this.calculateArea()-t.calculateArea() );
        }
        if( line.judgePointOnLine(this.line13.getPoint2() ) ) {
            Line l1 = new Line( line.calculateIntersection(line12),this.line13.getPoint2() );
            Line l2 = new Line( line.calculateIntersection(line12), this.line12.getPoint2());
            Line l3 = new Line( this.line13.getPoint2() , this.line12.getPoint2());            
            Triangle t = new Triangle(l1,l2,l3);
            return Math.min( t.calculateArea() , this.calculateArea()-t.calculateArea() );
        }
        if( line.judgeParallel( this.line12 ) || !this.line12.judgePointInLine( this.line12.calculateIntersection(line) ) ) {
            Line l1 = new Line( line.calculateIntersection(line13), line.calculateIntersection(line23));
            Line l2 = new Line( line.calculateIntersection(line13), this.line13.getPoint2());
            Line l3 = new Line( line.calculateIntersection(line23), this.line13.getPoint2());            
            Triangle t = new Triangle(l1,l2,l3);
            return Math.min( t.calculateArea() , this.calculateArea()-t.calculateArea() );
        }else if( line.judgeParallel( this.line13 ) || !this.line13.judgePointInLine( this.line13.calculateIntersection(line) ) ) {
            Line l1 = new Line( line.calculateIntersection(line12), line.calculateIntersection(line23));
            Line l2 = new Line( line.calculateIntersection(line12), this.line12.getPoint2());
            Line l3 = new Line( line.calculateIntersection(line23), this.line12.getPoint2());            
            Triangle t = new Triangle(l1,l2,l3);
            return Math.min( t.calculateArea() , this.calculateArea()-t.calculateArea() );
        }else {  // 23
            Line l1 = new Line( line.calculateIntersection(line12), line.calculateIntersection(line13));
            Line l2 = new Line( line.calculateIntersection(line12), this.line13.getPoint1());
            Line l3 = new Line( line.calculateIntersection(line13), this.line13.getPoint1());            
            Triangle t = new Triangle(l1,l2,l3);
            return Math.min( t.calculateArea() , this.calculateArea()-t.calculateArea() );
        }
    }
    
    /*  判断第四个点坐标是否在后三个点所构成的三角形的内部
     * 内部返回true
     * 循环加数组产生八个不同方向的射线
     * 
     */
    boolean judgePointPlace( Point point) {
        int sum = 0;
        Point p = new Point( point.getx()+1 , point.gety() );
        Line l = new Line( point,p );
        sum += this.calculateIntersectionCount2(l);
        if( sum % 2 == 1 )
            return true;
        else
            return false;
    }
    
}



 class Line {

    private Point point1;
    private Point point2;    
    // 构造函数
    public Line(Point point1, Point point2) {
        super();
        this.point1 = point1;
        this.point2 = point2;
    }
    //  得到点一
    Point getPoint1() {
        return this.point1;
    }
    //  得到点二
    Point getPoint2() {
        return this.point2;
    }
    //  得到x的系数A
    double getA() {
        return point1.gety()-point2.gety();
    }
    //  得到y的系数B
    double getB() {
        return point2.getx()-point1.getx();
    }
    //  得到常数C
    double getC() {
        return point1.getx() * point2.gety() - point2.getx() * point1.gety();
    }
    //  得到直线的斜率K    
    double getK() {
        return (point1.gety()-point2.gety())/(point1.getx()-point2.getx());
    }
    // 计算点到直线的距离
    double calculateDistance( Point point) {       
        double a = Math.abs( this.getA()*point.getx() + this.getB()*point.gety() + this.getC());
        double b = Math.sqrt(this.getA() * this.getA() + this.getB()*this.getB());
        return a/b;
    }
    /* 判断三点是否共线
     * 或者判断点是否在直线上
     */
    boolean judgePointOnLine( Point point ){
        return this.getA()*point.getx()+this.getB()*point.gety()+this.getC() == 0;
    }
    // 判断两直线是否平行  平行返回true
    boolean judgeParallel( Line line ) {  
        if(this.getB() != 0 && line.getB() !=0)
            return this.getK() == line.getK() ;
        else if(this.getB() == 0 && line.getB() ==0){
            return true;
        }else {
            return false;
        }
    }
    
    // 计算线与线的交点
    Point calculateIntersection( Line line) {   
        double x = (line.getC()*this.getB()-this.getC()*line.getB())/(this.getA()*line.getB()-line.getA()*this.getB());
        double y = (line.getC()*this.getA()-this.getC()*line.getA())/(line.getA()*this.getB()-this.getA()*line.getB());
        if(x!=0 && y!=0 ) {
            Point point = new Point(x,y);return point;
        }            
        else if(x==0 && y==0 ) {
            Point point = new Point(0,0);return point;
        }            
        else if(x==0 && y!=0 ) {
            Point point = new Point(0,y);return point;
        }            
        else {
            Point point = new Point(x,0);return point;
        }    
    }
    // 判断交点是否在线段的内部(包括端点，若不想包含端点删掉 = 号即可)
    boolean judgePointInLine( Point point ) {   
        if( point.getx() <= Math.max( this.point1.getx(), this.point2.getx() ) && point.getx() >= Math.min( this.point1.getx() , this.point2.getx() ) && point.gety() <= Math.max( this.point1.gety(), this.point2.gety() ) && point.gety() >= Math.min( this.point1.gety() , this.point2.gety() ))
            return true;
        else
            return false;
    }
    //   计算线的长度
    double calculateLineLength() {        
        return this.point1.calculateDistance(this.point2);
    }
//  计算线的长度的平方
    double calculateLineLength2() {        
        return this.point1.calculateDistance2(this.point2);
    }
    

}


class Point {

    private double x;
    private double y;
    // 构造函数
    public Point(String stringx, String stringy) {
        this.x = Double.parseDouble(stringx) ;
        this.y = Double.parseDouble(stringy) ;
    }
    // 构造函数
    public Point(double x, double y) {   
        super();
        this.x = x;
        this.y = y;
    }
    //得到点的x坐标
    double getx() {               
        return this.x;
    }
    //得到点的y坐标
    double gety() {                    
        return this.y;
    }            
     //计算两点的距离
    double calculateDistance( Point point) { 
        double num = (this.x - point.x)*(this.x - point.x) + (this.y - point.y)*(this.y - point.y);
        return Math.sqrt(num);
    }
     //计算两点的距离的平方
        double calculateDistance2( Point point) { 
            return (this.x - point.x)*(this.x - point.x) + (this.y - point.y)*(this.y - point.y);
        }
    //判断两点是否重合
    boolean isCoincide( Point point) {    
        return this.x==point.x&&this.y==point.y;
    }

}

源码分析

和7-2一样超高的圈复杂度，还是由于测试类的mian方法和isLegal方法复杂度太高，不看测试类的话，Triangle和Line和Point类的平均复杂度基本都低于8，而我的测试类没有分开写很多的函数，而是一股脑全放在main中，导致main类的圈复杂度高达43，而我的判断输入语句是否合法的isLegal类由于不熟练正则表达式，导致圈复杂度很高。

踩坑心得

2-7-3 String的格式判断与内容提取

while( num < str.length() ){
            str1 = str.substring(num,num+8);
            if( str1.substring(0,6).equals("202017") || str1.substring(0,6).equals("202061")){
                if( num == str.length() - 8)
                    System.out.print(str1.substring(4,8));
                else
                    System.out.print(str1.substring(4,8)+" ");
            }
            num += 8;
        }

if( str1.substring(0,6).equals("202017") || str1.substring(0,6).equals("202061"))该if语句不能使用contains来判断是否含有特定字符串，因为特定字符串规定了只能在前六位，如果在后六位的话是不合法的
可是contains语句会判定为合法，所以此处使用substring来切割得到前六个进行对比。

3-7-1 点线形系列1-计算两点之间的距离

    public Point(String stringx, String stringy) {
        this.x = Double.parseDouble(stringx) ;
        this.y = Double.parseDouble(stringy) ;
    }
    // 构造函数
    public Point(double x, double y) {   
        super();
        this.x = x;
        this.y = y;
    }

采用了两个构造函数，在面对不同传参时都能产生点。

3-7-2 点线形系列2-线的计算

// 判断两直线是否平行
    boolean judgeParallel( Line line ) {  
        if(this.getB() != 0 && line.getB() !=0)
            return this.getK() == line.getK() ;
        else if(this.getB() == 0 && line.getB() ==0){
            return true;
        }else {
            return false;
        }
    }

此处不要使用斜率k来判断是否平行，因为当k不存在时考虑起来会特别麻烦。

// 判断交点是否在线段的内部
    boolean judgePointInLine( Point point ) {   
        if( point.getx() < Math.max( this.point1.getx(), this.point2.getx() ) && point.getx() > Math.min( this.point1.getx() , this.point2.getx() ) || point.gety() < Math.max( this.point1.gety(), this.point2.gety() ) && point.gety() > Math.min( this.point1.gety() , this.point2.gety() ))
            return true;
        else
            return false;
    }

进行判断时一定要同时判断在两点x值范围之间以及两点y值范围之间，不可单个考虑x或y，会有特殊情况导致过不去点。

3-7-3 点线形系列3-三角形的计算

/*
     *   根据三点计算三角形面积
     *   S=(1/2)*(x1y2+x2y3+x3y1-x1y3-x2y1-x3y2)  该公式存在方向性  A -> B -> C 
     *   由于方向上的未知  输出时加上绝对值abs
     */
    double calculateArea() {                          
        double num1 = line12.getPoint1().getx()*line12.getPoint2().gety() + line12.getPoint2().getx()*line13.getPoint2().gety() + line13.getPoint2().getx()*line13.getPoint1().gety() ;
        double num2 = line12.getPoint1().getx()*line13.getPoint2().gety() + line12.getPoint2().getx()*line13.getPoint1().gety() + line13.getPoint2().getx()*line12.getPoint2().gety() ;
        return Math.abs( (num1-num2)/2 ) ;  
    }

谨慎使用海伦公式，因为我在前面求线长的时候已经开过根号求线长，海伦公式在开根号，可能会导致误差过大，测试点过不去的情况。

改进建议

首先可改进一下我的正则表达式的部分，看似我使用了正则表达式，但没有使用到正则表达式的精髓，可自己写一个完整的正则表达式，删减掉我那些 if 判断语句，降低圈复杂度。
在3-7-1点的计算中，可把后面线的计算和三角形计算中关于点的判断伊西俄，全都放到点类中。
在3-7-3三角形的计算中，可以把许多在方法中的与或非判断，整合到一个方法中，既可以降低圈复杂度，还可以提高代码的复用性，后期好维护。
在3-7-3三角形计算中计算线与三角形交点数量的方法与射线法计算线与三角形交点数量的方法我感觉可以整合成一个方法，可是我还没有想到怎么做。

总结

对于这个阶段的三次作业，我对于Java中字符串的处理有了进一步更深的了解。也开始掌握并熟练使用正则表达式来控制输入的合法性。在编写这三次作业中，尤其的第三次作业，老师

故意把一个大题，分成了三个小题，锻炼了我的面对对象的程序思维。我注意到，在使用面对对象的成语语言编写代码时，可以明显的降低代码的重复性，提升代码的可读性。我在第三次

作业中有意的采用了面对对象的语言结构，也对其中的数据进行了封装。但是在整合出一个测试类时，我明显能感觉到我又有一种面对过程的编写习惯。在以后的作业中我希望我自己可以

养成面对对象编程的习惯。

posted @ 2022-10-02 14:03 昌航小迷弟七号阅读(32) 评论(1) 收藏举报

刷新页面返回顶部

HelloWorldjava