斜率优化 DP

斜率优化 DP

代数意义

对于一个式子：\(\displaystyle f_i = \min_{j < i} (f_j + a_i \times b_j)\)，其中 \(a_i, b_i\) 单调递增。

考虑对于两个位置 \(x, y\)，若 \(f_x + a_i \times b_x \le f_y + a_i \times b_y\)，则 \(x\) 比 \(y\) 优。
移项，得 \(\frac{f_x - f_y}{b_x - b_y} \le -a_i\).

将所有 \((b_i, f_i)\) 加入坐标系，通过对斜率进行比较，可以找到最优的点。

可以发现，每次的决策点一定都在下凸壳上，现在考虑证明。

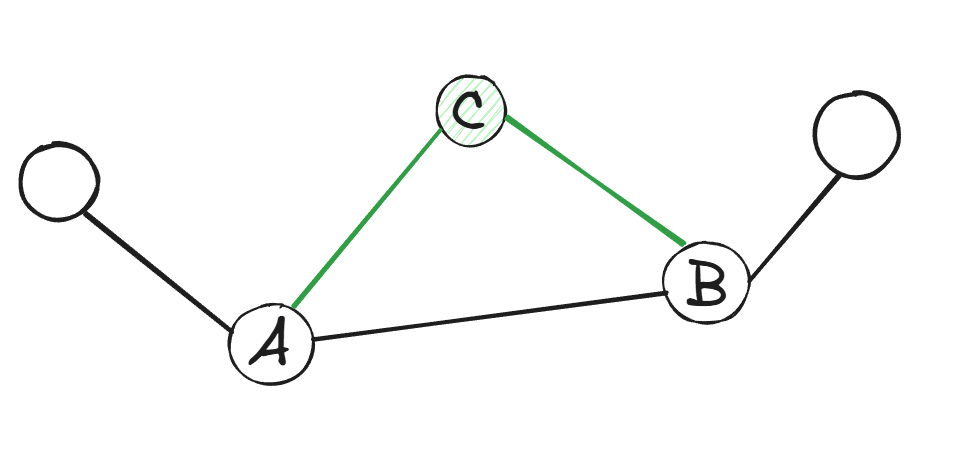
考虑在凸壳上的点 \(A, B\) 和内部一点 \(C\)，设当前询问的斜率为 \(k'\)，分类讨论：

• 若 \(k' \le k_{AC} \le k_{BC}\)，则 \(A\) 优于 \(C\)，\(C\) 优于 \(B\)；
• 若 \(k_{AC} \le k' \le k_{BC}\)，则 \(B\) 优于 \(C\)，\(A\) 优于 \(C\)；
• 若 \(k_{AC} \le k_{BC} \le k'\)，则 \(B\) 优于 \(C\)，\(C\) 优于 \(A\).

容易发现，无论如何 \(C\) 都不会成为最优转移点，所以可以直接删掉，只留下凸壳上的点。

每次确定决策点相当于用一条直线截凸壳，最优点一定是直线与凸壳的切点。
（在横坐标单增的情况下，每次的决策点其实就是每次左边删去所有满足 \(q_i\) 不优于 \(q_i+1\) 的 \(q_i\) 之后，凸壳最靠左的点；若横坐标不单调，就要通过二分找到决策点）

注意到在下凸壳上斜率递增，同时 \(-a_i\) 也单调递减，所以考虑在 \(i\) 从 \(1\) 移动到 \(n\) 的过程中，使用单调队列动态维护凸壳中每一条边，当斜率大于 \(k'\) 时弹出。

几何意义（常用）

对一个点 \((b_x, f_x)\)，取一条斜率为 \(-a_i\) 的直线，则直线可表示为 \(f_x = -a_i \cdot b_x + B\).

移项，得 \(B = f_x + a_i \cdot b_x\)，即为转移式中的权值。

故转移式中的权值最小，就转化为了使 \(B\) 最小。

而注意到 \(B\) 是直线 \(f_x = -a_i \cdot b_x + B\) 在 \(y\) 轴上的截距。相当于固定了一些点 \((b_x, f_x)\)，要找到一条斜率为 \(-a_i\) 的直线使得截距 \(B\) 最小。

仍然可以发现这样会截在下凸壳上，于是其余部分和代数意义的理解是相同的。

李超树优化

将代数意义中的 \(f_x + a_i \times b_x \le f_y + a_i \times b_y\) 分别看做两条以 \(b_x, b_y\) 为斜率的直线，考虑用李超树维护这些直线，每次相当于查找某个横坐标上所有直线最小的纵坐标。

LG5785 [SDOI2012] 任务安排

题目链接：https://www.luogu.com.cn/problem/P5785

使用代数意义去理解，把 DP 产生的一些后面的贡献加在 \(dp_i\) 上，转移式是 \(\displaystyle dp_i \gets \min_{j = 1}^{i - 1} \left\{dp_j + s \times \sum_{k = j}^n f_j + \left(\sum_{k = 1}^i t_k\right) \times \left(\sum_{k = j + 1}^i f_i\right)\right\}\).

#include <bits/stdc++.h>
using namespace std;

#define int long long
const int N = 3e5 + 5;

int n, s, t[N], c[N], st[N], sc[N], q[N], head = 1, tail, x[N], y[N], f[N];

int find(int k, int l, int r)
{
	int p = r;
	while(l <= r)
	{
		int mid = (l + r) >> 1;
		if(y[q[mid + 1]] - y[q[mid]] > k * (x[q[mid + 1]] - x[q[mid]])) p = mid, r = mid - 1;
		else l = mid + 1;
	}
	return q[p];
}

signed main()
{
	ios :: sync_with_stdio(false);
	cin.tie(0), cout.tie(0);
	cin >> n >> s;
	for(int i = 1; i <= n; i++)
		cin >> t[i] >> c[i], st[i] = st[i - 1] + t[i], sc[i] = sc[i - 1] + c[i];
	// f[i] = f[j] + s * (sc[n] - sc[j]) + st[i] * (sc[i] - sc[j])
	// j 优于 k
	// f[j] - s * sc[j] - st[i] * sc[j] < f[k] - s * sc[k] - st[i] * sc[k]
	// f[j] - f[k] < (st[i] + s) * (sc[j] - sc[k])
	// (f[j] - f[k]) / (sc[j] - sc[k]) < st[i] + s
	q[++tail] = 0;
	for(int i = 1; i <= n; i++)
	{
		int j = find(s + st[i], head, tail);
		f[i] = f[j] + s * (sc[n] - sc[j]) + st[i] * (sc[i] - sc[j]);
		x[i] = sc[i], y[i] = f[i];
		while(head < tail && (y[q[tail - 1]] - y[q[tail]]) * (x[q[tail]] - x[i]) >= (x[q[tail - 1]] - x[q[tail]]) * (y[q[tail]] - y[i])) tail--;
		q[++tail] = i;
	}
	cout << f[n];
	return 0;
}

上面的所有讨论都是针对 DP 式子中有 \(\min\) 的情况，若为 \(\max\) 则最优转移点一定在上凸壳上，证明类似下凸壳的情况。

可以认为，维护上凸壳的代码基本就是维护下凸壳的代码所有符号反过来。