组合数学相关
一. 组合数递推公式:
𝐶_𝑛^𝑚=𝐶_(𝑛−1)^(𝑚−1)+𝐶_(𝑛−1)^𝑚
C(n,m) = C(n-1,m)+C(n-1,m-1);
二. 鸽笼原理
描述:
如果n个物体被放进m个盒子,那么至少有一个盒子有⌈𝑛/𝑚⌉个物体。 -->意思为向上取整,用floor函数可以实现
经典案例:
对数列a1,a2,a3,……an,至少存在1≤i<j≤n,使得∑1_(𝑘=𝑖)^𝑗 𝑎_𝑘 能被n整除。 -->即ai+..+aj 能被n整除。
证明如下:
作和函数 S1 = a1;S2 = a1+a2... ;Sn = a1+a2+a3+..+an; 假设这n个数不能被n整除,则余数的域为1--n-1,
这就相当于把n-1个数放进n个笼子,肯定有两个余数相等,则肯定有Sj - Si 能被n整除。
三. 容斥原理
几个集合并集的大小=所有单个集合的大小之和-(所有任意)两个的交+(所有任意)三个的交-(所有任意)四个的交……
比如𝐴∪𝐵∪𝐶 = 𝐴+𝐵+𝐶−𝐴∩𝐵−𝐴∩𝐶−𝐵∩𝐶+𝐴∩𝐵∩𝐶。
四.Ramsey定理
定义 Kn 表示 n 个点的完全图,对于给定的 n 和 m,存在一个最小的正整数 p 使得将 Kp 的边分别染上红 色或蓝色后,一定存在一个 Kn 子图是红色或者一个 Km 子 图是红色,并且对于更大的任意 p 都成立,这样的 p 记作 r(n,m)。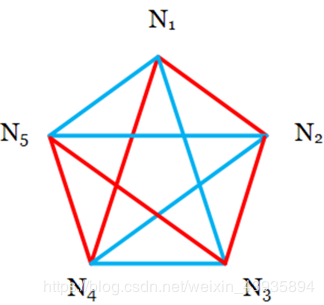
例题
CCPC 2016 Changchun G Instability
给定一个 n 点 m 边的无向图 (n ≤ 50),问有多少点集满足要 么存在三个点两两相连,要么存在三个点两两不相连
思路:
根据Ramsey 定理,可得r(3,3)=6 ,所以6元及以上集合必然有三元完全子图。只需暴力跑一遍5元集以下即可
#include <iostream> #include <cstdio> #include <cstring> using namespace std; typedef long long ll; const int N=105; const int mod=1e9+7; int fac[N],fnv[N]; int n,m; int rec[10]; bool groud[N][N]; ll ans; ll C(int x,int y) { if(x<y) return 0; return 1ll*fac[x]*fnv[y]%mod*fnv[x-y]%mod; } ll quickmod(ll x,ll y) { ll ans=1; for(;y;y>>=1) { if(y&1) ans=ans*x%mod; x=x*x%mod; } return ans; } void getf() { fac[0]=1; for(int i=1;i<N;i++) fac[i]=1ll*fac[i-1]*i%mod; fnv[N-1]=quickmod(fac[N-1],mod-2); for(int i=N-2;i>=0;i--) fnv[i]=1ll*fnv[i+1]*(i+1)%mod; } void dfs(int x,int y) { if(x==6) return; for(int i=y+1;i<=n;i++) { rec[x]=i; if(x>=3) { bool flag=false; for(int p1=1;p1<x-1;p1++) { for(int p2=p1+1;p2<x;p2++) { for(int p3=p2+1;p3<=x;p3++) { if(groud[rec[p1]][rec[p2]] && groud[rec[p2]][rec[p3]]&& groud[rec[p3]][rec[p1]]) { ans++; flag=true; break; } else if(!groud[rec[p1]][rec[p2]] && !groud[rec[p2]][rec[p3]]&& !groud[rec[p3]][rec[p1]]) { ans++; flag=true; break; } } if(flag) break; } if(flag) break; } } dfs(x+1,i); } } int main() { getf(); int T; scanf("%d",&T); for(int no=1;no<=T;no++) { scanf("%d%d",&n,&m); memset(groud,false,sizeof(groud)); int x,y; for(int i=0;i<m;i++) { scanf("%d%d",&x,&y); groud[x][y]=groud[y][x]=true; } ans=quickmod(2,n); for(ll i=0;i<=5;i++) { ans=(ans-C(n,i)+mod)%mod; } dfs(1,0); printf("Case #%d: %lld\n",no,ans); } return 0; }
五.卡特兰数
卡特兰数是一种经典的组合数,经常出现在各种计算中
公式 h(n) = h(0) * h(n-1)+h1h(n-2)+ …+h(n-1)h(0)
一般式 h(n) = C(2n,n)/(n+1)
另类递推公式:C(n)=C(n-1)((4*n-2)/(n+1));
应用
长度为2*n的0 1序列,要求0的个数与1的个数相同,并且满足在任意位置,序列的前缀中0的个数不多于1的个数。
括号匹配
进出栈顺序
在圆上选择2n个点,将这些点成对连接起来,使得所得到的n条线段不相交的方法数
给定N个节点,能构成多少种形状不同的二叉树
六.第一类斯特林
表示将 n 个不同元素构成m个圆排列的数目
公式 s(n , m) = s(n-1 , m-1) + n*s(n-1 , m)
考虑第n个元素放哪
例题 有n个仓库,每个仓库有两把钥匙,共2n把钥匙。同时又有n位官员。问如何放置钥匙使得所有官员都能够打开所有仓库?
将官员分成m组,每组能打开且只能打开本组的仓
七.第二类斯特林数
表示将n个不同的元素拆分成m个集合的方案数
公式 s(n , m) = s(n-1 , m-1) + m*s(n-1 , m)
同理 考虑 第n个元素放哪
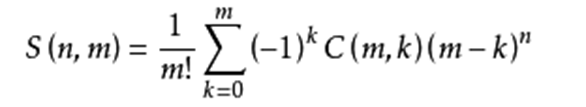


 浙公网安备 33010602011771号
浙公网安备 33010602011771号