洛谷P10533 [Opoi 2024] 热核武器 (本蒟蒻第一篇题解)
[Opoi 2024] 热核武器
题目背景
跳蚤国与蛐蛐国正在激战!
上面是战术核显卡,与题目没有关联。
题目描述
跳蚤国的国土可以看作平面直角坐标系。
跳蚤国有 \(N+1\) 座城市,有 \(1\) 座是首都,位于 \((0,0)\),另 \(N\) 座是普通城市,在这里假设首都为 \(0\) 号城市,其他城市编号为 \(1\) 至 \(N\),对于每一座普通城市,位于 \((x_i,y_i)\)。
由于跳蚤国财力有限,对于每一个不是首都的城市 \(i\),它会选择一个城市 \(j\) 修建一条双向公路。令 \(dis(x,y)\) 为 \(x\),\(y\) 城市的欧几里得距离,则对于每一个不是首都的城市 \(i\),它所对应的 \(j\) 则是满足 \(dis(j,0) \le dis(i,0)\) ,\(j \ne i\) 的所有点中 \(dis(i,j)\) 最小的点,如有多个合法 \(j\),取其中编号最小的一个。
定义一座城市的 \(\gamma\) 值为这个城市走到首都所需要的最小道路数 \(+1\),如果走不到首都,设 \(\gamma\) 值为 \(0\)。
蛐蛐国要对跳蚤国进行战术核显卡打击,这次行动分为两个组:洛伦兹组和安培组。每个组都要对跳蚤国的部分城市进行打击,其中两个组需要恰好把跳蚤国每个城市打击一遍。
对于这两个组来说,名利是最重要的,而蛐蛐国的评功标准是按照本次行动所打击城市的 \(\gamma\) 值和。所以你需要求出:有没有一种划分方式使得洛伦兹组和安培组分别的打击城市的 \(\gamma\) 值和相等,可以,输出 Yes,否则输出 No 。
输入格式
第 \(1\) 行输入一个整数 \(N\),表示跳蚤国普通城市的数目。
接下来第 \(2 \sim N+1\) 行,第 \(i+1\) 行输入两个整数,表示第 \(i\) 座城市的横纵坐标 \((x_i,y_i)\)。
输出格式
一行一个字符串,Yes 或者 No。表示是否会有一种方法使得洛伦兹组和安培组分别的打击城市的 \(\gamma\) 值和相等。
样例 #1
样例输入 #1
4
-1 -1
1 0
1 -2
-2 2
样例输出 #1
Yes
提示
样例解释
这幅图是长这样的:
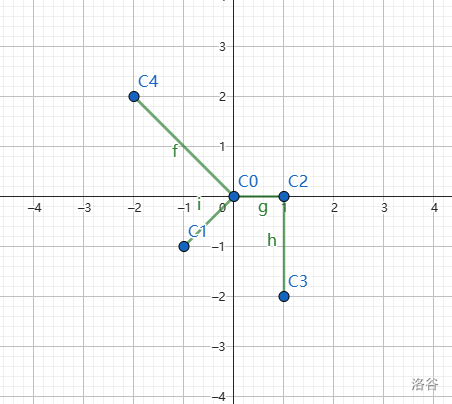
对于 \(C1\),\(C0\) 和 \(C2\) 满足 \(dis(j,0) \le dis(C1,0)\),但是 \(C0\) 离 \(C1\) 距离更近,添加边 \((C1,C0)\)。
对于 \(C2\),只有 \(C0\) 满足 \(dis(j,0) \le dis(C2,0)\),添加边 \((C2,C0)\)。
对于 \(C3\),\(C0\),\(C1\) 和 \(C2\) 满足 \(dis(j,0) \le dis(C3,0)\),但是 \(C2\) 离 \(C3\) 距离最近,因此添加边 \((C3,C2)\)。注意这里是因为在 \(C3\) 处考虑时,最优点为 \(C2\),所以 \(C3\) 才向 \(C2\) 修建了一条公路,和公路 \((C2,C0)\) 完全独立。
对于 \(C4\),其他所有点都满足 \(dis(j,0) \le dis(C4,0)\),但是 \(C0\) 离 \(C4\) 距离最近,添加边 \((C4,C0)\)。
得到下面的表:
| 城市编号 | \(\gamma\) 值 |
|---|---|
| 0 | 1 |
| 1 | 2 |
| 2 | 2 |
| 3 | 3 |
| 4 | 2 |
所以把 \(0,1,2\) 分给洛伦兹组,\(3,4\) 分给安培组即可。
数据范围
\(1 \le N \le 500\),\(-10^6 \le x_i,y_i \le 10^6\)。
特殊说明
由于本题输出只有 Yes 和 No,所以本题采用最小分值评测法,即取所有测试点的得分最小值作为结果。
题目解答
问题简单分析
- 构建图:
- 城市编号从
0(首都)到N。 - 对于每个普通城市
i(1 ≤ i ≤ N),找到满足dis(j, 0) ≤ dis(i, 0)且j ≠ i的城市j中距离i最近的城市。如果有多个,选择编号最小的j。 - 添加双向公路
(i, j),(j, i)。
- 城市编号从
- 计算 γ 值:
- 对于每个城市,计算从首都到该城市的最小道路数
d,则γ = d + 1。 - 如果无法到达首都,
γ = 0。
- 对于每个城市,计算从首都到该城市的最小道路数
- 划分城市:
- 将所有城市划分为俩个组,使得两个组的
γ值和相等。 - 判断是否存在这样的划分方式。
- 将所有城市划分为俩个组,使得两个组的
解决思路
-
构建图
- 使用邻接表来表示城市之间的连接。
- 使用 广度优先搜索(BFS) 来计算从首都到每个城市的最短道路数。
-
计算 γ 值
- 初始化所有城市的 γ 值为
0。 - 对于能到达首都的城市,γ 值为最短路径长度加
1。
- 初始化所有城市的 γ 值为
-
划分城市并判断可行性
- 这是一个经典的 划分问题,目标是将 γ 值分为两部分,使得两部分的和相等。
- 使用 动态规划(DP)(利用位运算优化)来判断是否存在这样的划分。
-
特殊考虑
- 城市的坐标可能较大,因此在计算距离时,使用 长整型(
long long) 避免整数溢出。 - 由于传送门数量和城市数量较大,需优化代码以满足时间和空间要求。(利用位运算对动态规划(
dp)进行优化)
- 城市的坐标可能较大,因此在计算距离时,使用 长整型(
代码逐步实现:
前置代码
#include <bits/stdc++.h>
using namespace std;
using ll = long long; // long long太长,直接 ll 代替
- 城市结构与距离计算:
- 定义了
city结构体来存储每个城市的坐标。 - 使用
dist函数计算两个城市之间的欧几里得距离的平方,避免使用浮点数。
- 定义了
// 定义城市结构,包含坐标
struct city {
ll x;
ll y;
};
// 计算两个城市之间的欧几里得距离的平方
ll dist(const city& a, const city& b) {
ll dx = a.x - b.x;
ll dy = a.y - b.y;
return dx * dx + dy * dy;
}
- 构建邻接表:
- 对于每个普通城市
i(1 ≤ i ≤ N),遍历所有可能的城市j(0 ≤ j ≤ N,j ≠ i),找到满足dis(j,0) <= dis(i,0)的j中距离i最近的城市。如果有多个,选择编号最小的j。 - 将
i和j之间添加双向边。
- 对于每个普通城市
// 构建邻接表
vector<vector<int>> adj(N + 1, vector<int>());
for(int i = 1; i <= N; i ++)
{
ll min = LLONG_MAX; // LLONG_MAX = 2 ^ 63 - 1
int sj = -1;
for(int j = 0; j <= N; j ++)
{
if(j == i) continue; // 满足 dis(j,0) <= dis(i,0)
if(cap[j] <= cap[i])
{
ll ij = dist(cities[i], cities[j]);
if(ij < min)
{
min = ij;
sj = j;
}
else if(ij == min && j < sj)
sj = j;
}
}
if(sj != -1)
{
adj[i].push_back(sj);
adj[sj].push_back(i);
}
}
- 广度优先搜索(BFS)计算最短路径:
- 从首都(城市
0)开始进行 BFS,计算每个城市到首都的最短道路数。 distance_bfs[i]存储城市i到首都的最短道路数,未访问的城市保持-1。
- 从首都(城市
// BFS 从首都 (0) 开始,计算最短路径
vector<int> dist_bfs(N+1, -1); // -1 表示未访问
queue<int> q;
q.push(0);
dist_bfs[0] = 0;
while(!q.empty())
{
int u = q.front(); q.pop();
for(auto &v: adj[u])
if(dist_bfs[v] == -1)
{
dist_bfs[v] = dist_bfs[u] + 1;
q.push(v);
}
}
-
计算 γ 值:
-
对于每个城市
i,如果dist_bfs[i]不等于-1,则γ[i] = dist_bfs[i] + 1;否则,γ[i] = 0。 -
将所有 γ 值大于
0的城市存入gv向量。
-
-
动态规划实现:
- 初始化
dp为 0,表示初始子集和为 0。 - 对于每个 γ 值 g,将
dp左移 g 位后与原dp进行 OR 操作,表示在现有子集和基础上加入 g 后可能的子集和。 - 最终检查
dp[target] 是否为 1,即是否存在子集和为 target。
- 初始化
-
输出结果:
- 如果存在这样的划分,输出 Yes;否则,输出 No。
// 计算 γ 值
vector<int> g(N + 1, 0); // g[0] 表示首都
for(int i = 0; i <= N; i ++)
if(dist_bfs[i] != -1) g[i] = dist_bfs[i] +1;
else g[i] = 0;
// 收集所有 γ 值
vector<int> gv;
for(int i = 0; i <= N; i ++)
if(g[i] > 0) gv.push_back(g[i]);
// 计算总和
ll total_sum = 0;
for(auto &g: gv)
total_sum += g;
// 如果总和为奇数,则不可能平分
if(total_sum % 2 !=0)
{
cout << "No\n";
return 0;
}
ll target = total_sum / 2;
// 使用位运算优化的动态规划实现
// 由于 target 可能高达 500*500=250,000,我们使用 bitset
// C++ 的 bitset 不能动态定义大小较大,一般最大到几百万
// 这里 target <= 250,000,可以使用 bitset<250001>
const int MAX_SUM = 250001;
if(target > MAX_SUM)
{
// 由于 N <=500, gamma_i <= 1000
cout << "No\n";
return 0;
}
bitset<250001> dp;
dp[0] = 1;
for(auto &g: gv) dp |= (dp << g);
if(target <= 250000 && dp[target]) cout << "Yes\n";
else cout << "No\n";
完整代码:
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
// 定义城市结构,包含坐标
struct city {
ll x;
ll y;
};
// 计算两个城市之间的欧几里得距离的平方
ll dist(const city& a, const city& b) {
ll dx = a.x - b.x;
ll dy = a.y - b.y;
return dx * dx + dy * dy;
}
int main(){
ios::sync_with_stdio(false);
cin.tie(0);
int N;
cin >> N;
// 城市编号从 0 到 N,城市 0 是首都 (0,0)
vector<city> cities(N + 1, City{0, 0});
for(int i = 1; i <= N; i ++){
cin >> cities[i].x >> cities[i].y;
}
// 预计算每个城市到首都的距离平方
vector<ll> cap(N + 1, 0);
for(int i = 0; i <= N; i ++)
cap[i] = dist(cities[i], cities[0]);
// 构建邻接表
vector<vector<int>> adj(N + 1, vector<int>());
for(int i = 1; i <= N; i ++)
{
ll min = LLONG_MAX;
int sj = -1;
for(int j = 0; j <= N; j ++)
{
if(j == i) continue;
// 满足 dis(j,0) <= dis(i,0)
if(cap[j] <= cap[i])
{
ll ij = dist(cities[i], cities[j]);
if(ij < min)
{
min = ij;
sj = j;
}
else if(ij == min && j < sj)
sj = j;
}
}
if(sj != -1)
{
adj[i].push_back(sj);
adj[sj].push_back(i);
}
}
// BFS 从首都 (0) 开始,计算最短路径
vector<int> dist_bfs(N+1, -1); // -1 表示未访问
queue<int> q;
q.push(0);
dist_bfs[0] = 0;
while(!q.empty())
{
int u = q.front(); q.pop();
for(auto &v: adj[u])
if(dist_bfs[v] == -1)
{
dist_bfs[v] = dist_bfs[u] + 1;
q.push(v);
}
}
// 计算 γ 值
vector<int> g(N + 1, 0); // g[0] 表示首都
for(int i = 0; i <= N; i ++)
if(dist_bfs[i] != -1) g[i] = dist_bfs[i] +1;
else g[i] = 0;
// 收集所有 γ 值
vector<int> gv;
for(int i = 0; i <= N; i ++)
if(g[i] > 0) gv.push_back(g[i]);
// 计算总和
ll total_sum = 0;
for(auto &g: gv)
total_sum += g;
// 如果总和为奇数,则不可能平分
if(total_sum % 2 !=0)
{
cout << "No\n";
return 0;
}
ll target = total_sum / 2;
// 使用位运算优化的动态规划实现
// 由于 target 可能高达 500*500=250,000,我们使用 bitset
// C++ 的 bitset 不能动态定义大小较大,一般最大到几百万
// 这里 target <= 250,000,可以使用 bitset<250001>
const int MAX_SUM = 250001;
if(target > MAX_SUM)
{
// 由于 N <=500, g_i <= 1000
cout << "No\n";
return 0;
}
// 代码解释:这里 bitset<250001> dp 创建了一个大小为 250001 的位集(全部初始化为 0),然后将 dp[0] 设为 1,表示可以凑成0
bitset<250001> dp;
dp[0] = 1;
// 代码解释:假设我们有一个整数数组 nums,目标是找到一些子集使总和为某一值。通过位移操作 dp << num,我们将当前状态集合 dp 中所有为1的位置向左移动 num 位,并将结果与原来的 dp 进行或运算 |=, 来更新状态。
for(auto &g: gv) dp |= (dp << g);
if(target <= 250000 && dp[target]) cout << "Yes\n";
else cout << "No\n";
return 0;
}
示例验证:
输入:
4
-1 -1
1 0
1 -2
-2 2
执行过程:
- 构建图后,连接关系为:
- 城市 1 连接城市 0
- 城市 2 连接城市 0
- 城市 3 连接城市 2
- 城市 4 连接城市 0
- 计算 γ 值:
- γ[0] = 1
- γ[1] = 2
- γ[2] = 2
- γ[3] = 3
- γ[4] = 2
- γ 值总和为
1 + 2 + 2 + 3 + 2 = 10,目标子集和为5。 - 检查是否存在子集和为
5:- 存在子集
{2, 3},其和为5。
- 存在子集
输出:
Yes
本蒟蒻的第一篇题解完结OvO
想多了都是问题,做多了都是答案,愿每一位努力的同学都不负梦想,与大家共勉.


 浙公网安备 33010602011771号
浙公网安备 33010602011771号