CF1276B Two Fair(BFS)

Two Fairs

题目大意：

• 给出一张有 \(n\) 个结点、 \(m\) 条边的无向联通图；
• 图上有两个特殊点 \(a\) 和 \(b\) （\(1\leq a,b\leq n,\ a\neq b\)）；
• 求出满足下列条件的二元组 \((u,v)\) 的对数：
  • \(1\leq u < v\leq n\)；
  • \(u\neq a,v\neq a,u\neq b,v\neq b\)
  • 任意一条从 \(u\) 到 \(v\) 的路径 \((u,e_1,e_2,...,e_k,v)\) 都经过 \(a\) 和 \(b\) 。

思路:

  找出一条路径使得要经过\(a,b\)两点,先将图画出来.

  对于这张图来说，就是要选择\(a\)左侧的\(1, 2, 3\)和\(b\)右侧的\(8, 9, 10\)这些点作为起始点拉出一条路径，这样一定会经过\(a,b\)两点。

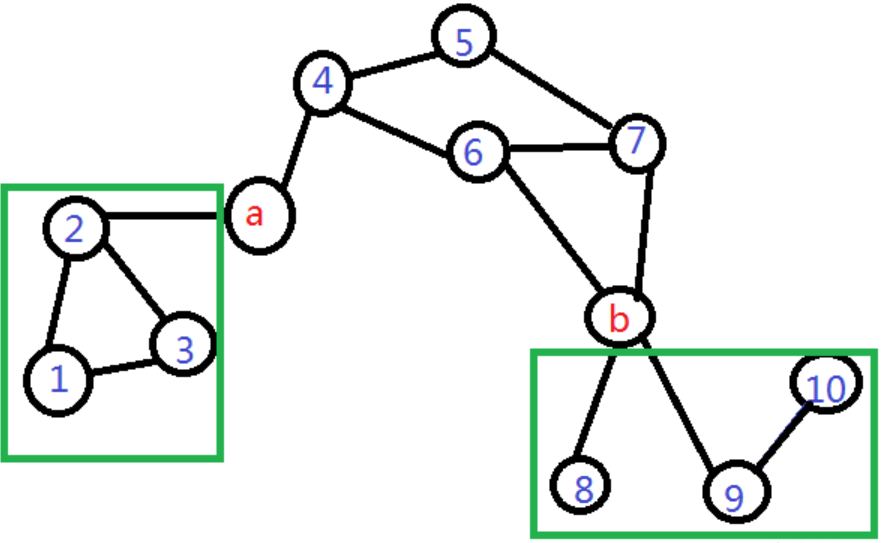
  接下来就是要想办法处理出来\(a,b\)两端的点,可以考虑用\(bfs\)来将这些点搜索出来,每一次搜索都将\(a,b\)两点打上标记。

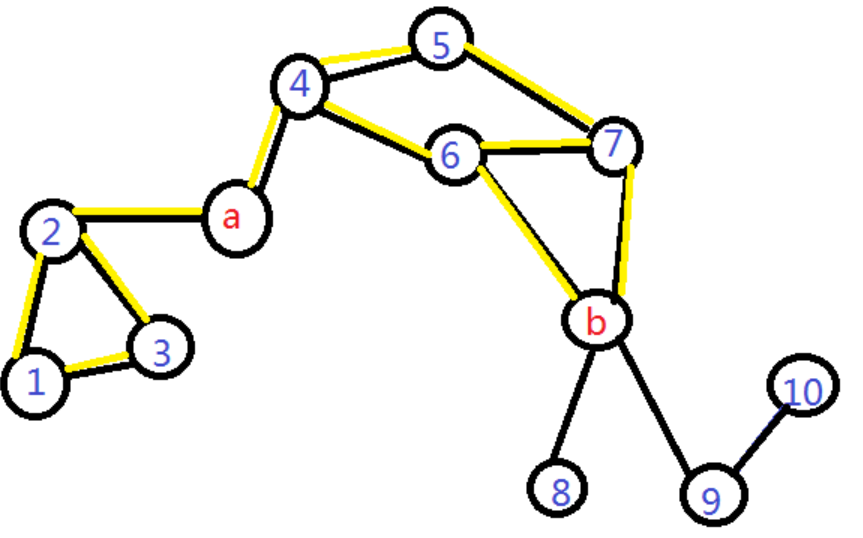
这样分别以\(a,b\)为起点搜索两次就可以得到两边的点是哪些。得到了两侧的点,剩下的答案统计就是一个乘法计数原理了.\(ans = a×b\)。

    void solve() {
        int n, m, a, b;
        std::cin >> n >> m >> a >> b;
        std::vector<std::vector<int>> adj(n + 1);
        for (int i = 0; i < m; i++) {
            int u, v;
            std::cin >> u >> v;
            adj[u].emplace_back(v);
            adj[v].emplace_back(u);
        }

        auto bfs = [&](int s) -> int {
            std::queue<int> q;
            q.push(s);
            std::vector<bool> vis(n + 1);
            vis[a] = vis[b] = true;

            while(q.size()) {
                int u = q.front();
                q.pop();
                for (auto& v : adj[u]) {
                    if (!vis[v]) {
                        vis[v] = true;
                        q.push(v);
                    }
                }
            }

            int ans = 0;
            for (int i = 1; i <= n; i++) ans += !vis[i];
            return ans;
        };

        int A = bfs(a), B = bfs(b);
        std::cout << 1ll * A * B << "\n";
    }