2019ICPC南京[补题]

C

题目大意：

  给我们一张网格图，我们求出所有的路径使得这个路径至少包括四个点，且这四个点是严格递增且相邻两个点的差值为\(1\),并且这条路径如果能走就必须走到不能走为止。

解题思路：

  考虑从起点开始走一直走到最后的话，会有\(dfs\)和\(bfs\)两种想法，但是如果是用\(bfs\)的话，统计终点的方案不是很好进行操作，所以采用\(dfs\)回溯的方式来解决。我们可以从每一个点开始搜一遍，一直走到终点然后从终点开始往回走，统计这条路径起点处的方案数，这样即使是有多条路径共一个起点的情况，也不会有重复和错漏的情况。

代码：

点击查看代码

    int n, m;
    int a[N][N];
    bool vis[N][N];
    i64 ans[N][N][4];
     
    int dx[] = {0, 1, 0, -1};
    int dy[] = {1, 0, -1, 0};
     
    void dfs(int x, int y) {
    	vis[x][y] = 1;
    	int cnt = 0;
    	rep(i, 0, 4) {
    		int xx = x + dx[i], yy = y + dy[i];
    		if (xx < 1 || xx > n || yy < 1 || yy > m) continue;
    		if (a[xx][yy] != a[x][y] + 1) continue;
     
    		cnt++;
    		if (!vis[xx][yy]) dfs(xx, yy);
    		ans[x][y][1] = (ans[x][y][1] + ans[xx][yy][0]) % mod;
    		ans[x][y][2] = (ans[x][y][2] + ans[xx][yy][1]) % mod;
    		ans[x][y][3] = (ans[x][y][3] + ans[xx][yy][2] + ans[xx][yy][3]) % mod;
    	}
    	if (!cnt) ans[x][y][0] = 1;
    }
     
    signed main() {
    	scanf("%d%d", &n, &m);
    	rep(i,1,n + 1) rep(j, 1, m + 1) scanf("%d", &a[i][j]);
     
    	rep(i,1,n + 1) rep(j, 1, m + 1) if (!vis[i][j]) 
    		dfs(i, j);
     
    	i64 res = 0;
    	rep(i,1,n + 1) rep(j,1,m + 1) {
    		bool f = false;
    		rep(k, 0, 4) {
    			int xx = i + dx[k], yy = j + dy[k];
    			if (xx < 1 || xx > n || yy < 1 || yy > m) continue;
    			if (a[xx][yy] == a[i][j] - 1) {
    				f = true;
    				break;
    			}
    		}
    		if (!f) res = (res + ans[i][j][3]) % mod;
    	}
     
    	printf("%lld\n", (res + mod) % mod);
     
    	return 0 ^ 0;
    }

K

题目大意：给一个三角形，和一个端点，要我们在三角形的边上找到另一个点，是的两点所连的线段使这个三角形的面积被平分

解题思路：

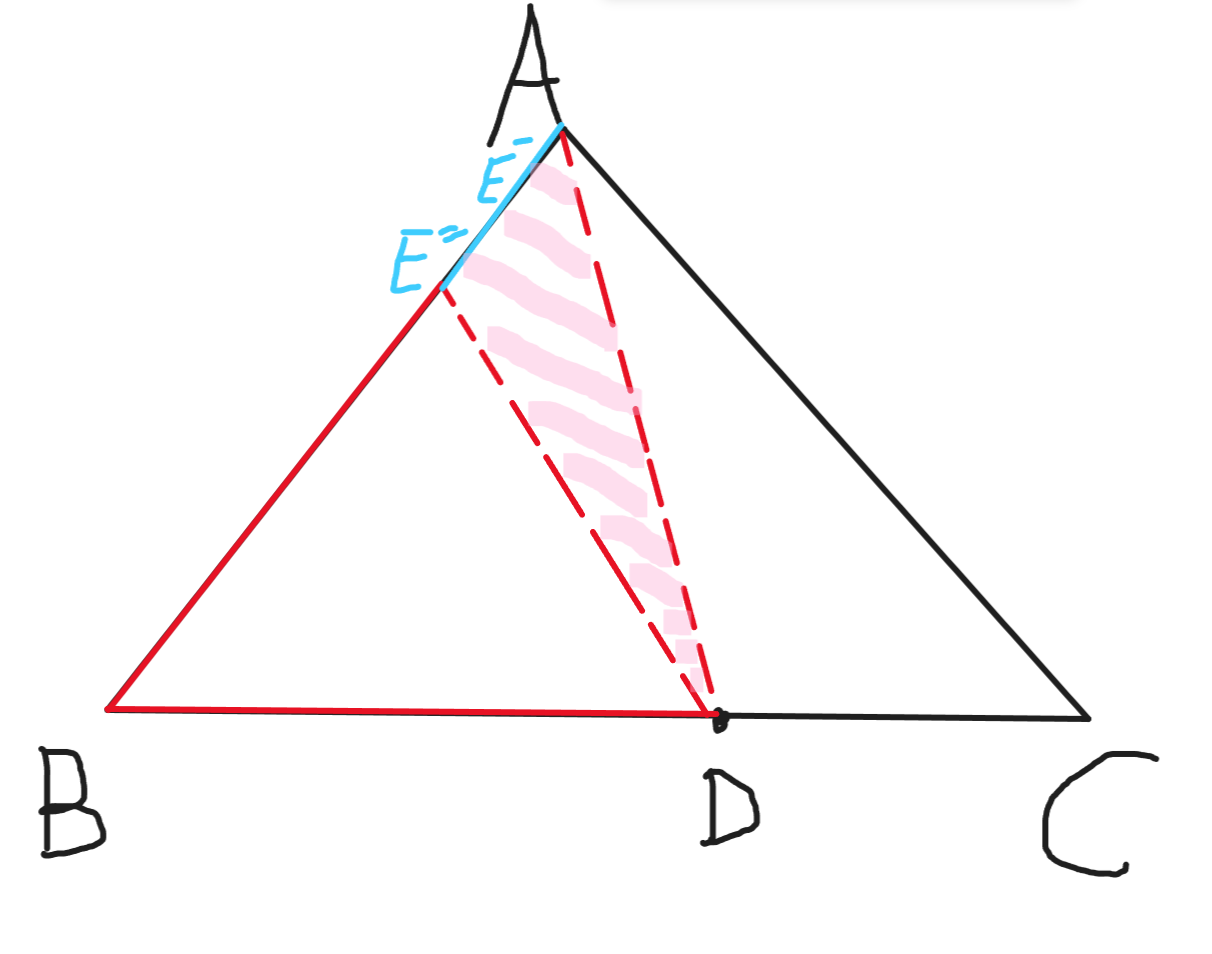
  移动\(E\)点使得\(S_\triangle {BDE} = \frac{1}{2} × S_\triangle{ABC}\)，而且由于三角形高相同，所以他们的面积之比就等于它们的底的比，就可以求出\(S_\triangle {ABD}\)和\(S_\triangle {BDE}\)之间的比例然后快速求出\(E\)的坐标。

代码：

点击查看代码

    constexpr double eps = 1E-7;
     
    int sgn(double x){
    	if(std::fabs(x) < eps) return 0;
        return x < 0 ? -1 : 1;
    }
     
    struct Point{
    	double x,y;
    	Point(){}
    	Point(double _x,double _y){
    		x = _x; y = _y;
    	}
    	Point operator -(const Point &b)const{
    		return Point(x-b.x,y-b.y);
    	}
    	double operator ^(const Point &b)const{
    		return x*b.y - y*b.x;
    	}
    	double operator *(const Point &b)const{
    		return x*b.x + y*b.y;
    	}
    };
     
    struct Line{
    	Point s,e;
    	Line(){}
    	Line(Point _s,Point _e){
    		s = _s; e = _e;
    	}
    	bool pointonseg(Point p){
    		return sgn((p - s) ^ (e - s)) == 0 && sgn((p - s) * (p - e)) <= 0;
    	}
    };
     
    double getS(Point a, Point b, Point c) { // 求面积
        Point vec1 = a-b;
        Point vec2 = a-c;
        return std::fabs(vec1^vec2)/2;
    }
     
    void getans(double S, Point a, Point b, Point c) {
        double d = S / getS(a, b, c);
        double dx = c.x - b.x, dy = c.y - b.y;
    	printf("%.7lf %.7lf\n", c.x - (1 - d) * dx, c.y - (1 - d) * dy);
    }
     
    void solve() {
    	Point p[3], pp;
    	for (int i = 0; i < 3; i++) scanf("%lf%lf", &p[i].x, &p[i].y);//std::cin >> p[i].x >> p[i].y;
    	scanf("%lf%lf", &pp.x, &pp.y);
    	Line L[3];
    	L[0] = {p[0], p[1]};
    	L[1] = {p[1], p[2]};
    	L[2] = {p[0], p[2]};
    	double res = getS(p[0], p[1], p[2]) / 2;
     
    	if (L[0].pointonseg(pp)) { // 0 1
    		if (sgn(getS(pp, p[1], p[2]) - res) >= 0) {
    			getans(res, pp, p[1], p[2]);
    		} else if (sgn(getS(pp, p[0], p[2]) - res) >= 0) {
    			getans(res, pp, p[0], p[2]);
    		} else {
    			printf("-1\n");
    		}
    	} else if (L[1].pointonseg(pp)) { // 1 2
    		if (sgn(getS(pp, p[0], p[2]) - res) >= 0) {
    			getans(res, pp, p[2], p[0]);
    		} else if (sgn(getS(pp, p[0], p[1]) - res) >= 0) {
    			getans(res, pp, p[1], p[0]);
    		} else {
    			puts("-1");
    		}
    	} else if (L[2].pointonseg(pp)) { // 0 2
    		if (sgn(getS(pp, p[1], p[2]) - res) >= 0) {
    			getans(res, pp, p[2], p[1]);
    		} else if (sgn(getS(pp, p[0], p[1]) - res) >= 0) {
    			getans(res, pp, p[0], p[1]);
    		} else {
    			puts("-1");
    		}
    	} else {
    		puts("-1");
    	}
    }