Codeforces Round #663 C. Cyclic Permutations(组合计数)

C. Cyclic Permutations

题意：
  给定一个\(n\)个数的排列，在\(1\sim n\)之间的选定一个位置，从这个位置向左向右分别找到第一个满足\(p_k \> p_i\)和\(p_j \> p_i\)且\(k \< i \< j\)，将\(i\)位置分别和\(j, k\)位置的点连一个无向边，使它们构成一个环。最后让我们求出\(n\)个数的全排列中一共能构成多少个环。
思路：
  这个题目的能构成环的情况有很多，比较难以计算，所以我们在这种情况下会选择正难则反的解决思路。先去考虑有哪些情况无法构成环，用总共的数量减去就可以很轻松的求解出来了。
因为我们要找到中间连边的点是要比左右的点高度低的，所以我们可以把这个排列抽象到二维平面中。例如样例中的\([4, 2, 1, 3]\)可以在二维平面中表示成

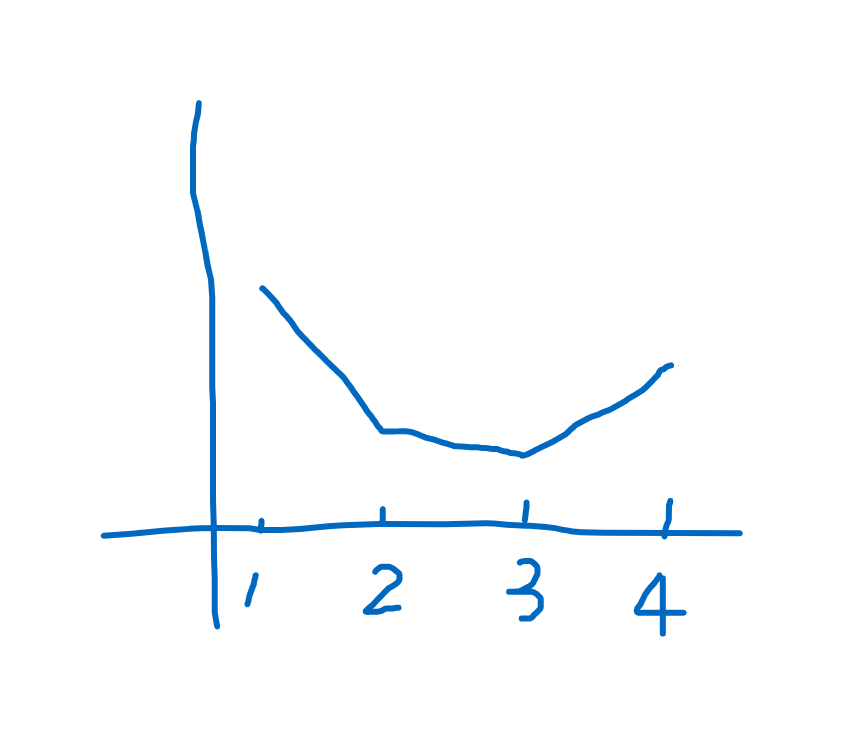
那么可以发现只要出现了\(\searrow \nearrow\)这样的话就可以满足题意连成一个环，所以我们只要保证排列中只会出现\(\nearrow \searrow\)这样的就可以了。那么我们将\(\max\limits_{1\leq i \leq n}{p_i}\)从最左边移动到最右边，在它的两侧所有元素单增单减即可，那么我们就得到了不能构成环的排列数是$$(\frac{n}{0}) + (\frac{n}{1}) + \dots + (\frac{n}{n- 1}) = 2^{n- 1}$$
总共的排列数就是\(A^{n}_{n} = n!\)，所以最终答案就是$$ans = n! - 2^{n- 1}$$

int n; std::cin >> n;
i64 ans = 1, res = 1;
for (int i = 1; i <= n; i ++ ) ans = 1ll * ans * i % P;
for (int i = 1; i <= n - 1; i ++ ) res = 2ll * res % P;
std::cout << (ans - res + P) % P << "\n";