【论文阅读】Attention Guided Graph Convolutional Networks for Relation Extraction[ACL2019]
论文地址:https://www.aclweb.org/anthology/P19-1024/
代码地址(Pytorch):https://github.com/Cartus/AGGCN
视频简介:https://www.youtube.com/watch?v=Mlh03htC1XY
Abstract
依赖树传递了丰富的结构信息,这些信息在文本实体之间的关系抽取任务上已经被证明有用。然而,如何有效地利用依赖树中的相关信息,同时忽略不相关信息仍然是一个挑战。现有的方法使用基于规则的硬剪枝策略来选择相关的部分依赖结构,可能并不总能得到最佳结果。本研究中,我们提出了 Attention Guided Graph Convolutional Networks (AGGCNs) ,能够直接将完全依赖树作为依赖树。我们的模型可以理解成一种软剪枝方法,可以自动地学习如何选择地关注相关的有用的子结构用于关系抽取任务。
现有的关系抽取模型可以分为两类:基于序列的 (sequence-based) 和基于依赖的 (dependency-based) 。基于序列的模型直接在词序列上进行操作,而基于依赖的模型将依赖树融合到模型中。与基于序列的模型相比,基于依赖关系的模型能够捕获从表面形式模糊的非局部句法关系。
基于规则的剪枝策略可能会丢失整个树中的一些重要信息。Figure 1 显示了跨句子 nnn 元关系抽取中的一个示例,如果模型仅考虑修剪的树,则将排除关键 token 的部分响应。
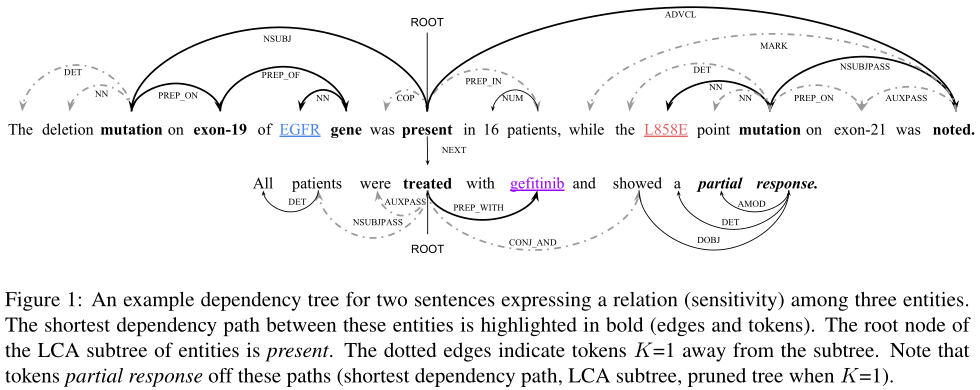
理想情况下,模型应该能够学习如何在包含和排除完整树中的信息之间保持平衡。在本文中,我们提出了新型 Attention Guided Graph Convolutional Networks (AGGCNs) ,直接在整棵树上操作。直观地说,我们开发了一种“软修剪”策略,将原始依赖树转换为完全连通的边加权图。这些权重可以看作是节点之间的关联强度,可以通过自注意机制进行端到端的学习。
为了对一个大的全连接图进行编码,我们在 GCN 模型中引入了 dense connections。对于GCNs,需要 LLL 层来捕获 LLL 跳距离的领域信息。浅层的 GCN 模型不能捕获大图的非局部交互。有趣的是,虽然较深的gcn可以捕捉到更丰富的图的邻域信息,但从经验上看,两层模型的性能最好。 在 dense connections 的帮助下,我们能够对AGGCN模型进行大的深度训练,从而能够捕获丰富的局部和非局部依赖信息。
我们的贡献总结如下:•我们提出了一种新的AGGCNs,它以端到端的方式学习“软剪枝”策略,学习如何选择和丢弃信息。结合稠密连接,我们的AGGCN模型能够学习更好的图表示。•与以前的GCN相比,我们的模型在没有额外计算开销的情况下获得了最新的结果【表示完全连通图的邻接矩阵的大小与原树的邻接矩阵的大小相同。】。与树结构模型(例如TreeLSTM(Tai et al,2015))不同,它可以有效地并行应用于依赖树。
2 Attention Guided GCNs
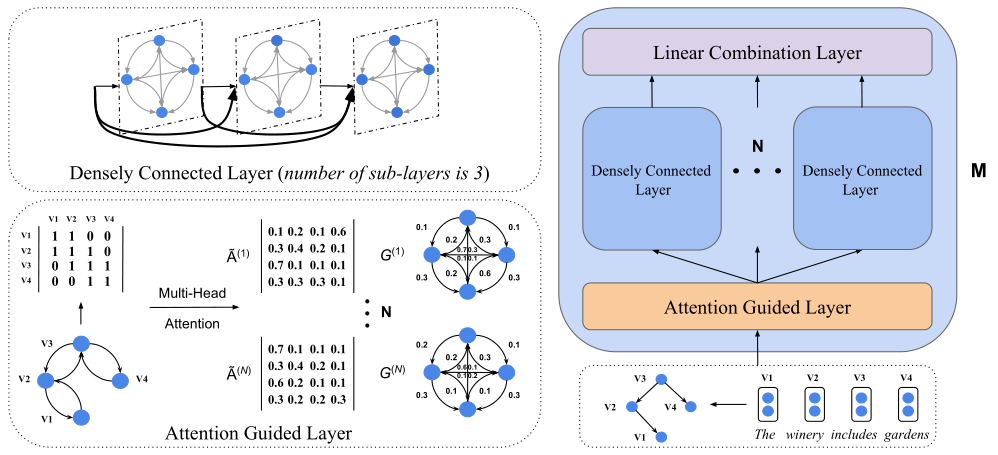
图2:AGGCN模型显示了一个示例语句及其依赖树。它由M个相同的块组成,每个块有三种类型的层,如右图所示。每个块都以节点嵌入和表示图的邻接矩阵作为输入。然后利用左下角所示的多头注意构造N个注意引导的邻接矩阵。将原依赖树转化为N个不同的全连通边加权图(为了简化,省略了自循环)。边缘附近的数字表示矩阵中的权重。生成的矩阵被送入N个独立的密集连接层,生成新的表示。左上角显示了密集连接层的示例,其中子层的数量(L)为3(L是一个超参数)。每个子层连接所有前面的输出作为输入。最后,应用线性组合将N个密集连接层的输出组合成隐藏表示。
2.1 GCNs
GCNs是可以直接在图结构上进行操作的神经网络。这里我们通过数学形式来阐述多层的GCNs 如何在图上work。给定一个具有 $n$ 个节点的图,我们可以用一个 $n \times n$ 的邻接矩阵 $A$ 来表示这个图。Marcheggiani and Titov (2017) 通过将边的方向性融合到模型中来编码依赖树,从而扩展了GCNs。他们对树中的每个节点增加了一个自环。如果一条边连接了节点 $i$ 到节点 $j$ ,则 $A_{ij}=1$ 并且 $A_{ji}=1$ ,否则 $A_{ij}=0$ 并且 $A_{ji}=0$ 。节点 $i$ 在第 $l$ 层的卷积计算将 $h^{l-1}$ 作为输入,输出 $h_i^{(l-1)}$ ,可以定义为:
$h_i^{(l)}=\rho (\sum_{j=1}^nA_{ij}W^{(l)}h_j^{(l-1)}+b^{(l)})$
$W^{(l)}$ 是权重矩阵,$\rho$ 是一个激活函数(例如 RELU),$h_i^{(0)}$ 是初始的输入 $\text{x}_i$ ,$\text{x}_i \in \mathbb{R}^d$ ,$d$ 是输入特征的维度。
2.2 Attention Guided Layer
AGGCN模型由 $M$ 个独立的模块组成。每个模块由三种类型的层组成:attention guided layer,densely connected layer 和 linear combination layer。
大多数现有的剪枝策略是与定义的,它们将完整的树剪成一个子树,基于此构建了邻接矩阵。事实上,这样的策略也可以被视为 hard attention 的一种形式。这样的策略可能丢失原始依赖树中的相关信息。而我们在 attention guide layer 上开发了一种“软剪枝”策略,可以为所有的边分配权重。这些权重可以通过模型以端到端的形式来学习。
在 attention guide layer ,我们通过构造一个 attention guided 邻接矩阵 $\tilde{A}$ 将原始的依赖树转换成一个全连接的加权边的图。每个 $\tilde{A}$ 对应一个具体的全连接图,并且每个 $\tilde{A_{ij}}$ 是从节点 $i$ 到节点 $j$ 的边权重。$\tilde{A}^{(1)}$ 表示一个全连接图 $G^{(1)}$ 。$\tilde{A}$ 可以通过 self-attention mechansim 来构造。一旦我们得到了 $\tilde{A}$ ,我们可以使用它作为计算 GCN 层的输入。 注意,$\tilde{A}$ 的 size 与原始的邻接矩阵 $A(n \times n)$ 一样。因此没有额外的计算开销。Attention guided layer 的关键想法是使用注意力用于引入节点之间的关系,特别是对于那些间接的、多跳的连接。这些 soft relations 可以通过模型中的可导函数来捕获。
我们通过使用 multi-head attention 来计算 $\tilde{A}$ 。计算包含了一个 query 和一组 key-value pairs。输出被计算为 values 的加权和,权重通过一个函数来计算:
$\tilde{A}^{(t)} = softmax(\frac{QW_i^Q \times (KW_i^K)^T}{\sqrt{d}})V$
其中 $Q$ 和 $K$ 都等于在 $l-1$ 层的集合表示 (collective representation) $h^{(l-1)}$。$\tilde{A}^{(t)}$ 是第 $t$ 个 attention guided 邻接矩阵,对应于第 $t$ 个head。构造了多达 $N$ 个矩阵,其中 $N$ 是超参数。在实际中,我们将原始邻接矩阵视为初始化,以便在节点表示中捕捉依赖信息,用于后面进行注意力计算。从第二块中开始包含 attention guided layer 。
2.3 Densely Connected Layer
与以前的修剪策略不同,它们导致生成的结构比原始结构小,而我们的 attention guided layer 会输出较大的完全连接图。另外,我们引入了 dense connections ,用于在大图中捕获更多的结构信息。在 dense connections 的帮助下,我们能够训练更深的模型,从而可以捕获丰富的局部和非局部信息,以学习更好的图表示。
Dense connectivity 如模型图所示,任意层都能直接与之前层连接。我们首先将 $g_j^{(l)}$ 定义为初始节点表示与产生于 $1,...,l-1$ 层的节点表示的拼接。
$g_j^{(l)} = [x_j;h_j^{(1)};...;h_j^{(l-1)}]$
实际中,每个 dense connected layer 有 $L$ 个子层。这些子层的的维度 $d_{hidden}$ 被 $L$ 和输入特征维度 $d$ 决定。在 AGGCNs 中,我们使用 $d_{hidden}=d/L$ 。例如,如果 densely connected layer 有 3 个子层,并且输入维度为 300 ,则每个子层的隐藏维度为 $d_{hidden}=d/L=300/3=100$ 。然后我们将每个子层的输出进行拼接,形成一个新的表示。因此,输出的维度是 300 ($3 \times 100$) 。不同于 GCN 模型,它的隐藏维度大于或等于输入维度,而 AGGCN 模型随着层数的增加而缩小隐藏维度,以提高参数效率。
由于我们有 $N$ 个不同的 attention guided 邻接矩阵,需要 $N$ 个独立的 densely connected layers。因此,我们修改每层的计算如下(对于第 $t$ 个矩阵 $\tilde{A}^{(t)}$):
$h_{t_i}^{(l)} = \rho (\sum_{j=1}^n \tilde{A}_{ij}^{(t)} W_t^{(l)} \mathbb{g}_j^{(l)} + b_t^{(l)})$
$W^{(l)}_t ∈ R^{d_{hidden}×d(l)}$, where $d(l)= d + d_{hidden}× (l − 1)$.
2.4 Linear Combination Layer
线性连接层用于去融合 $N$ 个不同的 densely connected layers 。
$h_{comb} = W_{comb}h_{out} + b_{comb}$
$h_{out}$ 是是将 $N$ 个 densely connected layers 的输出拼接而成的,$h_{out}=[h^{(1)};...;h^{(N)}] \in \mathbb{R}^{d \times N}$ 。
2.5 AGGCNs for Relation Extraction
将 AGGCN 应用到依赖树之后,我们得到所有 tokens 的隐藏表示。根据这些表示,关系抽取的目标是要预测实体之间的关系。我们将句子表示和实体表示拼接来得到用于分类的最终表示。首先,我们需要得到句子表示 $h_{sent}$ 。它可以计算为:
$h_{sent} = f(h_{mask}) = f(AGGCN(\text{x}))$
$h_{mask}$ 表示 masked collective hidden representations。这里的 masked 意思是我们仅选择那些不是 entity tokens 的 tokens 的表示。$f:\mathbb{R}^{d \times n} \rightarrow \mathbb{R}^{d \times 1}$ 是一个 max pooling function ,将 $n$ 个输入向量映射到 1 个句子向量。类似地,我们可以得到实体表示。对于第 $i$ 个实体,它的表示 $h_{e_i}$ 可以被计算为:
$h_{e_i} = f(\text{h}_{e_i})$
$\text{h}_{e_i}$ 表示第 $i$ 个实体的隐藏表示。实体表示与句子表示拼接形成一个新的表示。再应用一个前馈神经网络:
$h_{final} = \text{FFNN}([h_{sent};h_{e_1};...h_{e_i}])$
3 Experiments
3.1 Data
我们评估了我们的模型在两个任务上的性能,即跨句n元关系抽取和句子级关系抽取。对于跨句n元关系提取任务,我们使用(Peng et al.,2017)中介绍的数据集,其中包含6987个三元关系实例和6087个从PubMed中提取的二元关系实例。5大多数实例包含多个句子,每个实例都分配有五个标签中的一个,包括“抵抗或无反应”、“敏感”、“反应”、“抵抗”和“无”“resistance or nonresponse”, “sensitivity”, “response”, “resistance” and “none”。我们考虑两个具体的评估任务,即二类n元关系抽取和多类n元关系抽取。对于二元类n元关系提取,我们遵循(Peng et al.,2017)将四个关系类分组为“是”,并将“无”视为“否”通过将四个关系类分组为“yes”并将“none”视为“no”,对多类标签进行二值化,从而对多类标签进行二值化
对于句子级关系提取任务,我们遵循(Zhang et al.,2018)中的实验设置,在TACRED数据集(Zhang et al.,2017)和Semeval-10任务8(Hendrickx et al.,2010)上评估我们的模型。TACRED数据集有超过106K个实例,它引入了41种关系类型和一种特殊的“无关系”类型来描述实例中提及对之间的关系。Subject mentions分为“个人”和“组织”,而Object mentions分为16种细粒度类型,包括“日期”、“地点”等。Semeval-10任务8是一个公共数据集,包含10717个实例,其中包含9个关系和一个特殊的“其他”类。
3.2 Setup
- n-ary
- 与(Song et al., 2018b)4相同的数据分割
- 句子级
- (Zhang et al., 2018)相同的开发集
- embedding:840B-300d-glove
- 超参数
- N(attention head数目)
- {1,2,3,4}
- L(densely connected中每层的维度)
- {2,3,4,5,6}
- M(块数)
- {1,2,3}
- N(attention head数目)
- 测试得到最好的超参数:
- cross-sentence n-ary
- {N=2,M=2,L=5,d_{hidden}=340}
- {N=3,M=2,L=5,d_{hidden}=300}
- cross-sentence n-ary
- 度量
- 和(Song et al., 2018b; Zhang et al., 2018).一样
- n-ary
- test:5-fold cross validation
- 句子
- micro-F1 score
- TACRED
- SemEval (macro-F1 score)
- micro-F1 score
3.3 Results on Cross-Sentence n-ary Relation Extraction
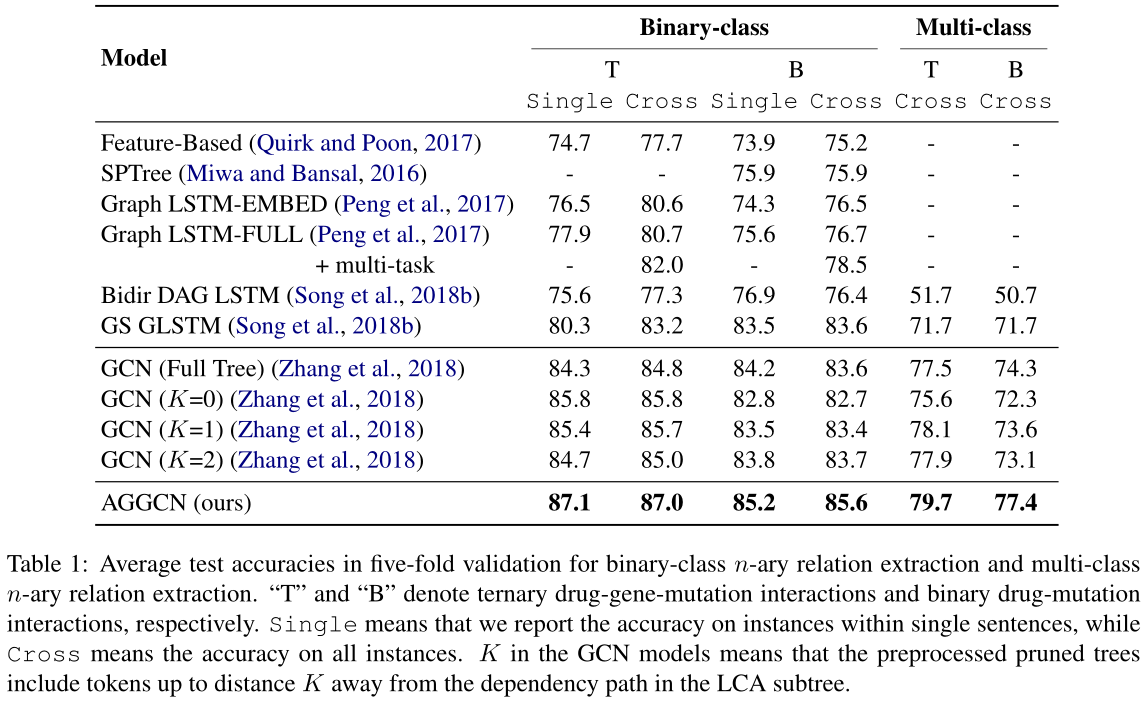
表1:二类n元关系提取和多类n元关系提取的五倍验证平均测试精度。“T”和“B”分别表示三元药物-基因突变相互作用和二元药物-基因突变相互作用。“单一”是指我们报告单个句子中实例的准确性,而“交叉”是指所有实例的准确性。GCN模型中的K表示经过预处理的剪枝树中包含了距离LCA子树中依赖路径K的标记。
这些结果表明,与以前基于全树的方法(如GS-GLSTM)相比,AGGCN能够从底层的图结构中提取更多的信息,通过图卷积学习更具表现力的表示。AGGCN的性能也优于GCNs,尽管它的性能可以通过修剪树来提高。我们认为这是由于密集连接层和注意引导层的结合。密集连接可以促进大型图中的信息传播,使AGGCN能够有效地从长距离依赖中学习,而无需剪枝技术。同时,注意引导层可以进一步从密接层学习到的表示中提取相关信息并滤除噪声。
对于三元和二元关系,我们的AGGCN模型仍然比GS-GLSTM模型分别高8.0和5.7个点。我们还注意到,我们的AGGCN比所有GCN模型具有更好的测试精度,这进一步证明了它能够从全树中学习更好的表示。
3.4 Results on Sentence-level Relation Extraction
现在,我们在TACRED数据集上报告表2中句子级关系提取任务的结果。我们将我们的模型与两种模型进行了比较:1)基于依赖的模型,2)基于序列的模型。基于依赖关系的模型包括逻辑回归分类器(LR)(Zhang et al.,2017)、最短路径LSTM(SDPLSTM)(Xu et al.,2015c)、树结构神经模型(Tree LSTM)(Tai et al.,2015)、GCN和情境化GCN(C-GCN)(Zhang et al.,2018)。GCN和C-GCN模型都使用修剪过的树。对于基于序列的模型,我们考虑了最先进的位置感知LSTM(PA-LSTM)(Zhang等人,2017)。
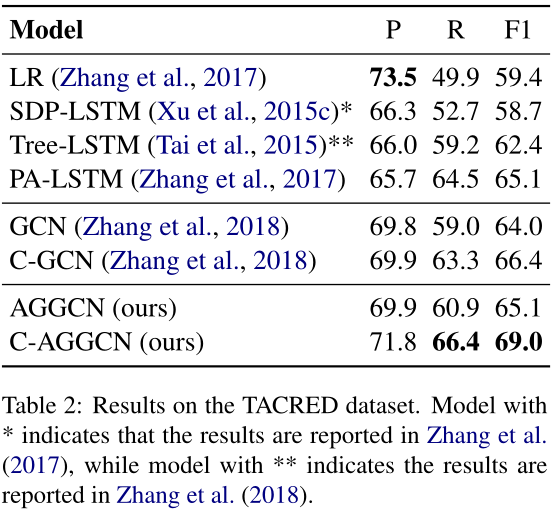
如表2所示,logistic回归分类器(LR)获得了最高的精度分数。我们假设,这背后的原因是由于数据不平衡的问题。这种基于特征的方法倾向于预测一个高度频繁的标签作为关系(例如per:标题”). 因此,它具有较高的精度,同时具有相对较低的召回率。另一方面,神经网络模型能够更好地平衡查准率和查全率。
由于GCN和C-GCN已经显示出了它们相对于其他依赖模型和PA-LSTM的优越性,我们主要将我们的AGGCN模型与它们进行了比较。我们可以观察到AGGCN比GCN高出1.1个F1点。我们推测,有限的改善是由于缺乏语境信息的语序或消歧。与C-GCN(Zhang et al.,2018)类似,我们使用双向LSTM网络扩展了AGGCN模型,以捕获随后输入AGGCN层的上下文表示。我们将修正后的模型称为C-AGGCN。我们的C-AGGCN模型的F1得分为69.0,比现有的C-GCN模型高出2.6分。我们还注意到,AGGCN和C-AGGCN分别比GCN和C-GCN获得更好的查准率和查全率。实验结果表明,基于剪枝树的GCNs模型和基于全树的AGGCNs模型在区分相关信息和无关信息方面有较好的性能。
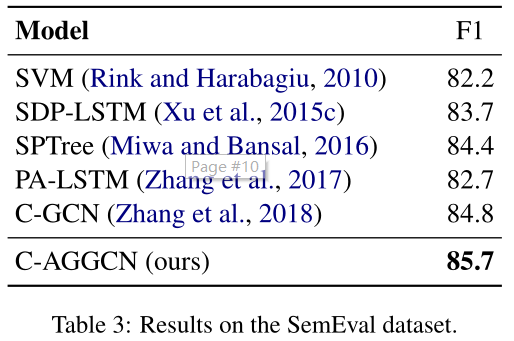
我们还在SemEval数据集上评估了我们的模型,设置与(Zhang等人,2018年)相同。结果见表3。这个数据集比TACRED小得多(就实例数量而言,只有TACRED的1/10)。我们的C-AGGCN模型(85.7)始终优于C-GCN模型(84.8),显示出良好的可推广性。
3.5 Analysis and Discussion
Ablation Study
我们使用TACRED数据集上表现最好的C-AGGCN模型来检验两个主要组成部分,即密集连接层和注意引导层的贡献。表4显示了结果。我们可以观察到,添加注意引导层或密集连接层都可以提高模型的性能。这表明,这两个层次都可以帮助GCNs学习更好的信息聚合,产生更好的图形表示,其中注意力引导层似乎扮演着更重要的角色。我们还注意到前馈层在我们的模型中是有效的。如果没有前馈层,结果会下降到F1的67.8分。

Performance with Pruned Trees.
表5显示了具有修剪树的C-AGGCN模型的性能,其中K表示修剪树包括距离LCA子树中的依赖路径K的令牌。我们可以观察到,所有具有不同K值的C-AGGCN模型都能够优于最先进的C-GCN模型(Zhang等人,2018)(见表2)。具体来说,在K=1的相同设置下,C-AGGCN超过C-GCN 1.5分的F1分数。这表明,在密集连接层和注意引导层的结合下,对于下游任务,C-AGGCN比C-GCN能更好地学习图的表示。此外,我们注意到,具有完整树的C-AGGCN的性能优于所有具有修剪树的C-AGGCN。这些结果进一步说明了“软剪枝”策略在利用全树信息方面优于硬剪枝策略。

Performance against Sentence Length
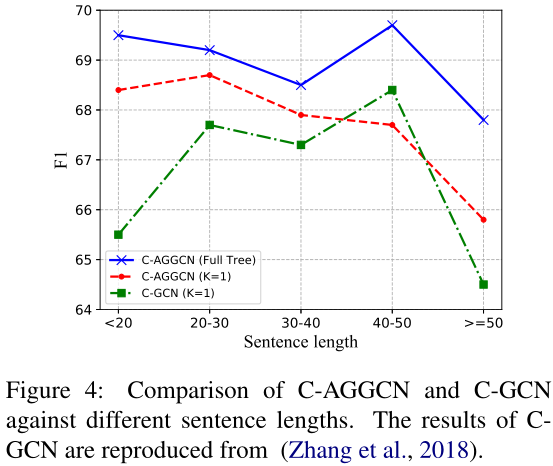
图4显示了三个模型在不同句子长度下的F1分数。我们将句子长度分成五类(<20,[20,30],[30,40],[40,50],≥50)。总的来说,对于不同的句子长度,带全树的C-AGGCN要优于带修剪树的C-AGGCN和C-GCN。我们还注意到,在大多数情况下,带修剪树的C-AGGCN比C-GCN性能更好。此外,C-AGGCN对剪枝树的改进效果随着句子长度的增加而衰减。这种性能下降可以通过使用完整树来避免,它提供了底层图结构的更多信息。直观地说,随着句子长度的增加,依赖图随着节点的增加而变大。这表明C-AGGCN可以从更大的图(全树)中获益更多。
Performance against Training Data Size.
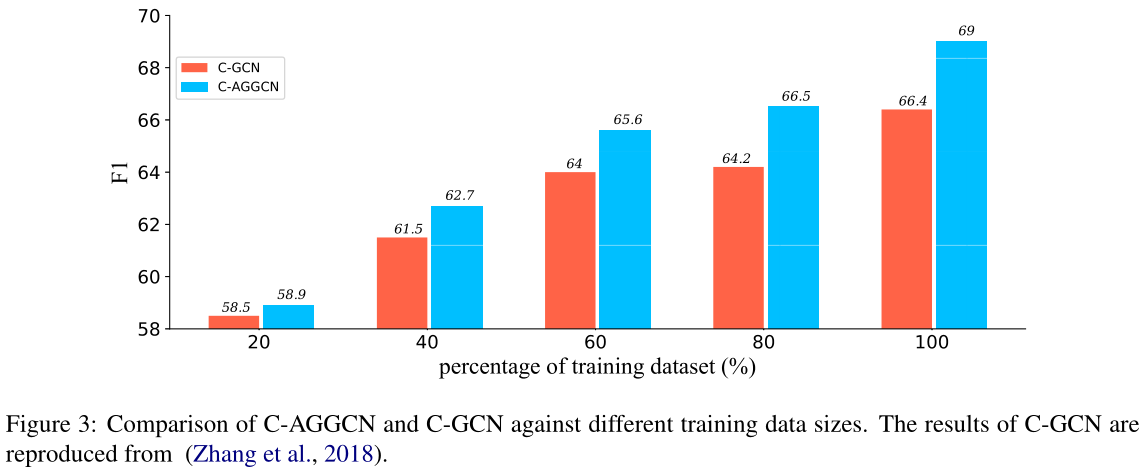
图3显示了C-AGGCN和C-GCN在不同训练设置下的性能,训练数据量不同。我们考虑五种训练设置(20%、40%、60%、80%、100%的训练数据)。在相同的训练数据量下,C-AGGCN始终优于C-GCN。当训练数据的大小增加时,我们可以观察到性能差距变得更加明显。具体来说,使用80%的训练数据,C-AGGCN模型能够获得66.5的F1分数,高于在完整训练集上训练的C-GCN。这些结果表明,我们的模型更有效地利用了培训资源。
5 Conclusion
介绍了一种新颖的注意引导图卷积网络(AGGCNs)。实验结果表明,AGGCNs在各种关系抽取任务上都取得了很好的效果。与以前的方法不同,AGGCNs直接在完整的树上操作,并学习以端到端的方式从中提取有用的信息。未来的工作有多个场所。我们想问的一个自然问题是,如何利用提出的框架对图形相关任务执行改进的图形表示学习(Bastings et al.,2017)。
参考:
Chenhao's Studio:http://chenhao.space/post/27e4eea7.html#aggcns-for-relation-extraction
叶落叶子:https://blog.csdn.net/weixin_40485502/article/details/104281275



 浙公网安备 33010602011771号
浙公网安备 33010602011771号