差分约束系统的相关事宜
差分约束系统针对于将不等式方程组转化为图论中最短路或者最长路问题,可以看做是各种问题与图论之间相互联系的桥梁。
比如在此图中求解x3-x0的最大值,就相当于求x0->x3的最短路,形如a-b<=c的式子可以转化为a<=c+b-->dis[a]<=w(a,b)+dis[b]这样类似于最短路或最长路的表达式。
用这些不等式建边的注意事项:
- 不等式一定是减式(因为是【差分】约束)。
- 在减数->被减数间存在一条权值为右侧常数的边。
- 根据不等号方向确定是求最短路还是最长路。一般大于号是求最长路(求最小值),小于号是求最短路(求最大值)。
- 如果方程组内存在不等号方向不一致的情况,需要选择一些式子进行变号直至符号相同。
解的存在性:
- 如果终点值是预设值,那么说明终点无法到达,无解
- 如果存在负环且要求求出最短路,那么也无解(spfa判断,负环成立条件是某点入队次数>sqrt(总点数))。
- 其余情况一般有解


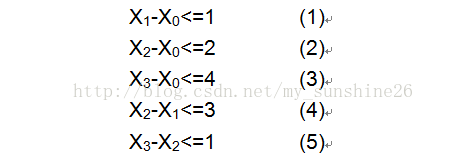

 浙公网安备 33010602011771号
浙公网安备 33010602011771号