QOJ7221

常规题，如果会北京集训 D1T3，那这题就是砍瓜切菜。

首先注意到如果边没有任何性质的话大概率是个不可做（可能是 NP 但是我不了解）

那肯定就要从边的性质来做这题。

画个图来感受一下：

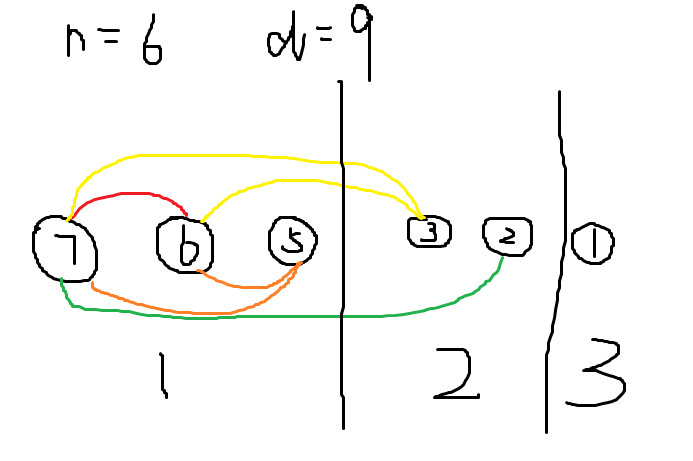
按照边权从大到小排序，连边。可以将点集划分为三部分：

第一部分两两点之间都有边，也就是个团。第二部分的每个点只会向第一部分的每个点连一条边。第三部分是孤立点。

首先孤立点的贡献是简单的，每个点染什么颜色都不会影响答案。

注意到第二部分的点都是向一个第一部分的前缀连边，我们不妨在这个前缀的末尾算贡献。

现在就可以动态规划了，设 \(f_{i,j}\) 表示前 \(i\) 个点有 \(j\) 个白点，贡献（边两边颜色不同）最大是多少。

那么从大到小枚举第一部分的点。

那么加入第一部分的点：\(f_{i,j}=max(f_{i-1,j-1}+i-j,f_{i-1,j}+j)\)。

加入第二部分的点：\(f_{i,j}=f_{i,j}+max(i-j,j)\)。

题目说还有求方案数，再设 \(g_{i,j}\) 表示前 \(i\) 个点有 \(j\) 个白点取到最大值的时候的方案数。

当 \(f\) 的更新的时候 \(g\) 顺便维护一下即可。

复杂度 \(O(n^2)\)。

应该比题解好想好写。

#include<bits/stdc++.h>
using namespace std;

typedef long long ll;
const ll N=1e4+3,H=998244353;
ll n,d,a[N],cnt[N],f[N],laf[N],g[N],lag[N];
int main()
{
	cin>>n>>d;ll sx=1;
	for(int i=1;i<=n;i++)cin>>a[i];
	sort(a+1,a+n+1,[&](int x,int y){return x>y;});
	int k=0;memset(f,-0x3f,sizeof(f));f[0]=0;g[0]=1;
	for(int i=1;i<=n;i++)if(a[i]*2>=d)k=i;
	for(int i=1,j=n;j>k;j--)
	{
		while(i<k&&a[i+1]+a[j]>=d)i++;
		if(i<=k&&a[i]+a[j]>=d)cnt[i]++;
		else sx=sx*2%H; 
	}
	for(int i=1;i<=k;i++)
	{
		swap(f,laf);swap(g,lag);
		memset(f,-0x3f,sizeof(f));memset(g,0,sizeof(g)); 
		f[0]=laf[0];g[0]=lag[0];f[i]=laf[i-1];g[i]=lag[i-1];
		for(int j=1;j<i;j++)
		{
			f[j]=max(laf[j-1]+i-j,laf[j]+j);
			g[j]=((laf[j-1]+i-j==f[j])*lag[j-1]+(laf[j]+j==f[j])*lag[j])%H;
		}
		for(int p=1;p<=cnt[i];p++)for(int j=0;j<=i;j++)
			f[j]+=max(j,i-j),g[j]=g[j]*(1+(j==i-j))%H;
	}
	ll mx=0,ans=0;
	for(int j=0;j<=k;j++)mx=max(mx,f[j]);
	for(int j=0;j<=k;j++)if(f[j]==mx)ans=(ans+g[j])%H;
	cout<<mx<<" "<<ans*sx%H;
}