Codeforces Global Round 1

A

 

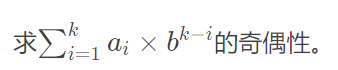
 题解：倒叙枚举即可。

#include<bits/stdc++.h>
using namespace std;
 
typedef long long ll;
const ll N=1e6+3;
ll b,k,a[N];
void Solve()
{
    cin>>b>>k;ll s=0,p=1;
    for(int i=1;i<=k;i++)cin>>a[i];
    for(int i=k;i>0;i--)s=(s+p*a[i])%2,p=p*b%2;
    if(s%2==0)cout<<"even"<<endl;
    else cout<<"odd"<<endl;
}
int main()
{
    int T;T=1;
    while(T--)Solve();
}

 

 B

 

 

 题解：当没有 $k$ 的限制的时候，答案就为 $n$。考虑当 $k$ 逐渐减小的时候，就贪心覆盖的最近的两个点。

#include<bits/stdc++.h>
using namespace std;
 
typedef long long ll;
const ll N=1e6+3;
ll n,m,k,a[N],b[N];
void Solve()
{
    cin>>n>>m>>k;ll s=n;
    for(int i=1;i<=n;i++)cin>>a[i];
    for(int i=1;i<n;i++)b[i]=a[i+1]-a[i]-1;
    sort(b+1,b+n);
    for(int i=1;i<=n-k;i++)s+=b[i];
    cout<<s<<endl;
}
int main()
{
    int T;T=1;
    while(T--)Solve();
}

 

C

 

 

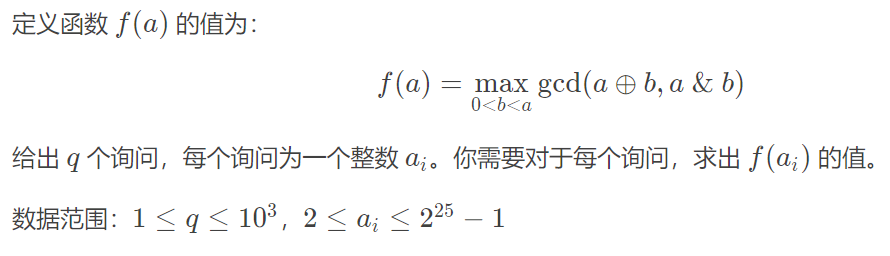
 题解：手玩几组数据后，发现除了  $2^n-1$ 这类数，其他所有数的答案都是 $2^{floor(log2(2))+1}-1$。

然后对于 $2^n-1$ 这类数，发现 $a^b=a-b，a&b=b$，那么 $f(a)=gcd(a-b,b)=gcd(a,b)$，也就是当 $b$ 是 $a$ 的最大因数时，答案最大，根号暴力即可。

#include<bits/stdc++.h>
using namespace std;
 
typedef long long ll;
const ll N=1e6+3;
ll n;
void Solve()
{
    cin>>n;ll k=64-__builtin_clzll(n),p=(1<<k)-1;
    if(p==n)
    {
        for(ll i=2;i*i<=n;i++)if(n%i==0){cout<<n/i<<endl;return;}
        cout<<1<<endl;
    }
    else cout<<(1<<k)-1<<endl;
}
int main()
{
    int T;cin>>T;
    while(T--)Solve();
}

 

D

 

 

 题解：妙妙dp题

科普：三个一样的牌叫刻子，三个连续的牌叫顺子。

显然，三组连续的刻子和三组一样的顺子是等价的。所以对于任意一种刻子最多只会使用两次。

于是考虑暴力dp设状态。就设 $fi,a,b$ 表示第 $i$ 个值选了 $a$ 个 $i-1,i,i+1$ , $b$ 个 $i,i+1,i+2$

然后再枚举个 $c$ 个 $i+1,i+2,i+3$，暴力转移即可。

#include<bits/stdc++.h>
using namespace std;
 
typedef long long ll;
const int N=1e6+3;
ll n,m,p[N],f[N][3][3];
void Solve()
{
    cin>>n>>m;
    for(int i=1,x;i<=n;i++)cin>>x,p[x]++;
    for(int i=0;i<=m;i++)for(int a=0;a<3;a++)for(int b=0;b<3;b++)for(int c=0;c<3;c++)if(p[i+1]>=a+b+c)
        f[i+1][b][c]=max(f[i+1][b][c],f[i][a][b]+c+(p[i+1]-a-b-c)/3);
    cout<<f[m][0][0]<<endl;
}
int main()
{
    int T;T=1;
    while(T--)Solve();
    return 0;
}

 

E

 

 题解：这题真的一眼……做过了NOIP2021的方差，这题真的像切菜一样。

首先显然，如果第一个位置和最后一个位置不一样的话肯定就不行。

然后就是你发现操作其实就是交换相邻两数的差分数组。判断一下俩数据的差分数组是否相同即可。

#include<bits/stdc++.h>
using namespace std;
 
typedef long long ll;
const ll N=1e6+3;
ll n,a[N],b[N],c[N],d[N];
void Solve()
{
    cin>>n;
    for(int i=1;i<=n;i++)cin>>a[i];
    for(int i=1;i<=n;i++)cin>>b[i];
    if(a[1]!=b[1]||a[n]!=b[n]){cout<<"No"<<endl;return;}
    for(int i=1;i<n;i++)c[i]=a[i+1]-a[i],d[i]=b[i+1]-b[i];
    sort(c+1,c+n);sort(d+1,d+n);
    for(int i=1;i<n;i++)if(c[i]!=d[i]){cout<<"No"<<endl;return;}
    cout<<"Yes"<<endl;
}
int main()
{
    int T;T=1;
    while(T--)Solve();
}

 

F

 

 不会，咕咕咕。

G

 

 不会，咕咕咕。

H

 

 不会，咕咕咕。