Codeforces Global Round 21

A 

 

 题解：$z$ 只会越来越小，成为一开始的 $z$ 的子集，所以 $a_i$ 能取到最大值时就是与一开始的 $z$ 进行一次操作。

#include<bits/stdc++.h>
using namespace std;
 
typedef long long ll;
const ll N=1e6+3,H=1e9+7;
ll n,x,a[N];
void Solve()
{
    cin>>n>>x;ll s=0;
    for(int i=1;i<=n;i++)cin>>a[i],s=max(s,a[i]|x);
    cout<<s<<endl;
}
int main()
{
    int T;cin>>T;
    while(T--)Solve();
}

B

 

 题解：显然答案只能为 $0,1,2$。将 $0,1$ 的情况排除，剩余输出 $2$。

答案为 $0$ 的时候显然就是全局为 $0$。

答案为 $1$ 的时候就是去掉前缀 $0$ 和后缀 $0$ 之后中间没有 $0$ 的情况。

#include<bits/stdc++.h>
using namespace std;
 
typedef long long ll;
const ll N=1e6+3,H=1e9+7;
ll n,a[N];
void Solve()
{
    cin>>n;ll x=0,y=0;
    for(int i=1;i<=n;i++)cin>>a[i],x+=a[i]==0;
    if(x==n){cout<<0<<endl;return;}
    ll px=0,py=0;
    for(int i=1;i<=n;i++)if(a[i]==0)px++;else break;
    for(int i=n;i>0;i--)if(a[i]==0)py++;else break;
    for(int i=px+1;i<=n-py;i++)if(a[i]==0){cout<<2<<endl;return;}
    cout<<1<<endl; 
}
int main()
{
    int T;cin>>T;
    while(T--)Solve();
}

C

 

 题解：显然 $a$ 能否变成 $b$ 等价于把 $a$ 全部分裂，$b$ 全部分裂后是否相等。

#include<bits/stdc++.h>
using namespace std;
 
typedef long long ll;
const ll N=1e6+3,H=1e9+7;
ll n,m,k,a[N][3],b[N][3];
void Solve()
{
    cin>>n>>m;
    for(int i=1;i<=n;i++)
    {
        cin>>a[i][0];a[i][1]=1;a[i][2]=a[i][0];
        while(a[i][2]%m==0)a[i][2]/=m,a[i][1]*=m;
    }
    cin>>k;
    for(int i=1;i<=k;i++)
    {
        cin>>b[i][0];b[i][1]=1;b[i][2]=b[i][0];
        while(b[i][2]%m==0)b[i][2]/=m,b[i][1]*=m;
    }
    int i=1,j=1;
    for(;i<=n&&j<=k;)
    {
        if(a[i][2]!=b[j][2]){cout<<"No"<<endl;return;}
        if(a[i][1]==b[j][1]){a[i][1]=b[j][1]=0;i++;j++;continue;}
        if(a[i][1]>b[j][1])a[i][1]-=b[j][1],b[j][1]=0,j++;
        else b[j][1]-=a[i][1],a[i][1]=0,i++;
    }
    if((i<=n&&a[i][1]>0)||(j<=k&&b[j][1]>0))cout<<"No"<<endl;
    else cout<<"Yes"<<endl; 
}
int main()
{
    int T;cin>>T;
    while(T--)Solve();
}

D

 

 题解：这题很妙妙。本题全为感性证明。

从一个点到另一个点肯定会经过区间内的最小值的点和最大值的点。（重点）

然后就可以预处理最大值最小值+分治答案

#include<bits/stdc++.h>
using namespace std;
 
typedef long long ll;
const int N=1e6+3,M=23;
ll n,a[N],ma[N][M],mb[N][M];
ll Ma(ll x,ll y){return a[x]>a[y]?x:y;}
ll Mb(ll x,ll y){return a[x]<a[y]?x:y;}
void Pre()
{
    for(int i=1;i<=n;i++)ma[i][0]=mb[i][0]=i;
    for(int j=1;j<=20;j++)for(int i=1;i+(1<<(j-1))<=n;i++)
        ma[i][j]=Ma(ma[i][j-1],ma[i+(1<<(j-1))][j-1]),
        mb[i][j]=Mb(mb[i][j-1],mb[i+(1<<(j-1))][j-1]);
}
ll Ga(ll l,ll r)
{
    ll k=log2(r-l+1);
    return Ma(ma[l][k],ma[r-(1<<k)+1][k]);
}
ll Gb(ll l,ll r)
{
    ll k=log2(r-l+1);
    return Mb(mb[l][k],mb[r-(1<<k)+1][k]);
}
ll Ans(ll l,ll r)
{
    if(l==r)return 0;
    ll pl=Ga(l,r),pr=Gb(l,r);
    if(pl>pr)swap(pl,pr);
    return Ans(l,pl)+1+Ans(pr,r); 
}
void Solve()
{
    cin>>n;
    for(int i=1;i<=n;i++)cin>>a[i];
    Pre();cout<<Ans(1,n)<<endl;
}
int main()
{
    int T;cin>>T;
    while(T--)Solve();
    return 0; 
}

E

 

 题解：推柿子题。

手玩数据发现每行的答案都是组合数。

具体的，对于第 $i$ 行第 $j$ 个，答案是 $C(i+j-2,i-1)$ ，对于每一行求和。

运用上指标求和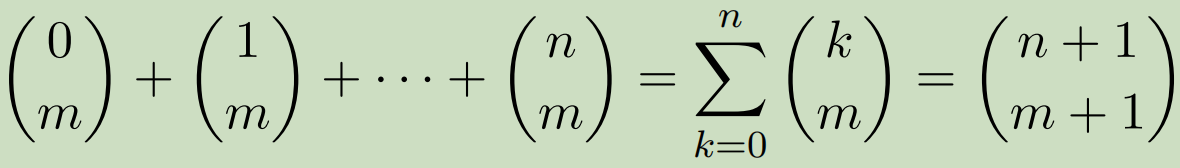

 

 

也就是 $C(i+ai-1,i)$。

#include<bits/stdc++.h>
using namespace std;
 
typedef long long ll;
const ll N=1e6+3,H=1e9+7;
ll n,a[N],jc[N],ij[N],iv[N];
void Pre()
{
    jc[0]=ij[0]=iv[0]=iv[1]=1;
    for(int i=2;i<N;i++)iv[i]=H-(H/i)*iv[H%i]%H;
    for(int i=1;i<N;i++)
        jc[i]=jc[i-1]*i%H,ij[i]=ij[i-1]*iv[i]%H;
}
ll C(ll n,ll m)
{
    if(n<0||m<0||n<m)return 0;
    return jc[n]*ij[m]%H*ij[n-m]%H;
}
void Solve()
{
    cin>>n;ll s=0;Pre();
    for(int i=1;i<=n+1;i++)cin>>a[i];
    for(int i=1;i<=n+1;i++)s=(s+C(i+a[i]-1,i))%H;
    cout<<s<<endl;
}
int main()
{
    int T;T=1;
    while(T--)Solve();
    return 0; 
}

F

 

 不会，咕咕咕

G

 

 不会，咕咕咕

H

 

 不会，咕咕咕