ABC113_D题解

ABC113D题解

题意

给定 \(m\) 条纵向竖线，横向被划分为了 \(n\) 个单位长度，现在从最左上角的点出发，沿着横线向下走，可以在相邻的竖线之间画横线，当遇到横线的时候就会向横线的方向转向。可以任意画线，唯一要求是不能存在两个有公共端点的横线。求最后停在第 \(k\) 条竖线的方案数。

分析

考试的时候一直往计数的方向思考，以为差点就能做出来了，最后快写完了发现有一个小细节处理不了，导致会多算几种情况，于是这个路线就全错了。

非计数即 dp，但是这个题的状态设计对我来说好像有点困难，可以发现不能沿用网格图dp的方式来设计状态，由于本题可以左右下三个方向移动，所以这是一定会引入环的。所以大概只能以 \(n\) 的坐标作为阶段，位于的竖线编号作为状态，那么位于 \((i,j)\) 的时候，有三种转移，也就是 \(i-1\) 行的 \(j-1,j,j+1\) ，其转移情况如下图所示：

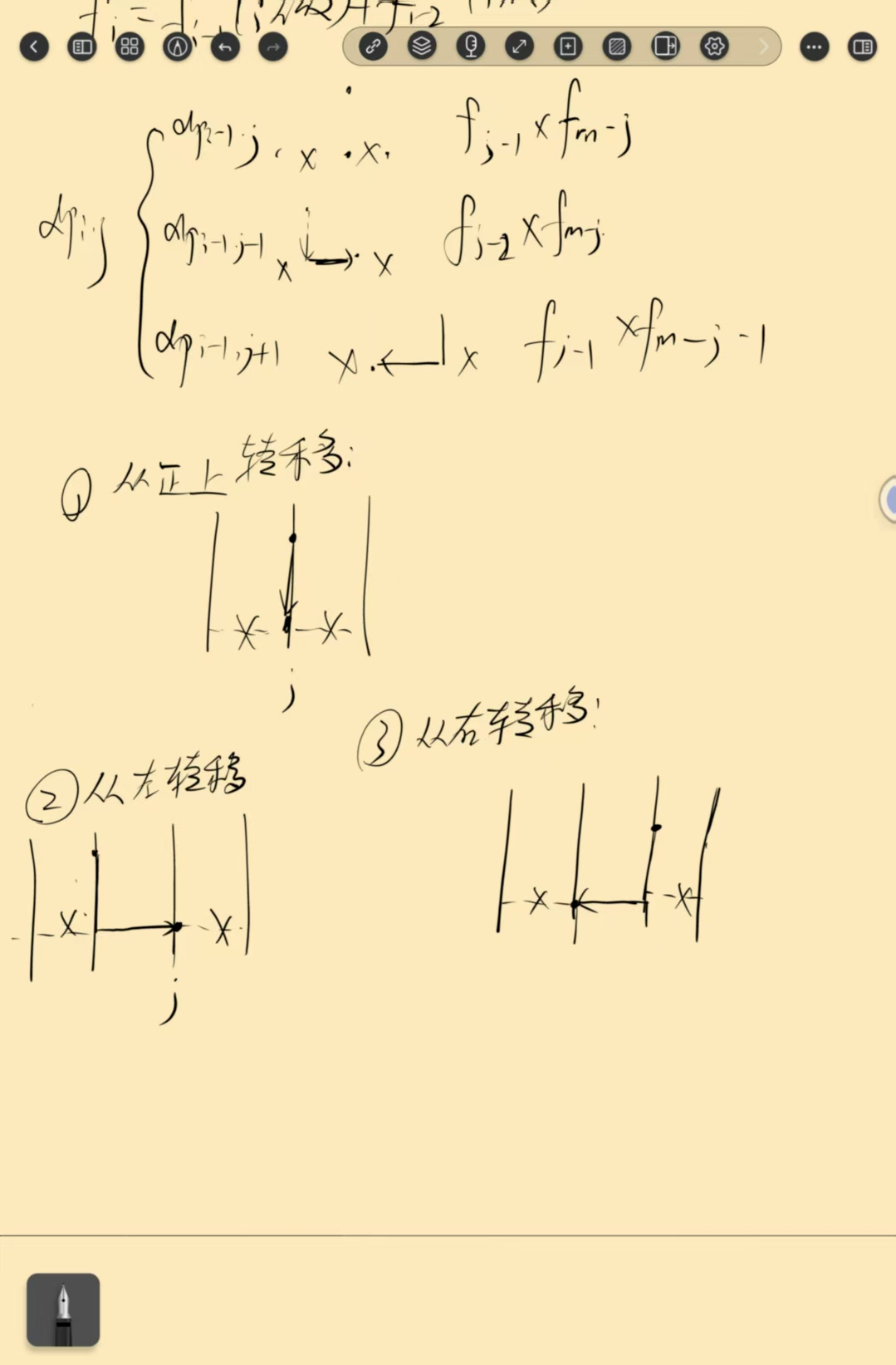
这里我们可以直接状压枚举当前行的画线情况，然后暴力 check 一下是否符合转移条件，不过并不是最优秀的复杂度。

由于这个合法分布情况数实际上对于每一个转移都是相同的，没必要每次都去枚举二进制数。那么还有一种方法就是预先计算出转移系数 \(f\)，我们需要考虑如何递推地求出 “有 \(1\) 行， \(i\) 根竖线时的合法画线数量” 。
如果说第 \(i\) 个位置不划线，那么直接从 \(f_{i-1}\) 转移就行了；
同理，第 \(i\) 个位置划了线，那么就从 \(f_{i-2}\) 转移。
所以递推式为 \(f_i=f_{i-1}+f{i-2}\)，即 \(f_0=1,f_1=1\) 的斐波那契数列。

至此，思路就清晰了。

Code

#include<bits/stdc++.h>
using namespace std;
#define int long long 
const int N=110;
const int MOD=1e9+7;
int f[N];
int dp[N][N];
int n,m,k;
inline void init()
{
    f[0]=f[1]=1;
    for(int i=2;i<=50;++i)
        f[i]=f[i-1]+f[i-2],f[i]%=MOD;
    
}
inline void solve()
{
    cin>>n>>m>>k;
    init();
    dp[0][1]=1;
    for(int i=1;i<=n;++i)
    {
        for(int j=1;j<=m;++j)
        {
            dp[i][j]=dp[i-1][j]*f[j-1]%MOD*f[m-j]%MOD;
            dp[i][j]+=dp[i-1][j-1]*f[j-2]%MOD*f[m-j]%MOD,dp[i][j]%=MOD;
            dp[i][j]+=dp[i-1][j+1]*f[j-1]%MOD*f[m-j-1]%MOD,dp[i][j]%=MOD;
        }
    }
    cout<<dp[n][k];
}
signed main()
{
    ios::sync_with_stdio(0);
    cin.tie(0);
    return solve(),0;    
}