比赛链接:
https://codeforces.com/contest/1644
C. Increase Subarray Sums
题目大意:
给定一个长为 \(n\) 的序列和一个 \(x\),你可以选择序列中的 \(k\) 个元素,让它们都加上 \(x\),然后求最大连续子序列和。输出 \(k\) 从 0 到 \(n\) 的所有的所有答案。
思路:
求最大连续子序列和,可以想到 \(dp\),定义 f[i] 为长度为 i 的连续子序列和的最大值,那么我们的最终结果就是在这个基础上加上 \(k\) 个 \(x\)。
先预处理一下前缀和。接着以 i 为起点,j 为终点,计算出长度从 1 到 n 的连续子序列的最大值。完成第一步。
然后我们加入 \(x\),数量从 0 到 \(n\),计算出最大值。
代码:
#include <bits/stdc++.h>
using namespace std;
#define IOS() ios_base::sync_with_stdio(false);cin.tie(0);cout.tie(0);
const int N = 5e3 + 10, INF = -1e9;
int T, n, x, a[N], s[N], f[N];
void solve(){
cin >> n >> x;
for (int i = 1; i <= n; ++ i){
cin >> a[i];
s[i] = s[i - 1] + a[i];
f[i] = INF;
}
for (int i = 1; i <= n; ++ i)
for (int j = i; j <= n; ++ j)
f[j - i + 1] = max(f[j - i + 1], s[j] - s[i - 1]);
for (int k = 0; k <= n; ++ k){
int ans = 0;
for (int j = 1; j <= n; ++ j)
ans = max(ans, f[j] + min(k, j) * x);
cout << ans << " \n"[k == n];
}
}
int main(){
IOS();
cin >> T;
while (T--)
solve();
return 0;
}
D. Cross Coloring
题目大意:
\(n * m\) 的网格,刚开始涂满白色,现在有 \(k\) 个颜色,\(q\) 次操作,第 \(i\) 次操作选择其中一个颜色对 \(x_i\) 行和 \(y_i\) 列进行涂色,问最后会出现多少个不同的网格,答案对 998244353 取模。只要两个网格中有一个格子的颜色不同,那么这两个网格就是不同的。
思路:
因为前一个操作有可能会被后一个操作覆盖,即某些格子不论之前涂了什么颜色,都对最后的结果没有影响,所以我们反过来考虑。这样子覆盖的情况就不会出现了。
当有新行或者新列出现的时候,说明这个行或者列的格子的颜色就是网格最后的颜色,我们计算进答案,否则不计算。
要考虑一个情况,当所有行或者所有列都涂上颜色的时候,当前答案就已经是最后的结果了。
代码:
#include <bits/stdc++.h>
using namespace std;
#define IOS() ios_base::sync_with_stdio(false);cin.tie(0);cout.tie(0);
#define LL long long
const int mod = 998244353;
LL T, n, m, k, q;
void solve(){
cin >> n >> m >> k >> q;
vector <LL> x(q), y(q);
for (int i = 0; i < q; ++ i)
cin >> x[i] >> y[i];
set <LL> a, b;
LL ans = 1;
for (int i = q - 1; i >= 0; -- i){
if (!a.count(x[i]) || !b.count(y[i])) ans = (ans * k) % mod;
a.insert(x[i]);
b.insert(y[i]);
if (a.size() == n || b.size() == m) break;
}
cout << ans << "\n";
}
int main(){
IOS();
cin >> T;
while(T--)
solve();
return 0;
}
E. Expand the Path
题目大意:
\(n * n\) 的网格,左上角坐标为(1,1),右下角坐标为(n,n),机器人从左上角出发,给一个只包含 'D' 和 'R' 的字符串,'D' 表示向下移动,'R' 表示向右移动,你可以进行任意次修改,每次修改可以选择一个 'R' 或者 'D',使其变成两个字符,即让 'R' 变成 'RR' 或者让 'D' 变成 'DD'。不同的修改法可以让机器人经过不同的格子,求机器人最后能经过几个格子。
思路:
当字符串中只有一种字符时,不论怎么修改,机器人也只能经过 \(n\) 个格子。
当 'R' 和 'D' 都有时,看一个图(嫖题解的)。
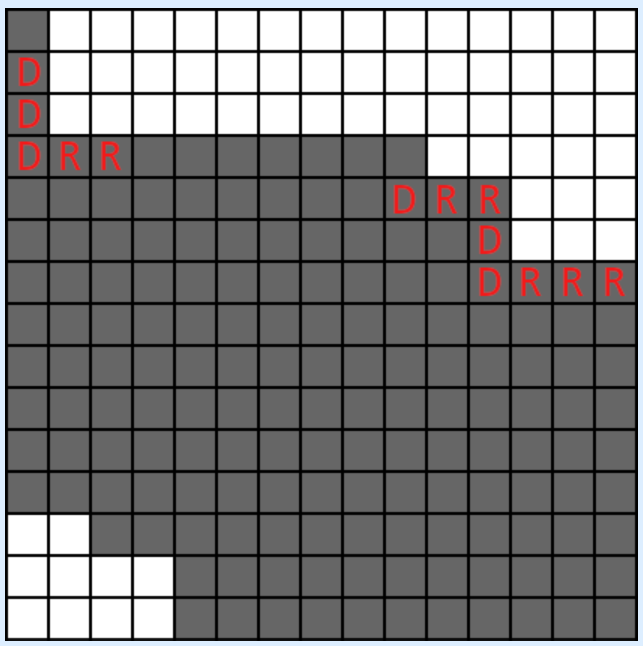
最后的答案就是黑色的格子,黑色的格子不太好计算,所以考虑总格子数减去白色的格子数。从图中可以知道,白色格子分两块,左下角和右上角。
考虑左下角的白格子,记当前为第 \(i\) 个字符,在这之前有 \(r\) 个 'R' 字符。当当前字符是 'R' 的时候,格子被黑色覆盖,当字符是 'D' 的时候,就会有 \(r\) 个白色格子出现。左上角的计算也一样。
但是这样子的计算会有遗漏,它只计算了字符串大小内的白色格子,而外面的格子没有计算。例如字符串长度为 \(s\),那么这只计算了 \(s * s\) 大小的网格中的白色格子。
记字符串刚开始的字符是 \(a_1\),后面变成了 \(a_2\),每次改变下标就 + 1,那外面的格子是由于 \(a_2\) 无限修改后空余出来,所以只用计算 \(a_1\) 的数量,就可以求出外面白色格子的数量。
代码:
#include <bits/stdc++.h>
using namespace std;
#define LL long long
LL T, n;
string s;
void solve(){
cin >> n >> s;
LL r = 0, d = 0, res = 0, p = 0, q = 0;
for (int i = 0; i < s.size(); ++ i)
if (s[i] == 'R') r++;
else d++;
if (r == 0 || d == 0){
cout << n << "\n";
return;
}
r = 0, d = 0;
for (int i = 0; i < s.size(); ++ i){
if (s[i] == 'R') r++;
else res += r, d++;
}
for (int i = 0; s[i] == 'R'; ++ i) p++;
if (s[0] != 'D') res += (n - d - 1) * p;
r = 0, d = 0;
for (int i = 0; i < s.size(); ++ i){
if (s[i] == 'D') d++;
else res += d, r++;
}
for (int i = 0; s[i] == 'D'; ++ i) q++;
if (s[0] != 'R') res += (n - r - 1) * q;
cout << n * n - res << "\n";
}
int main(){
cin >> T;
while (T--)
solve();
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号