Codeforces Round 980 (Div. 2)
A. Profitable Interest Rate
题意:
Alice有 \(a\) 元钱。
银行有两种业务:
- 业务A:存钱,但是要求最少要存 \(b\) 元
- 业务B:花费x元,使得业务A中的要求 \(b\) 减少 \(2*x\) 元
求Alice最多可以存多少钱
分析
如果Alice要存钱,要使得\((ans=a-x)\)就要大于业务A的要求
那么当 \(x\) 取得最小值时,\(ans\) 最大,即 \(ans= max(a - max(b - a, 0),0)\);
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
void solve()
{
ll a, b;
cin >> a >> b;
cout << max(0ll,a - max(0ll, b - a)) << endl;
}
signed main()
{
ios::sync_with_stdio(false);
cin.tie(0),cout.tie(0);
cout << setprecision(11) << fixed;
int t;t=1;
cin>>t;
for(int i=1;i<=t;i++){
//printf("Case %d: ",i);
solve();
}
}
B. Buying Lemonade
题目
有一台柠檬水自动售货机。机器上有 \(n\) 个槽位和 \(n\) 个按钮,每个槽位对应一个按钮,但你并不知道每个按钮对应的是哪个槽位。
当您按下第 \(i\) 个按钮时,有两种可能的事件:
- 若 \(i\) 号槽位有至少一瓶柠檬水,则其中一瓶柠檬水会从这个槽位里掉下来,然后你会把它取走。
- 若 \(i\) 号槽位没有柠檬水,则什么都不会发生。
柠檬水下落速度很快,因此您看不清它从哪个槽位掉出。您只知道每个槽位中瓶装柠檬水的数量 \(a_i (1 \le i \le n)\)。
您需要求出至少收到 \(k\) 瓶柠檬水的最小按按钮次数。
数据保证机器中至少存在 \(k\) 瓶柠檬水。
分析
很简单的一个策略,第一轮按下所有的按钮, 之后每一轮的只按上一轮中,有罐头落下的按钮。这样可以保证在最坏情况下按按钮次数最少。
在这种操作方式下,我们在第 \(i\) 轮会获得饮料的数量\(x\) 即\(a数组中大于等于i的元素个数\),按按钮的次数会在\(x\)的基础上多出\(y\) ,即\(a数组中等于i-1元素的个数\),
但是我们并不能一轮一轮模拟,所以我们将\(a\)数组递增排序,相当于是按照按钮被使用完的顺序先后遍历。
统计一下在使用完了第 \(i\) 个按钮后,还需要多少罐头 \(k\),以及现在按了多少次按钮 \(ans\),
每次计算在 \(i-1\) 按钮使用时,到 \(i\) 个按钮使用完时,可以获得的罐头数量 \(w\) ,即 \((a[i] - a[i - 1])*(n - i + 1)\),
那么本次操作次数就是在这次获得的罐头数加上前一个按钮被确定用完的那一下,当然 \(i=1\) 时没有上一个按钮。
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
#define endl "\n"
void solve()
{
int n, k; cin >> n >> k;
vector<ll> a(n + 1, 0);
for(int i = 1; i <= n; i ++) cin >> a[i];
sort(a.begin() + 1, a.end());
ll ans = 0;
for(int i = 1; i <= n; i ++) {
ll w = 1ll * (a[i] - a[i - 1]) * (n - i + 1);
if(k <= w) {
ans += k + (i != 1);
break;
} else {
ans += w + (i != 1);
k -= w;
}
}
cout << ans << endl;
}
signed main()
{
ios::sync_with_stdio(false);
cin.tie(0),cout.tie(0);
cout << setprecision(11) << fixed;
int t;t=1;
cin>>t;
for(int i=1;i<=t;i++){
//printf("Case %d: ",i);
solve();
}
}
C. Concatenation of Arrays
题目
给定n对数,构造一个排列,使得对应的一个2n序列逆序对的数量最小。
输出这个序列
分析
结论,先按min递增排序,再按max递增排序
我的证明:
每对数内部的逆序对数量不可能被我们改变,所以我们只用考虑不同对之间逆序关系
设2个数对分别是{a,b},{c, d}
因为数对内部关系不用考虑,所以可以认为 a<b, c<d
那么可以产生逆序对的可能只有{a,c},{a,d},{b,c},{b,d};
前2种逆序对在这种排序下不可能产生
然后不会证明了,
这里因为笔者水平有限,只提供一种可能可行的证明方法
假设一个逆序对数目最小的序列是p,在逆序对数量不变的前提下,可以通过交换数对,将数列改成满足我们结论的样子
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<int,int>PII;
const int N=1e6+10;
const int mod=998244353;
const int INF = 0x3f3f3f3f;
const ll INFll = 0x3f3f3f3f3f3f3f3f;
#define endl "\n"
//vector<vector<int>>adj(N);
void solve()
{
vector<PII> v;
int n; cin >> n;
for(int i = 0; i < n; i ++) {
int x, y; cin >> x >> y;
// if(x > y) swap(x,y);
v.push_back({x, y});
}
sort(v.begin(), v.end(),[&](PII a, PII b){
if(min(a.first, a.second) != min(b.first, b.second)) {
return min(a.first, a.second) < min(b.first, b.second);
}
return max(a.first, a.second) < max(b.first, b.second);
});
for(int i = 0; i < n ; i ++) {
cout << v[i].first << " " << v[i].second << " ";
}
cout << endl;
}
signed main()
{
ios::sync_with_stdio(false);
cin.tie(0),cout.tie(0);
cout << setprecision(11) << fixed;
int t;t=1;
cin>>t;
for(int i=1;i<=t;i++){
//printf("Case %d: ",i);
solve();
}
}
D. Skipping
题目
现在已经是 \(3024\) 年,问题的创意早已枯竭,奥林匹克竞赛现在以修改后的个人形式进行。奥林匹克竞赛由 \(n\) 个问题组成,编号从 \(1\) 到 \(n\) 。 \(i\) -th 问题有自己的分数 \(a_i\) 和一定的参数 \(b_i\) ( \(1 \le b_i \le n\) )。
最初,测试系统会给参与者第一个问题。当参与者得到 \(i\) 号问题时,他们有两个选择:
-- 他们可以提交问题并获得 \(a_i\) 分;
- 他们可以跳过问题,在这种情况下,他们将永远无法提交问题。
然后,测试系统会从指数为 \(j\) 的问题中为参与者选择下一个问题,这样,参与者就可以提交下一个问题:
- 如果他提交了 \(i\) -th 问题,系统就会查看索引为 \(j \lt i\) 的问题;
- 如果他跳过了 \(i\) -th问题,则会查看索引为 \(j \leq b_i\) 的问题。
在这些问题中,它会选择一个索引最大的问题,这个索引以前没有给过参与者(他以前既没有提交也没有跳过这个问题)。如果没有这样的问题,那么该参赛者的比赛结束,其成绩等于所有提交问题的分数总和。特别是,如果参赛者提交了第一个问题,那么他们的比赛就结束了。需要注意的是,参赛者最多只能收到每个问题1次。
普罗克霍尔已经为奥林匹克竞赛做了充分准备,现在他可以提交任何问题。请帮助他确定他能获得的最高分数。
分析
假设现在正在回答第 \(i\) 题,每次回答后的下一题就是小于 \(i\) 的最后一题,
那么就意味着我现在只用一直回答,可以拿到所有小于等于 \(i\) 题的所有分数.即某个前缀的分数
同时,当 \(b_i \leq i\)时,必然不可能跳过该题,因为可以只做题,在不丢失分数情况下,使题目来到bi之内最后一个没有遇到的问题,这和之间跳过i题得到的题号是一样的
所以跳题操作只可能发生在 \(i \lt b_i\) 的时候
这里两种做法
- 做法1:dp
dp[i]表示走到 \(i\) 这个点的最小花费,当我们选择不答这个题时,这个题的分数就是花费
如何转移呢?
这里要注意的一点就是,可能存在一种情况,\(i<j<bi<bj\)
我们可以先跳题到\(b_i\),再做题到达\(j\),最后跳到\(b_j\)
所以在 \(i\) 题进行转移时,必须转移到\([i + 1,b_i]\)区间内的所有题目
但是这样光转移的复杂的就是o(n)了,接受不了
换个方向考虑,对应dp[j],我们只需要最小花费的那次转移
假设 dp[j] 由 dp[i] 转移过来:
根据前面的分析和跳题的要求
可以得到
那么我们就可以使用优先队列q来挑选满足条件中,花费最小的转移
条件1是作为可以加入q的最基本的条件。
条件3保证转移一定来自前面的题,所以递增枚举,保证了没有后效性。
剩下的条件2 ,我们只要维护队首元素是否满足条件,当发现队首的 \(bi<j\) 时, 这个转移就再也不可能有用了,因为\(bi<j<j+1\),以后也不可能用上。
最后答案就是所有的位置的前缀和加上这个位置的花费,取一个最大的
- 做法2:最短路
这种思路是差不多的
但是感觉不那么抽象
假设现在正在\(i\)题
- 如果选择回答,那么建一条 \(i \longrightarrow (i-1)\)的边,花费是\(0\)
- 选择跳过,那么就建一条 \(i \longrightarrow bi\) 的边, 花费是\(a_i\);
这样到每个点的最短路dis就是方法一所求的dp
最后统计答案同理
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<ll,int>PII;
const int N=1e6+10;
const int mod=998244353;
const int INF = 0x3f3f3f3f;
const ll INFll = 0x3f3f3f3f3f3f3f3f;
#define endl "\n"
vector<vector<PII>>adj(N);
ll a[N], b[N], s[N];
void solve()
{
int n; cin >> n;
for(int i = 1; i <= n; i ++) cin >> a[i], s[i] = s[i - 1] + a[i];
for(int j = 1; j <= n; j ++) cin >> b[j];
vector<ll> dp(n + 1, INFll);
dp[1] = 0;
priority_queue<PII,vector<PII>,greater<PII> > q;
q.push({a[1], b[1]});
for(int j = 2; j <= n; j ++) {
while(q.size() && q.top().second < j) q.pop();
if(!q.size()) break;
dp[j] = q.top().first;
if(b[j] > j) q.push({dp[j] + a[j], b[j]});
}
ll ans = 0;
for(int i = 1; i <= n; i ++) ans = max(ans, s[i] - dp[i]);
cout << ans << endl;
}
void solve2()
{
int n; cin >> n;
for(int i = 1; i <= n; i ++) adj[i].clear();
for(int i = 1; i <= n; i ++) cin >> a[i], s[i] = s[i - 1] + a[i];
for(int j = 1; j <= n; j ++) cin >> b[j];
vector<ll> dis(n + 1, INFll);
dis[1] = 0;
priority_queue<PII,vector<PII>,greater<PII> > q;
q.push({0, 1});
for(int i = 1; i <= n; i ++) {
if(b[i] > i) adj[i].push_back({b[i], a[i]});
if(i != 1) adj[i].push_back({i - 1, 0});
}
while(q.size()) {
auto [W , u] = q.top(); q.pop();
if(W > dis[u]) continue;
for(auto [v, w] : adj[u]) {
if(W + w < dis[v]) {
dis[v] = W + w;
q.push({dis[v], v});
}
}
}
ll ans = 0;
for(int i = 1; i <= n; i ++) ans = max(ans, s[i] - dis[i]);
cout << ans << endl;
}
signed main()
{
ios::sync_with_stdio(false);
cin.tie(0),cout.tie(0);
cout << setprecision(11) << fixed;
int t;t=1;
cin>>t;
for(int i=1;i<=t;i++){
//printf("Case %d: ",i);
solve();
}
}
E. C+K+S
感觉这个题非常需要思维,笔者一开始拿着题猛猛地猜了几个结论,并且证明了大部分,然后发现最关键的东西没证明出来
题目
给定2个强连通有向图,每个图 \(n\) 个点,但可能有不同数量的边,保证图中每个环的长度都是 \(k\) 的倍数
将 \(2n\) 个点划分成两类
每个顶点都属于两种类型中的一种:传入或传出。对于每个顶点,它的类型都是已知的。
您需要确定是否有可能在源图之间绘制恰好 \(n\) 条有向边,从而满足以下四个条件:
- 任何添加的边的两端都位于不同的图中。
- 从每个传出顶点,正好有一条新增边产生。
- 在每个进入的顶点中,正好有一条添加边进入。
- 在生成的图中,任何循环的长度都能被 \(k\) 整除。
问是否可能可以构造
分析
题目的结论
对于一个强连通有向图,其中所有循环的长度都是 \(k\) 的倍数, 一定可以用 \(k\) 种颜色来将所有点染色,使得每条边都是 \(color_i -> color_{(i+1)\%k}\)
笔者的理解的是:对于图上任意一条简单路径,都可以直接按照顺序循环染色,而所有的简单回路的长度都是 \(k\) 的倍数,也是可以完成的,而强连通这个条件在这里好像没有用
现在对题目给定的两个图,分别取名为图 A,图B
我们先将图A,图B,分别染好颜色,并且都使用的是\([0,k)\)这个区间的颜色编号
对于A中的出点,假设它颜色是i,那么它就要连向B中一个颜色为\((i+1)\%k\)的入点,
对于A中的入点,假设它颜色是i,那么它就要来自B中一个颜色为\((i-1+k)\%k\)的出点,
我们可以直接固定好A的颜色,判断B是否有对于的颜色选择使得所有边全部满足
假设存在一种对应方案
现在我们来证明,为什么这样连边可以使得所有环都是k的倍数
将我们建的边命名为新边,由图A->图B的边是A类边,反之叫做B类边
任意一个A类边和一个B类边称为做一对新边
如果一个环经过了A类边,那么必然要再经过B类边回来,不然不可能形成回路
充分性
我们将所有简单环分为3类:
- 0类环:经过0对新边
- 1类环:经过1对新边
- 2类环:经过2对及以上的新边
对于0类环,他们就是2个图内部就有的环,题目保证他们合法
对于1类环,码字太麻烦了,直接看笔者的手书
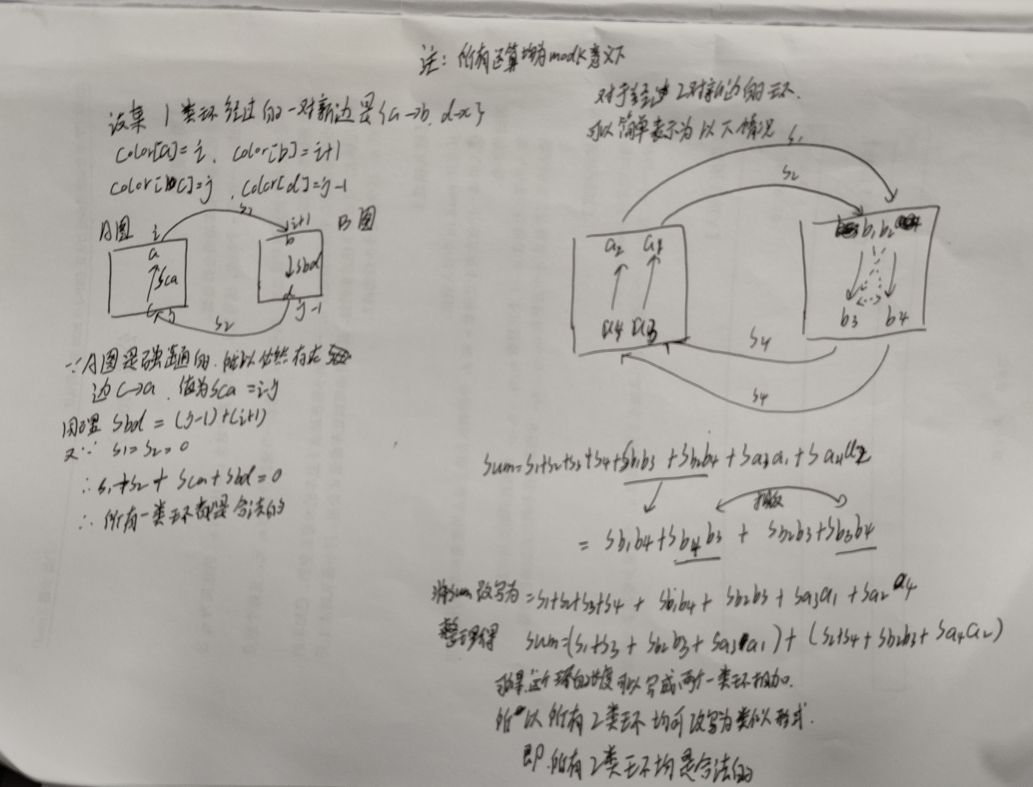
必要性
对于我们使用新边连接的A和B的结合体,我们称为图C,
如果说图中只有A类边或者B类边,那么就不可能有1类环和2类环,那么这个图肯定是合法的
否则,因为A和B都强连通,所有C也必然会强连通,同时,所有环都是k的倍数,根据一开始的结论,必然可以使用k种颜色进行染色
最后就是关键部分了,怎么判断存在对应方案
首先记录A图中[0,k-1]每种颜色的出点和入点数量
然后计算B图中每种颜色i的点需要连接了多少颜色为\((i-1+k)\%k\)的出点, 以及多少颜色为\((i+1)\%k\)的入点,
判断是否存在一个对于B颜色的循环左移,和可以对应上A的要求
具体实现可以将出点入点的数量要求哈希成一个要求,然后将B的结果扩展2倍,变成一个简单的字符串判断问题。
笔者使用了哈希加二分判断判断B每个位置与A对应最长的公共前缀,判断这个长度是否可以达到 \(k\)
当然也可以直接使用扩展\(kmp\)
证明可能有点问题,欢迎指正
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<int,int>PII;
const int N=1e6+10;
const int mod=998244353;
const int INF = 0x3f3f3f3f;
const ll INFll = 0x3f3f3f3f3f3f3f3f;
#define endl "\n"
#define x first
#define y second
int n, k;
int num[3][2];
vector<ll> gets(int flag) {
vector<int> a(n + 1, 0);
vector<vector<int>>adj(n + 1);
for(int i = 1; i <= n; i ++) cin >> a[i],num[flag + 1][a[i]]++;
int m; cin >> m;
for(int i = 1; i <= m; i ++) {
int u, v;
cin >> u >> v;
adj[u].push_back(v);
}
vector<bool> vis(n + 1, false);
vector<int> color(n + 1, 0);
auto dfs = [&] (auto self, int u) -> void {
if (vis[u]) return;
vis[u] = true;
for (int v : adj[u]) {
color[v] = (color[u] + 1) % k;
self(self, v);
}
return;
};
dfs(dfs, 1);
vector<int> in(k, 0), out(k, 0);
for(int i = 1; i <= n; i ++) {
if(a[i]) out[color[i]] ++;
else in[color[i]]++;
}
vector<ll> res;
for(int i = 0; i < k; i ++) {
ll u = in[i] * 100010ll + out[i];
if(flag) {
u = out[(i - 1 + k)%k] * 100010ll + in[(i + 1) % k];
}
res.push_back(u);
}
return res;
}
typedef unsigned long long ull;
ull h1[N],h2[N],p[N];
const ull P = 1000000000000711;
ull get1(int l, int r) {
return h1[r] - h1[l - 1] * p[r - l + 1];
}
ull get2(int l, int r) {
return h2[r] - h2[l - 1] * p[r - l + 1];
}
vector<ll> z_function (const vector<ll>& s) {
ll n = (ll) s.size();
vector<ll> z (n);
for (int i=1, l=0, r=0; i<n; ++i) {
if (i <= r)
z[i] = min (r-i+1ll, z[i-l]);
while (i+z[i] < n && s[z[i]] == s[i+z[i]])
++z[i];
if (i+z[i]-1 > r)
l = i, r = i+z[i]-1;
}
return z;
}
void solve()
{
memset(num, 0, sizeof num);
cin >> n >> k;
auto s1 = gets(0);
auto s2 = gets(1);
if((num[1][1] == n && num[2][0] == n) || (num[1][0] == n && num[2][1] == n)) {
cout << "YES\n";
return;
}
p[0] = 1;
for(int i = 0; i < k; i ++) {
h1[i + 1] = h1[i] * P + s1[i];
h2[i + 1] = h2[i] * P + s2[i];
p[i + 1] = p[i] * P;
}
for(int i = k; i < 2 * k; i ++) {
h2[i + 1] = h2[i] * P + s2[i - k];
p[i + 1] = p[i] * P;
}
for(int i = 1; i <= k; i ++) {
int l = 0, r = k;
while(l < r) {
int mid = (l + r + 1) >> 1;
if(get1(1, mid) == get2(i, i + mid - 1))l = mid;
else r = mid - 1;
}
// cout << l << endl;
if(l >= k) {
cout << "YES\n";
return;
}
}
cout << "NO\n";
}
signed main()
{
ios::sync_with_stdio(false);
cin.tie(0),cout.tie(0);
cout << setprecision(11) << fixed;
int t;t=1;
cin>>t;
for(int i=1;i<=t;i++){
//printf("Case %d: ",i);
solve();
}
}




 浙公网安备 33010602011771号
浙公网安备 33010602011771号