Manacher 学习笔记

简介

Manacher 算法可以在 \(\mathcal{O}(n)\) 的时间内，求出一个长度为 \(n\) 的字符串的最长回文子串。

一些操作与定义

预操作

在开始之前，我们先对这个字符串进行一些处理.

假设我们有字符串 \(s=\text{abbacd}\)。我们把它每一位中间加一个“奇怪的字符”。这个奇怪的字符在原字符串中不能存在，常用的就是 \(\text{#}\) 或 \(\text{\$}\)。这里我使用 \(\text{#}\)，字符串就变成了 \(s=\text{#a#b#b#a#c#d#}\)。

我们为什么要这么做？如果不这么做，如果回文串长度为偶数，那么我们找不到一个回文“中心”（如 \(\text{abba}\)）。但插入后，我们就可以像长度为奇数的回文串一样，找到一个回文“中心”，以免分类讨论。

显然这样操作过后，最后答案要除以二下取整。

定义

1. 回文串：正着读和反着读都一样的串。
2. 回文子串：正着读和反着读都一样的子串。
3. 回文中心：一个回文串正中位置。
4. 回文直径：回文串长度。
5. 回文半径：\(\left\lceil\dfrac{回文直径}{2}\right\rceil\)，如回文串 \(\text{ccfcc}\) 的回文半径是 \(3\)。

过程

我们不难想出一种 \(\mathcal{O}(n^2)\) 的中心扩展法。

枚举每个回文中心位置 \(i\)，看最多能向两边扩展多少。比如 \(\text{abababb}\)，我们枚举到第 \(4\) 个位置为中心，发现可以扩展到 \(\text{babab}\) 然后就把答案更新。

但是这样我们会进行很多次重复的扩展。怎么减少？

Manacher 需要以每个位置为回文中心的最大回文半径，我们记为 \(p_i\)。假设当前我们正在计算 \(p_i\)，那么我们一定已经把 \(p_1\sim p_{i-1}\) 的答案算完了。我们还需记录一个特殊的位置 \(x\)，以这个位置扩展出去的回文串 \([x-p_x+1,x+p_x-1]\) 的右端点最大。我们记这个最右的右端点为 \(R\)，其对应回文左端点记为 \(L\)。

那么现在算 \(p_i\) 有两种情况：

1. \(i>R\)。
   这时暴力向两侧扩展就行了。
2. \(i\le R\)
   这时可以进行优化。

因为 \(i\) 在回文串 \([L,R]\) 内，所以必有一个和它相同的位置 \(j=2x-i\)，它们关于 \(x\) 对称。

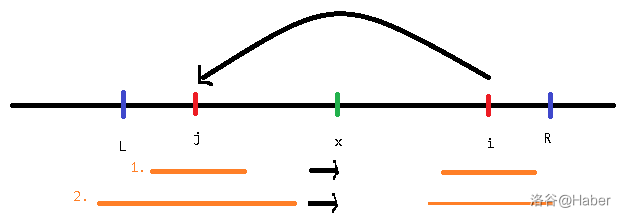
由于 \(j<i\)，那么它的 \(p_j\) 已经计算了。

如果以 \(j\) 为回文中心的回文串不包含 \(L\)（如图中橙 \(1\)），那么 \(i\) 肯定也扩展不了了。那么令 \(p_i\gets p_j\)

如果以 \(j\) 为回文中心的回文串包含 \(L\)（如图中橙 \(2\)），那么从 \(L\) 再向外的那一节 \(i\) 就不能适用了。令 \(p_i\gets R-i+1\) 后，从 \(R\) 开始进行暴力扩展。

复杂度分析

在 Manacher 中，每次暴力扩展都是有意义的（可以把 \(R\) 推进）。一共只会扩展 \(n\) 次，所以是 \(\mathcal{O}(n)\) 的。

题目

Manacher 模板

点击查看代码

#include<bits/stdc++.h>
using namespace std;
const int N=2e7+7;
char s[N],str[N<<1];
int n,len,R,x;
int ans;
int p[N];
int main(){
	scanf("%s",s+1);
	len=strlen(s+1);
	str[++n]='#';
	for(int i=1;i<=len;i++) str[++n]=s[i],str[++n]='#';
	for(int i=1;i<=n;i++){
		p[i]=i>R?1:min(R-i+1,p[2*x-i]);
		while(i-p[i]>=1&&i+p[i]<=n&&str[i-p[i]]==str[i+p[i]]) p[i]++;
		if(i+p[i]-1>R) R=i+p[i]-1,x=i;
		ans=max(ans,p[i]);
	}
	printf("%d\n",(ans*2-1)/2);	//单向为 ans，中心重复算了要 -1
	return 0;
}