DP 学习笔记

Œ# 前言
这个博客极其有可能烂尾，原因这不是一次性写完的。它在持续更新。

DP 是什么

动态规划 (Dynamic Programming)，一般用于解决最优化或计数问题。其主要思想就是将问题分解为若干个子问题，再分解子问题，直到递归到初始问题，最后再通过子问题的解得到原问题的解。

一个问题可以使用 DP 来求解，需要满足两个性质：

最优子结构：每一个问题的答案可以通过其子问题的答案直接得出。
无后效性：可以将所有需要求解的子问题按某种顺序依次求解，某个子问题的决策不会影响他之前的子问题的答案。

DP 的各个种类

1. 线性 DP

顾名思义，这是状态之间是线性关系。也是最“质朴”的一类 DP。

1.1 最长上升子序列 LIS

我们设 $f_i$ 表示到 $i$ 这个位置（强制选 $i$）的最长上升子序列长度。为什么强制选 $i$？后面会讲到。

考虑 $i$ 这个位置从什么位置来，所有的 $a_j<a_i(j<i)$ 过来。那么 $f_i={\max{f_j}}+1$。

直接这么转移是 $\mathcal{O}(n^2)$ 的，考虑优化。我们把 $f$ 插进一个树状数组里，维护 $\max$，插入的位置就是 $a_i$ 的值。每次转移就查询小于 $a_i$ 的最大值就行了。这样就变成了 $\mathcal{O}(n\log n)$。

1.2 最长公共子序列 LCS

设 $f_{i,j}$ 表示 $A$ 序列的前 $i$ 个数，$B$ 序列的前 $j$ 个数的最长公共子序列。

那么转移？

当 $A_{i}=B_{j}$ 时，$f_{i,j}=f_{i-1,j-1}+1$。
当 $A_i\neq B_j$ 时，就只能继承了，$f_{i,j}=\max(f_{i,j-1},f_{i-1,j})$。

这个复杂度是 $\mathcal{O}(|A||B|)$。如果 $A,B$ 是排列的时候，则以做到 $\log$。可以见洛谷的题解。

1.3 数字三角形

典题。设 $f_{i,j}$ 为走到 $(i,j)$ 这个位置的最大权值和。

那么 $f_{i,j}$ 可以从它上面的 $f_{i-1,j}$，和左上方的 $f_{i-1,j-1}$ 转移过来，最后要加上权值。

\[f_{i,j}=\max(f_{i-1,j-1},f_{i-1,j})+a_{i,j} \]

1.4 过河卒

这是一个方案计数类的经典题目。

首先我们看状态的定义 $f_{i,j}$ 表示从 $(1,1)$ 走到 $(i,j)$ 的方案数。显然有边界：$i=1$ 或 $j=1$ 时，都只有一种方案。（前提是路径上马跳不到，如果跳得到的话，后面的都是走不到的，方案为 $0$）。

那么我们如何转移？显然走到一个点可以从它上面和左边走来，所以 $f_{i,j}=f_{i-1,j}+f_{i,j-1}$。

注意，如果马能跳到的话，那么 $f_{i,j}$ 应为 $0$。

2. 背包

背包问题是指给定 $n$ 个物品的价值 $v[i]$、体积 $w[i]$，以及一个背包容量 $m$，让你在物品的体积不超过背包容量的情况下，让背包内物品价值最大化。

形式化题意： 给定 $n$ 个 $v[i],w[i]$，以及 $m$。选若干个 $i$ 其中 $\forall i\in[1,n]$，使得 $\sum w[i]\le m$ 并且最大化 $\sum v[i]$。

2.1 01 背包问题

最基础的一类问题。
顾名思义，01背包就是表示每个物品的状态只有选和不选两种（即每个物品只有 $1$ 个），$1$ 即选，$0$ 即不选。那么我们就可以开始设置状态了。
设 $f[i][j]$ 表示我们当前已经选到第 $i$ 个物品了，而我们现在已经用了 $j$ 这么多的背包容量，所获得的价值最大是 $f[i][j]$。

那么我们考虑如何转移。显然第 $i$ 个物品可以选或者不选。
老师我知道！$f[i][j]=\max (不选,选)$ ！
啊对，思路没问题。考虑形式化？
老师我知道！不选就是 $f[i-1][j]$，选就是 $\dots$
啊，好，我们换一位同学。
老师老师我来！选之前的背包容量就是 $j-w[i]$，又因为我们要选它，所以要在后面加上一个价值 $v[i]$，所以这时候柿子就是 $f[i-1][j-w[i]]+v[i]$！
回答的非常好，那我们整合一下就是:

\[f[i][j]=\max (f[i-1][j],f[i-1][j-w[i]]+v[i]) \]

这就是转移式了。
经过几分钟劈里啪啦，代码就大功告成了：

点击查看代码

#include<bits/stdc++.h>
using namespace std;
int n,m;
const int N=2e5+5;
int v[N],w[N];
int f[N][N];
int main(){
	cin>>n>>m;
	for(int i=1;i<=n;i++) cin>>v[i]>>w[i];
	for(int i=1;i<=n;i++)
		for(int j=1;j<=m;j++)
			if(j>w[i])
				f[i][j]=max(f[i-1][j],f[i-1][j-w[i]]+v[i]);
			else
				f[i][j]=f[i-1][j];
	cout<<f[n][m]<<endl;
	return 0;
}

然后就有的同学直接就改了个范围就交上去了，结果你猜怎么着，MLE 了。
怎么改才能 AC 呢？
老师，我发现 $f[i][j]$ 的转移只和 $i-1$ 这一行的值有关，也就是我们只需要存 $2$ 行的值！
嗯，这位同学说的有道理。同学们，其实我们连两行的值都不用存。
你可以发现转移的时候大盖是经过了这个过程：

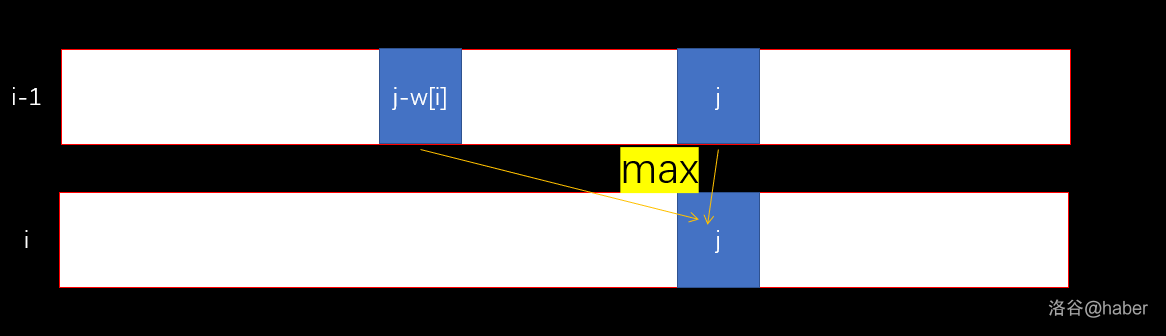
01背包转移示意图

有眼睛的人都会发现，转移只会和上一行 $j$ 之前的值有关，和后面的没半毛钱关系，可以直接覆盖掉。
老师老师，我们可以倒着更新！这样就可以保留前面的值了！
这就是我们想要的一维空间了。

点击查看代码

#include<bits/stdc++.h>
using namespace std;
int n,m;
const int N=2e5+5;
int v[N],w[N];
int f[N];
int main(){
	cin>>n>>m;
	for(int i=1;i<=n;i++) cin>>v[i]>>w[i];
	for(int i=1;i<=n;i++)
		for(int j=m;j>=w[i];j--)
			f[j]=max(f[j],f[j-w[i]]+v[i]);
	cout<<f[m]<<endl;
	return 0;
}

注意更新到 $w[i]$ 就可以停止了，因为 $w[i]$ 之前的值都不会变。

不要质疑你自己，01 背包你就会了。

2.2 完全背包问题

不同于 01 背包的是，完全背包的每一件物品都有无限个。
老师！我可以枚举选取个数！暴力出奇迹！
出是肯定能出，但是能出几个测试点就不知道了。

点击查看代码

#include<bits/stdc++.h>
using namespace std;
int n,m;
const int N=2e5+5;
int v[N],w[N];
int f[N][N];
int main(){
	cin>>n>>m;
	for(int i=1;i<=n;i++) cin>>v[i]>>w[i];
	for(int i=1;i<=n;i++)
		for(int j=0;j<=m;j++)
			for(int k=0;k*w[i]<=j;k++)
				f[i][j]=max(f[i-1][j],f[i-1][j-k*w[i]]+k*v[i]);
	cout<<f[n][m]<<endl;
	return 0;
}

这连 AC 的样子都没装像。
我们具体的来看一下朴素转移逝：

\[f[i][j]=\max (f[i-1][j],f[i][j-w[i]]+v[i],f[i][j-w[i]\times 2]+v[i]\times 2,f[i][j-w[i]\times 3]+v[i]\times 3,\dots) \]

我们把第 $1,2$ 项拿出来看一下，$\max(f[i-1][j],f[i][j-w[i]]+v[i])$。好像啥都干不了。
我们再把 $2,3$ 项拿出来看一下，$\max(f[i][j-w[i]]+v[i],f[i][j-w[i]\times 2]+v[i]\times 2)$ ，咦？不就是在 $f[i-1][j-w[i]]$ 的基础上再选了 $i$ 这件物品吗？
再看 $3,4$ 项，不就是在 $2$ 件物品的时候再选了同 $1$ 个物品吗？Wow!

那么我们就可以总结了，其实无论你选多少件，你其实都是从上一件那里转移过来的，所以你就不必再考虑选多少个的问题。直接来即可。

乱糊的代码：

点击查看代码

#include<bits/stdc++.h>
using namespace std;
int n,m;
const int N=2e5+5;
int v[N],w[N];
int f[N][N];
int main(){
	cin>>n>>m;
	for(int i=1;i<=n;i++) cin>>v[i]>>w[i];
	for(int i=1;i<=n;i++)
		for(int j=w[i];j<=m;j++)
			f[i][j]=max(f[i-1][j],f[i-1][j-w[i]]+v[i]);
	cout<<f[n][m]<<endl;
	return 0;
}

为什么不用和 01 背包一样倒序维护了？~~因为那就和 01 背包一样了。~~

我们此时没有考虑这件物品要取多少件的，我们只知道我们前面的选择时最佳的，此时我们是在加一件上去还是到此止步。我们恰巧需要前面正确的转移，所以必须正序。~~作者尽力了~~

那一维实现就比较简单了：

点击查看代码

#include<bits/stdc++.h>
using namespace std;
int n,m;
const int N=2e5+5;
int v[N],w[N];
int f[N][N];
int main(){
	cin>>n>>m;
	for(int i=1;i<=n;i++) cin>>v[i]>>w[i];
	for(int i=1;i<=n;i++)
		for(int j=w[i];j<=m;j++)
			f[j]=max(f[j],f[j-w[i]]+v[i]);
	cout<<f[m]<<endl;
	return 0;
}

没有难度好吧。

2.3 多重背包问题

这不同于完全背包的是，我们的物品没有无限个了，现在每个物品只有 $c[i]$ 件。那这个问题怎么办呢？

2.3.1 暴力

我会枚举！

点击查看代码

#include<bits/stdc++.h>
using namespace std;
int n,m;
const int N=2e5+5;
int v[N],w[N],num[N];
int f[N];
int main(){
	cin>>n>>m;
	for(int i=1;i<=n;i++) cin>>v[i]>>w[i]>>num[i];
	for(int i=1;i<=n;i++)
		for(int j=m;j>=w[i];j--)
			for(int k=0;k<=num[i]&&k*w[i]<=j;k++)
				f[j]=max(f[j],f[j-w[i]*k]+v[i]*k);
	cout<<f[m]<<endl;
	return 0;
}

非常简单，这里就不在说了。

2.3.2 二进制拆分

你以为这就完了？绝招：二进制拆分

大概是怎么样一个工作原理呢？举个栗子，假设当前这个物品有 $34$ 个，我们可以将这些物品拆成若干个独立的物品。具体拆法：$34=1+2+4+8+16+3$。
为什么要这样拆？大家都知道，一个十进制下的自然数都可以拆成若干个 $2^i$ 之和的形式。以刚才的拆法可以将选 $0,1,2,3,\dots,34$ 个物品的方案都囊括进来。
那么代码实现就比较简单了。

点击查看代码

#include<bits/stdc++.h>
using namespace std;
int n,m,a,b,c,cnt;
const int N=5e5+5;
int v[N],w[N],t[N],f[N];
int main(){
	cin>>n>>m;
	for(int i=1;i<=n;i++){
		int j;
		bool flag=true;
		cin>>a>>b>>c;
		for(j=1;j<=c;j<<=1){
			v[++cnt]=a*j;
			w[cnt]=b*j;
			t[cnt]=j;
			c-=j;
			if(j<<1 != c) flag=true;
			else flag=false;
		}
		if(flag){	//Last part
			v[++cnt]=a*c;
			w[cnt]=b*c;
			t[cnt]=c;
		}
	}
	for(int i=1;i<=cnt;i++)
		for(int j=m;j>=w[i];j--)
			f[j]=max(f[j],f[j-w[i]]+v[i]);
	cout<<f[m]<<endl;
	return 0;
}

2.3.3 单调队列优化

$n,m\le 100$
我会暴力！
$n\le 1000,m\le 2000$
我会二进制优化！
$n\le 1000,m\le 20000$
？？

这时，我们就需要单调队列优化！

容易发现，多重背包就是在完全背包的基础上，给每个物品增加了限制个数 $c_i$。完全背包的转移式是 $f_{i,j}=\max(f_{i-1,j,f_{i-1,j-w_i}+v_i},f_{i-1,j-2w_i}+2v_i,...,f_{i-1,j-sw_i}+sv_i)$。其中 $s=\left\lfloor\dfrac{j}{w_i}\right\rfloor$，即目前在容量为 $j$ 的时候最多能选的个数。

但是，多重背包可能选不了那么多个，上限就是选择 $c_i$ 个。即此时的 $s=\min\left(\left\lfloor\dfrac{j}{w_i}\right\rfloor,c_i\right)$。

发现了吗？每次向后能选的最大长度就是 $c_i$，即滑动窗口的长度就是 $c_i+1$（因为可以不选，选择的区间是 $[0,s]$）。容易发现，这样我们每次更新的 $j$ 是同余于 $w_i$ 的，也就是我们只能先把模 $w_i=0$ 的 $j$ 更新了，再去更新模 $w_i=1$ 的 $j$，一直到模 $w_i=w_i-1$ 的 $j$。

点击查看代码

#include <iostream>
using namespace std;
const int N=1e3+3,M=2e4+4;
int n,m;
int v[N],w[N],c[N];
int f[2][M];
int q[M];
int head,tail;
int main(){
	scanf("%d%d",&n,&m);
	for(int i=1;i<=n;i++) scanf("%d%d%d",w+i,v+i,c+i);
	for(int i=1;i<=n;i++){
		for(int r=0;r<w[i];r++){
			head=0,tail=-1;
			for(int j=r;j<=m;j+=w[i]){
				while(head<=tail&&j-q[head]>c[i]*w[i]) head++;
				while(head<=tail&&f[(i-1)&1][q[tail]]+(j-q[tail])/w[i]*v[i]<=f[(i-1)&1][j]) tail--;
				q[++tail]=j;
				f[i&1][j]=f[(i-1)&1][q[head]]+(j-q[head])/w[i]*v[i];
			}
		}
	}
	printf("%d\n",f[n&1][m]);
	return 0;
}

3. 区间 DP

区间 DP 是定义状态是一个区间的一种 DP。通常定义 $f_{i,j}$ 为完成 $[i,j]$ 这个区间的最大得分/最小花费。

3.1 石子合并

首先断环为链。然后我们以最小得分为例。设 $f_{i,j}$ 为合并 $[i,j]$ 这个区间的最小得分。

考虑转移。通常，我们是枚举一个中间断点 $k$，相当于合并了 $[i,k],[k+1,j]$ 两堆石子，代价为 $sum[i,k]+sum[k+1,j]$。

边界条件为 $f_{i,i}=sum[i,i]$。

点击查看代码

#include<bits/stdc++.h>
using namespace std;
const int N=202;
int sum[N],a[N];
int n;
int f[N][N][2],ans[2];	//f[i][j][0] 为最小值，f[i][j][1] 为最大值
int main(){
	scanf("%d",&n);
	for(int i=1;i<=n;i++) scanf("%d",a+i),a[i+n]=a[i];
	for(int i=1;i<=n*2-1;i++) sum[i]=sum[i-1]+a[i];
	for(int len=2;len<=2*n-1;len++){
		for(int l=1;l+len-1<=2*n-1;l++){
			int r=l+len-1;
			f[l][r][0]=1e9,f[l][r][1]=-1e9;
			for(int k=l;k<r;k++){
				f[l][r][0]=min(f[l][k][0]+f[k+1][r][0],f[l][r][0]);
				f[l][r][1]=max(f[l][k][1]+f[k+1][r][1],f[l][r][1]);
			}
			f[l][r][0]+=sum[r]-sum[l-1],f[l][r][1]+=sum[r]-sum[l-1];
		}
	}
	ans[0]=1e9,ans[1]=-1e9;
	for(int l=1;l<=n;l++){
		int r=l+n-1;
		ans[0]=min(ans[0],f[l][r][0]);
		ans[1]=max(ans[1],f[l][r][1]);
	}
	printf("%d\n%d\n",ans[0],ans[1]);
	return 0;
}

3.2 涂色

老规矩，我们采用 $f_{i,j}$ 表示涂 $[i,j]$ 的总次数。显然 $f_{i,i}=1$。

然后我们发现一个事情，如果 $s_i==s_j$ 那么我们可以用 $f_{i-1,j}$ 或 $f_{i,j-1}$ 向左或者向右多刷 $1$ 个格子得到。

那么如果 $s_i\neq s_j$，那么我们直接枚举断点 $k$，答案取 $\min$。

最后的答案是 $f_{1,n}$。

点击查看代码

#include<bits/stdc++.h>
using namespace std;
string s;
int f[52][52];
int main() {
	int n;
	cin>>s;
    n=s.length();
	memset(f,0x7f,sizeof f); 
	for(int i=1;i<=n;++i) f[i][i]=1;
	for(int l=1;l<n;++l)
		for(int i=1,j=1+l;j<=n;++i,++j) {
			if(s[i-1]==s[j-1]) f[i][j]=min(f[i+1][j],f[i][j-1]);//抹掉 
			else for(int k=i;k<j;++k) f[i][j]=min(f[i][j],f[i][k]+f[k+1][j]);//找断点 
		}
	printf("%d\n",f[1][n]);
	return 0;
}

3.3 关路灯

这题是一个区间 DP 的经典模型。容易发现，关掉的路灯一定在一个区间内。（因为他不可能飞过去关路灯）我们设 $f_{i,j,0/1}$ 表示关完 $[i,j]$ 的灯，并且停留在 $l(0)$ 或者 $r(1)$ 的最小代价。并且这个状态是可以从 $f_{i+1,j,0/1}$ 和 $f_{i,j-1,0/1}$ 转移过来的。那么这个题就很容易做了。最后答案是 $\min(f_{1,n,0},f_{1,n,1})$。

点击查看代码

#include<bits/stdc++.h>
using namespace std;
const int N=55;
int n,c;
int sum[N],d[N],w[N];
int f[N][N][2];
int main(){
	scanf("%d%d",&n,&c);
	for(int i=1;i<=n;i++){
		scanf("%d%d",d+i,w+i);
		sum[i]=sum[i-1]+w[i];
	}
	memset(f,127,sizeof f);
	f[c][c][0]=f[c][c][1]=0;
	for(int i=c;i>=1;i--){
		for(int j=i+1;j<=n;j++){
			f[i][j][0]=min(
			f[i+1][j][1]+(d[j]-d[i])*(sum[n]-sum[j]+sum[i]),
			f[i+1][j][0]+(d[i+1]-d[i])*(sum[n]-sum[j]+sum[i]));
			f[i][j][1]=min(
			f[i][j-1][1]+(d[j]-d[j-1])*(sum[n]-sum[j-1]+sum[i-1]),
			f[i][j-1][0]+(d[j]-d[i])*(sum[n]-sum[j-1]+sum[i-1]));	
		}
	}
	cout<<min(f[1][n][0],f[1][n][1])<<"\n";
	return 0;
}
/*
f[i][j][0](left)
f[i][j][1](right)
*/

3.4 加分二叉树

乍一看是解决树上问题的，咋就是区间 DP？加分二叉树的定义是 $\text{subtree} 的左子树的加分 \times \text{subtree}的右子树的加分 + \text{subtree}的根的分数$。容易发现，因为给出的是中序遍历，所以左子树一定在根的左边，右子树一定在根的右边。我们定义 $f_{i,j}$ 为这个子树的最大加分，那么我们就可以枚举这个子树的根 $k$，其左边 $[i,k-1]$ 就一定是它的左子树，其右边 $[k+1,j]$ 就一定是它的右子树。

那这就很好转移了啊 $f_{i,j}=\max\limits_{i\le k\le j}(f_{i,k-1}\times f_{k+1,j}+score_k)$ ，显然如果 $f_{i,j}$ 的 $i=j$ 时，$f_{i,j}=score_i$，如果 $f_{i,j}$ 中的 $i>j$，则这个子树为空。依照题面，这时分数为 $1$。

答案就是 $f_{1,n}$。至于输出前序遍历，每次转移记录一下当前区间的根节点就行。

点击查看代码

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=33;
int a[N],n;
int rt[N][N];
ll f[N][N];
void print(int l,int r){
	if(l>r) return ;
	printf("%d ",rt[l][r]);
	if(l==r) return ;
	print(l,rt[l][r]-1);
	print(rt[l][r]+1,r);
}
int main(){
	scanf("%d",&n);
	for(int i=1;i<=n;i++) scanf("%d",a+i),f[i][i-1]=f[i+1][i]=1,f[i][i]=a[i],rt[i][i]=i;
	for(int len=2;len<=n;len++)
		for(int l=1;l+len-1<=n;l++){
			int r=l+len-1;
			for(int k=l;k<=r;k++){
				if(f[l][r]<f[l][k-1]*f[k+1][r]+a[k]){
					rt[l][r]=k;
					f[l][r]=f[l][k-1]*f[k+1][r]+a[k];
				}
			}
		}
	printf("%lld\n",f[1][n]);
	print(1,n);
	return 0;
}

4. 树形 DP

顾名思义，就是在树上进行 DP，通常有这样几种定义方式：

$f_{i}$ 树上 $i$ 子树的答案。
$f_{i,0/1}$ 树上 $i$ 子树的答案，其中选了/没选 $i$。
$f_i$ 子树 $i$ 之外的答案。
$f_i$ 表示 $i$ 到根的答案。

4.1 没有上司的舞会

经典题目。树的最大点独立集。设 $f_{i,0/1}$ 表示选了/没选 $i$，子树内的答案。

转移：$$f_{u,0}= \max\limits_{v\in son_u}(f_{v,0},f_{v,1})$$

\[f_{u,1}=score_u+\sum\limits_{v\in son_u}f_{v,0} \]

答案是 $\max(f_{root,0},f_{root,1})$。

点击查看代码

#include<bits/stdc++.h>
using namespace std;
const int N=6e3+3;
int h[N],to[N<<1],ne[N<<1],idx;
int r[N],f[N][2];
int rt,fa[N],n;
void add(int a,int b){
	to[++idx]=b;
	ne[idx]=h[a];
	h[a]=idx;
}
void dfs(int o,int fth){
	f[o][0]=0;
	f[o][1]=r[o];
	for(int i=h[o];i!=-1;i=ne[i]){
		int j=to[i];
		if(j==fth) continue;
		dfs(j,o);
		f[o][0]+=max(f[j][1],f[j][0]);
		f[o][1]+=f[j][0];
	}
}
int main(){
	memset(h,-1,sizeof h);
	scanf("%d",&n);
	for(int i=1;i<=n;i++) scanf("%d",r+i);
	for(int i=1;i<n;i++){
		int x;
		scanf("%d",&x);
		scanf("%d",fa+x);
		add(x,fa[x]),add(fa[x],x);
	}
	for(int i=1;i<=n;i++)
		if(fa[i]==0){
			rt=i;
			break;
		}
	dfs(rt,0);
	printf("%d\n",max(f[rt][0],f[rt][1]));
	return 0;
}

posted @ 2023-10-11 09:00 HaberHanpi 阅读(12) 评论(0) 收藏举报

刷新页面返回顶部

Haber

傻子

DP 学习笔记

DP 是什么

DP 的各个种类

1. 线性 DP

1.1 最长上升子序列 LIS

1.2 最长公共子序列 LCS

1.3 数字三角形

1.4 过河卒

2. 背包

2.1 01 背包问题

2.2 完全背包问题

2.3 多重背包问题

2.3.1 暴力

2.3.2 二进制拆分

2.3.3 单调队列优化

3. 区间 DP

3.1 石子合并

3.2 涂色

3.3 关路灯

3.4 加分二叉树

4. 树形 DP

4.1 没有上司的舞会

公告