ARC188 做题记

A (ABC Symmetry)

题意

对于由 A、B、C 组成的非空字符串 \(T\)，如果可以以任意执行下述操作删空，则称其为 好串。

• 操作 \(1\)：选择 两个相同的字符 并删除。

• 操作 \(2\)：选出 \(A,B,C\) 各一个并删除。

给定一个由 A、B、C、? 组成、长度为 \(N\) 的字符串 \(S\)。

将每个 ? 替换为 A、B 或 C 后，问有多少种字符串，包含 \(\ge K\) 个 好子串，答案对 \(998244353\) 取模。

注意，即使是相同的子串，只要在原字符串中的位置不同，也要分别计数。

\(1\le N\le 50,1\le K\le \dbinom{N}{2}\)

题解

注意到一个子串的好坏之和它 \(A,B,C\) 的个数相关，设为 \(a,b,c\)。

则一个串是好的显然等价于 \(a\equiv b\equiv c\pmod 2\Leftrightarrow 2\mid a+b,2\mid a+c\)。

然后一个串 \(S\) 的好子串个数怎么刻画呢？

相当于把前缀 \((a+b,a+c)\) 二元组 \(\bmod 2\) 写出来，判断有多少对相等。

然后 ddp，记录 \(f_{i,x,y,z,w}\) 表示到 \(i\)，\((0/1,0/1)\) 这四种情况分别有 \(x,y,z,w\) 个的方案数，直接 dp 转移。

做一些剪枝即可，复杂度是小常数 \(\mathcal{O}(n^4)\)，随便过。我偷懒用记忆化搜索实现。

\(\bf{record}\)

B (Symmetric Painting)

题意

\(T\) 组多测，给定 \(N,K\)，解决下述问题：

在圆周上有 \(N\) 个等分的位置，依次标记为 \(0,1,\ldots,N-1\)。

最初，Alice 站在点 \(0\)，Bob 站在点 \(K\)，所有的点都被涂成白色。两人轮流操作，从 Alice 开始，操作规则如下：

• 选择一个当前为白色的点，将其涂成黑色。
  • 但操作后，所有点的颜色关于操作者与圆心连线的对称轴必须保持对称。

如果操作者无法进行满足上述条件的操作，则操作立即终止。

绝顶聪明的两人会协作，请判断在一系列操作全部结束后，是否能将所有点都涂成黑色，输出 \(\text{Yes/No}\) 即可。

\(T\le 10^5,2\le N\leq {\color{red}{10^{18}}},1\le K\lt N\)

题解

你们这帮人抄官方题解都比你们写的东西清楚，真的。

---

现在所有下标 \(\bmod\ N\) 考虑。

Alice 第一步能选择 \(0\) 或当 \(2\mid N\) 时选择 \(\frac{N}{2}\)。

之后 Alice 相当于 \(x\to -x\)，Bob 相当于 \(x\to 2K-x\)。

假设 Alice 从 \(0\) 开始染色，那么染色点的顺序为 \(0, 2K, -2K, 4K, -4K, \ldots\)。

按照这个过程会重复到所有 \(\gcd(N, 2K)\) 倍数的点都被染完。

如果 Alice 可以从点 \(\frac{N}{2}\) 开始染色，那么情况也是类似的。我们把目前的过程称为 一轮。

此时一轮染色了 \(c=\frac{N}{\gcd(N,2K)}\) 个点。

首先 \(\gcd(N,2K)=1\) 则此时染完，先解决掉。

• 如果 \(c\) 是奇数，此时轮到 Bob。

  发现只有当 \(2\mid N\)，并且最后一个点到达 \(K\) 或 \(K+\frac{N}{2}\) 时候才能染对径点开始第二轮。

  否则一定不合法。

  而当 \(2\mid N\) 时，我们最后确实到了 \(-2K\times \dfrac{c-1}{2}=K-\frac{NK}{2\gcd(N/2,K)}\equiv K\pmod {\frac{N}{2}}\)。

  考虑完成第二轮操作后，根据对称性，所有对径点对要么都已染色，要么都未染色。

  此时合法条件是 \(2\mid N,2c=n,c\) 是奇数。即 \(\gcd(N,2K)=2,4\nmid N\)。

• 如果 \(c\) 是偶数，则轮到 Alice。但由于已经染色的点是偶数，Alice 对称轴上的两个点都已经染色好了。因此，操作到此为止，不可能涂完所有点。就坠机了。

综上，合法条件为 \(\gcd(N,2K)=1\) 或 \(\gcd(N,2K=2)\and 4\nmid N\)。

\(\bf{record}\)

C (Honest or Liar or Confused)

题意

给定两个长度为 \(n\) 的 \(01\) 数组 \(a,b\)。

有 \(m\) 个限制 x,y,z：\(a_x\oplus b_x \oplus a_y=z\)，其中 \(\oplus\) 表示异或，\(z\in \{0,1\}\)。

判断是否存在合法的 \(a,b\) 数组，并构造选择 \(a\) 数组的方案。

\(2\le n,m\le 2\times 10^5\)，同一组 \((x,y)\) 不会被限制两次，保证 \(x\neq y\)。

题解

直接令 \(c_x=a_x\oplus b_x\)，然后扩展域并查集表示 \(4n\) 个量 \(W(i,0):c_i=0,W(i,1):c_i=1,W(i,2):b_i=0,W(i,3):b_i=1\)。

然后类似 2-SAT 连边，判断是否 \(W(i,0/1)\) 连通或者 \(W(i,2/3)\) 连通，则不合法。

否则判断 \(W(i,0)\) 与 \(W(i,2/3)\) 的连通性，即可知道 \(a_i=c_i\oplus b_i\)。

注意若 \(W(i,0)\) 与 \(W(i,2/3)\) 均不连通，则钦定 \(a_i=0,b_i=c_i\)，然后重新连边 \(W(i,0)\leftrightarrow W(i,2),W(i,1)\leftrightarrow W(i,3)\)。

\(\bf{record}\)

D (Mirror and Order)

题意

给定 \(N\) 和长度为 \(N\) 的序列 \(A,B\)。

有 \(N\) 个长度为 \(3\) 的数列 \(s_1\sim s_N\)，需要满足这些条件：

• \(\forall k=1,2,3\)，所有数列的第 \(k\) 项中，从 \(1\sim N\) 的整数恰好出现一次。

在这些数列的集合中，我们定义两个数列 \(a=(a_1,a_2,\ldots,a_N)\) 和 \(b=(b_1,b_2,\ldots,b_N)\)，其定义方式如下：

• 设 \(s_i\) reverse 后为 \(t_i\)。当所有的 \(s_i\) 和 \(t_i\) 按字典序排列时，\(s_i\) 排第 \(a_i\)，\(t_i\) 排第 \(b_i\)。

• 如果在这些 \(2N\) 个数列中出现两个或更多完全相同的数列，则 \(a\) 和 \(b\) 无法定义。

因此，当 \(a\) 和 \(b\) 能被定义时，\(a\cup b\) 为 \(1\sim 2N\) 排列。

给定一个长度为 \(N\) 的数列 \(A\) 和 \(B\)，其中 \(A_i\in [1,2N],B_i\in [1,2N]\) 或 \(B_i = -1\)。

此外，合并 \(A\) 和 \(B\) 后，除了 \(-1\) 之外的整数最多只出现一次。

请计算满足以下条件的 能被定义的 数列 \(a, b\) 的数量，对 \(998244353\) 取模：

• \(a_i = A_i\)

• \(\forall B_i\neq -1,b_i = B_i\)

\(2 \leq N \leq {\color{red}{10^6}},A_i\in [1,2N],B_i\in [1,2N]\) 或 \(B_i = -1\)。

保证 \(A,B\) 中的数两两不等。

题解

这题很关键的一点是 \(a\)​ 已经全部知道了。这种问题还是先来搞 判定。

---

考虑 \(s\cup t\) 中开头为 \(i\) 的恰好出现两次，分别在 \(s,t\) 中。于是 \(2i-1,2i\) 一个在 \(a\)，一个在 \(b\)​。

称 \(2i-1,2i\) 对应的 \(a,b\) 位置 \(x,y\) 为同一组。记 \(s_i, t_i\) 中间元素为 \(c_i\)​。

对于同一组，让其中 \(a\) 对应的 \(c_x\) 向 \(b\) 对应的 \(c_y\)​​​ 连 有向边，方向为 小的指向大的。

此时 \(a,b\) 合法等价于图无环，随便给 \(c\)​ 赋个拓扑序就有解了。

---

• 但是我们发现这样的 有向边 不好处理后续步骤。

来更好刻画方向：发现若 \(a_x=2i-1\) 是奇数，则 \(x\to y\)，否则 \(y\to x\)。

于是不妨把边建成 \(x\leftrightarrow y\) 的无向边。边的颜色为 \(a_y\bmod 2\)。

此时原来的图无环就等价于没有 同色环。

---

我们不妨对 \((a_i,b_i)\) 按 \(a\) 排序，若 \(a_i\not\in\{2i-1,2i\}\)​ 那么无解。

然后考虑对于有值的 \(b_i\)，此时连边已经确定了 \(\frac{b_i+1}{2}\leftrightarrow i\)，颜色设为 \(a_i\bmod 2\) 就行，一样的。

然后 \(b_i=-1\)​ 相当于有些链开头没连。然后其他已经连成一些环。

• 首先已经成的环无法再动了，判断下有无同色环，然后直接丢掉即可。

现在要把链串成环，求不存在同色环的方案数。

现在设有 \(x\) 个全 \(0\) 链，\(y\) 个全 \(1\) 链，\(z\) 个 \(01\) 混色链。

直接把链看成点，要串这 \(m=x+y+z\)​ 个点，不能有同色环。

钦定 \(k\) 个同色环，此时容斥系数是 \((-1)^{k}\)。

钦定 \(x\) 个全 \(0\) 选 \(p\) 个组成 \(q\) 个环，\(y\) 个全 \(1\) 选 \(r\) 个组成 \(s\) 个环。

然后剩下 \(m-p-q\) 个点任意串，方案数为 \((m-p-q)!\)。

再记一个 \(g_{i,j}\) 表示 \(i\) 个点串成 \(j\) 个环的方案数，则：

\[{\begin{aligned} ans&=\sum\limits_{0\le p\le x}\sum\limits_{0\le q\le y}\dbinom{x}{p}\dbinom{y}{q}(m-p-q)!\sum\limits_{0\le r\le p}\sum\limits_{0\le s\le q}(-1)^{r+s}g_{p,r}g_{q,s}\\ &=\sum\limits_{0\le p\le x}\sum\limits_{0\le q\le y}\dbinom{x}{p}\dbinom{y}{q}(m-p-q)!f_pf_q \end{aligned}} \\ f_n=\sum\limits_{i=0}^n (-1)^i g_{n,i} \]

\(f_n\) 即 \(1\sim n\) 所有排列的 \((-1)^{\text{置换环个数}}\) 的和。

这东西注意到经典双射，交换 \((p_1,p_2)\) 能使置换环个数 \(\pm 1\)。所以当 \(n\ge 2\) 时 \(f_n=0\)。

然后 \(f_0=1,f_1=-1\)。只需枚举 \(p\in [0,1],q\in [0,1]\)​ 即可。

求 \(x,y,z\) 用并查集多维护几个量即可。复杂度是高贵的线性！

\(\bf{record}\)

E (Gravity Sort)

题意

在一个从上到下排成一列的 \(2N\) 个格子中，每个格子都有一个编号，从 \(1\) 到 \(2N\)。每个格子里放着一个球。

在时刻 \(t=0\)，编号 \(i\) 的格子中球的重量为：若 \(i=1,2,\ldots,N\)，则为 \(m_i\)；若 \(i=N+1,N+2,\ldots,2N\)，则为 \(0\)。

• 保证 \((m_1, m_2, \ldots, m_N)\) 是 \(1\) 到 \(N\) 的一个排列。

在接下来的时间里，重球会下沉，轻球会上浮。具体来说，给定时刻 \(t=t_0\)，我们按照以下步骤确定时刻 \(t=t_0+1\) 的球位置：

1. 从 \(i:N\to 1\) 依次处理：

   • 如果球 \(i\) 在时刻 \(t=t_0+1\) 的位置已确定，则不进行操作。
   • 如果球 \(i\) 在时刻 \(t=t_0+1\) 的位置尚未确定：
     • 若其下方的格子存在于时刻 \(t=t_0\)，且该位置球的重量小于球 \(i\)，则交换并确定下两个位置。
     • 否则，保持球 \(i\) 在时刻 \(t=t_0+1\) 的位置不变。

2. 对于所有尚未确定位置的重量为 \(0\) 的球，保持其位置不变。

最终，在某一时刻，球将按由上到下轻重顺序排列，且此后位置不再变化。请计算实现这一状态所需的最小时刻。

\(1\le N\le 2\times 10^5\)

题解

为方便叙述，下文把原来 竖直的格子看成横着的序列。

---

下文称 \(i\) 球表示权值为 \(i\) 的球。先对操作进行初步分析：

发现这个过程在 不断消除逆序对，已经变成顺序对不会再换成逆序。

这启发我们：当所有重量 \(<i\) 的球 (包括所有 \(0\) 球) 都换到 \(i\) 球前面时，称 \(i\) 球达到 状态 A。

• \(i\) 球达到 状态 A 后，会一直保持 状态 A。

• 而当所有球达到 状态 A 时，即序列被排序了。

所以对于每个球我们只关心它到达到 状态 A 的时刻为 \(T_i\)。后续时刻并不关心。

---

发现不断有球跨过 \(n\to n+1\) 抵达右半边，并且前面带着一个 \(0\)，之后一段时间内 \((0i)\) 会一起向右移动。

设为 \(i\) 球从 \(n\to n+1\) 的时刻为 \(t_i\)。

于是我们把问题拆成两步：如何求 \(t_i\)；如何根据 \(t_i\) 算答案 \(ans\)。

如何算 \(ans\)

给出结论：\(\color{red}{ans=\max(t_i+i-1)}\)

证明

考虑从 \(t_i\) 带来 \(0\) 开始，到 \(T_i\) 达到 状态 A，这里 \(i\) 球要怎么动：

比如 \(x,y,z\) 在 \(i\) 之前跨中线，写出这样一个序列：

...(0i0z0y0x)->...

发现当 \(x\) 没有抵达 \(2n\) 位置时，这个整体向右移动。

...0i0z0y0x| <- 抵达 2n 位置

当抵达 \(2n\) 位置时，\(i\) 后面那些球开始 内部交换，xyz 内部交换，交换成 XYZ。

0i0XYZ|

到 \(i\) 后面只有紧贴 \(i\) 后面那个 \(0\) 的时候，\(i\) 将要加入内部交换了，考察之后 \(i\) 的移动方式：

当 XYZ 全部比 \(i\) 小的时候，\(i\) 可以一路平推，推到最后一个位置。

这启发我们：把 XYZ... 之中 \(<i\) 的看成 O，把 \(>i\) 的看成 I。

可以举例 0i0OOOIOOII 这样模拟一下。

注意到 \(i\) 和每个 I 是同时在做 $\to $ 操作，相向而行，把 O 往前换。

于是当 \(i\) 碰到一个 I 的时候，后面一定全是 I，没有 O，就抵达了状态 A！

所以我们得出结论：在 \([t_i,T_i]\) 这段时刻，\(i\) 球始终向右运动！

---

考虑 \(t=ans\) 这个时刻，一定有个数 \(x\) 没有达到 状态 A，才需要一次交换。

根据结论，\(x\) 球在 \(t_i\) 后 一直向右移动，直到 \(ans\) 时刻 第一次到达 位置 \(n+x\)，并达成 状态 A。

于是 \(ans=t_x+x-1\)。

---

显然有 \(ans\ge \max(t_i+i-1)\)，因为每个球 \(i\) 跨过终点后都至少要走 \(i-1\) 步到达 \(n+i\)。

由于上面证明了 \(ans\) 取到某个 \(t_x+x-1\)，就有 \(\color{red}{ans=\max(t_i+i-1)}\)。

如何求 \(t_i\)

接下来求 \(t_i\)，设 \(i\) 球初始位置为 \(p_i\)。

理想情况下 \(t_i=n-p_i+1\) 畅通无阻的到达。真实显然有 \(t_i\ge n-p_i+1\)。

并且任意两个 \(\vert t_i-t_j\vert >1\)，毕竟两个数不能紧挨着跨过 \(n\to n+1\)，分讨下大小随便说明。

由于考虑到每个球的时候只关心重量 $\ge $ 它的球，于是我们给出结论：

从 \(n\to 1\) 球确定 \(t_i\)，具体的：

\[\color{red}{t_i=\{x\ge n-p_i+1:\forall j>i,x\neq t_j-1,t_j,t_{j}+1\}_{\min}} \]

证明

引理：当时刻 \(t\ge 1\) 时，序列中不存在 \(x> y> z\ge 0\) 的下降子序列。

考虑 \(t-1\to t\) 这一步 \(y\) 是怎么来的，发现没法来。

下面我们给出 结论：取

\[\color{blue}{t'_i=\{x\ge n-p_i+1:\forall j>i,x\neq t_j-1,t_j,t_{j}+1\}_{\min}} \]

则当 \(i\) 球达到 \(t-x=t'_i-(n+1)\) 这条直线后，\(i\) 球之后始终向右走。

• 下图和原题样例图坐标轴反过来了，竖轴是时间，横轴是序列。

• 记 \(x\) 表示位置，\(t\) 表示时刻，如下图中坐标轴。

• 直线交 \(x\) 轴和交 \(t\) 轴的情况没有区别，这里随便画了一个。

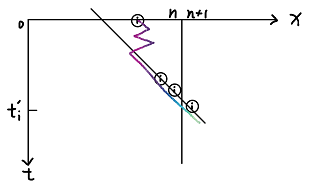
如上图，我们认为 \(i\) 的运动轨迹即是彩色的线。

考虑这个结论怎么推导出 \(t_i\) 的取值。

首先真实 \(t_i\ge t'_i\)，所以必定经过图中直线，并且之前在直线内部运动。

由于到达直线一直向右走，直到跨过中线。于是 \(t_i=t'_i\)。

接下来证明这个结论。

我们给出 更强结论，在 \(t-x=t'_i-(n+1)+\{-1,0,1\}\) 三条直线中，当 \(t\le t'_i\) 时，所有数 几乎全都 \(\le i\)。

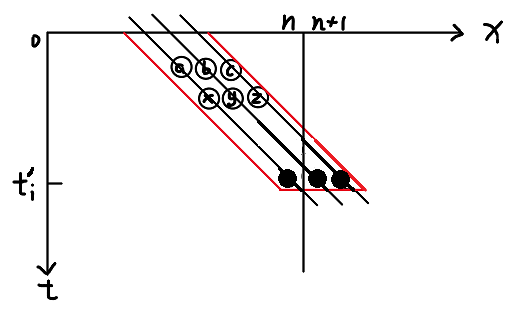
即上图红框部分 \(\le i\)。这里 \((a,b,c)\) 和 \((x,y,z)\) 对应相邻时刻。

首先 \(t'_i\) 时刻三个数（实心球位置）都 \(\le i\)。

• 否则 \(t'_i\) 就和某个 \(j>i\) 的 \(t_j\) 差不超过 \(1\)，矛盾。

我们由下至上归纳证明，考虑由 \(x,y,z\le i\) 推到 \(a,b,c\le i\)。

每个数只能左右移一步或者不动。

• \(c\) 显然怎么移都在 \(x,y,z\) 中，于是 \(c\le i\)。

• • \(b\) 不动或者 \(b\) 右移分别对应着 \(x,y\)。

  • 若 \(b>i\) 并且 \(b\) 左移了，那必然 \(a>b>i\) 换了 \(b\)。

    于是 \(x=a>i\)，矛盾。从而 \(b\le i\)。

• • \(a\) 右移对应 \(x\)。

  • 由于 \(b\le i\)，\(a\) 不可能不动。

  • 若 \(a\) 左移，并且 \(a>i\)。设 \(a\) 前一个数为 \(d\)。

    则 \(d>a>i\ge b\)，\((d,a,b)\) 就是长度为 \(3\) 的下降子序列。

  于是当 \(t\ge 1\) 时，\(a\le i\)。

更强结论在 \(t\ge 1\) 时刻恒成立。

当 \(t=0\) 时，\((d,a)\) 先交换了，\(c\le i\)，不影响最初在 \(b\) 位置上的 \(i\) 右移。这个数依然向右移。

于是并不影响始终向右的结论。

至此证明了恰好能取到 \(\color{red}{t_i=t'_i}\)。

如何维护

求 \(t_i\) 相当于动态删除，查询 \(\ge x\) 的最小值。显然可以使用 set 维护。

由于 \(t_i\) 的值域是 \([0,3n]\)，可以使用序列并查集维护。做到小常数 \(\mathcal{O}(n\log n)\)。

鲜花

• 这里特别感谢伟大的刘恒熙的指导！

• 感谢某不愿透露姓名的同学对第一部分证明的贡献。

很深刻的题，大家别看这题代码就几行很简单，但是思维其实 非常难，场上零个人过。

对两个形式极其简单的证明是这题 最精彩的部分，之前过这个题的选手少说九成九都不会完整证明。

我断断续续奋战了 两周，编写了目前第一篇题解，也是第一篇 有详细严格证明的题解。

AT 官方题解感觉很难绷，结论一笔带过，证明是一个字不提的，看着就有种假假的感觉。

最后还是依靠 lhx 的思路完成了这个题的证明。

并且我合理猜测 lhx 同我的 Q&A 是他现场想的证明，感叹国家队水平还是太牛了！

---

这题给出做法以及证明的过程太过艰难了，以我微薄的能力无法诠释如何想出此等做法，留给后人思考。

\(\bf{record}\)