2025 福建省队集训录

鲜花

天空没有极限 | 我的未来无边

于 2025/6/30~7/1

傍晚放学，骄阳在黄昏中无奈沉沦，悄然隐没于地平线。

六月的最后一天依旧以失败收场——足球赛上我纵横驰骋，却难逃压哨绝杀；$1+0$ 国际象棋中我占尽优势，却被拖入残局，终因时间耗尽而败。

我想，我的省集大概也难逃同样的命运吧。

恍然欲会周公，思绪悄拂初二那年盛夏。数学老师在试卷评语上写下眼高手低四字，带着几分讽刺。我却干脆利落地擦掉了眼和低两个字，只剩下鲜红的高手映入眼帘。

不过是没考班级第一罢了，这次没考好，那就下次拿满分回来。实力摆在那里，自然无惧风雨。

曾经迷茫，曾经自我怀疑，但在 OI 的征途中，我一次次证明：那些看似高不可攀的大佬并非我无法击败。

不该有天生不如人的怅惘，我唯一要做的，就是一次次爬起，再度出发，一次次向山巅发起冲击。

未虑胜先虑败，不应是我的风格，自信仍是我最大的底牌。

眼下，唯有竭尽全力打好每一场比赛。即便无法超越高手，至少也能昭示：我曾奋力攀登！

翌日清晨，风卷云舒，阳光淬炼着我炽热的决心。轻启省集第一页，心底已不留一丝彷徨。

2025/7/2

花絮：零个人在 OJ 上用自己头像，我是为数不多给自己头像丢脸的选手。

2025/7/4

花絮：失去姓氏。

2025/7/6

第一次有题没分的场，傻逼论文题写挂了！

诞生了新的实际 rk.1，chy 太超模了。

目标

上一次 $100$ $\color{green}{\checkmark\text{ on Day 1}}$
上一次 $200$ $\color{green}{\checkmark\text{ on Day 4}}$
过一题 $\color{green}{\checkmark\text{ on Day 3}}$
一次分数进省队线 $\color{green}{\checkmark\text{ on Day 1}}$
一次前十 $\color{green}{\checkmark\text{ on Day 3}}$
一次前五 $\color{green}{\checkmark\text{ on Day 4}\ ({\bf{rk.1}})}$

$\scr{Day}\ 1$

$90+85+16=191$，rk.13。

T1 (tree)

交互题，交互库自适应

给定 $h$，令 $n=2^h-1$，有一棵 $u\sim \lfloor u/2\rfloor$ 连边的满二叉树。

树上每个点有个点权 $f_i\ge 1$，$n$ 个点有个排列 $p_i$。

每次询问 u d，交互库会返回 $s(u,d)=\sum\limits_{dis(p_u,x)=d} f_x$，其中 $1\le u\le n,1\le d\le 10^9$，若不存在距离为 $d$ 的点则为 $0$。

最终只要求 $\sum\limits_{i=1}^n f_i$。记询问次数为 $Q$，问 $u$ 的次数为 $c_u$，令 $U=\max\limits_{u} c_u$。

要求做到 $\color{red}{Q\le 2n+3,U\le 4}$，特别的，$U\le 5$ 有 $90\text{pts}$。

$3\le h\le 15,1\le f_i\le 10^9$

$\bf{solution}$

设树根为 $rt$，其两个儿子为 $c_1,c_2$。

首先容易想到询问 $\sum s(u,1)$，对每个点的 $f$ 算贡献系数，则根的系数为 $2$，非根非叶子的系数为 $3$，叶子的系数为 $1$。

于是我们只需要知道 $f_{rt}$ 与叶子的权值和。

首先叶子权值和就是 $s(rt,h-1)$，我们只需要问出 $rt$。

根的权值就考虑一个容斥，有等式 $2f_{rt}=s(c_1,1)+s(c_2,1)-s(rt,2)$。

这里的 $s(c_1/c_2,1)$ 在最开头 $\sum s(u,1)$ 中记录，这里就减少两次。

怎么求根和其两个儿子呢？

根是唯一没有距离为 $h$ 的点的位置，根和其两个儿子没有距离为 $h+1$ 的点。

你问 $(*,h+1)$ 出根和其两个儿子形成的集合，然后对这三个点问出根，然后就按上面算答案即可。

优化：问了 $n-1$ 个点后，还没有全问出根和其儿子，那么最后一个点一定是，就不再问一次。其他也是类似优化。

次数卡卡能进 $2n+3$，但是根最坏会被问 $5$ 次。

考虑要减少一次根的询问。

由于在询问根的时候询问了 $s\left(c_{1/2},h\right)$，发现 $s\left(c_{1/2},h\right)$ 是 $c_{2/1}$ 子树内的叶子和！

于是 $s(c_1,h)+s(c_2,h)$ 就是叶子的点权和，就做完啦！

$\bf{code}$

#include<bits/stdc++.h>
#include "tree.h"
#define LL long long
#define fr(x) freopen(#x".in","r",stdin);freopen(#x".out","w",stdout);
using namespace std;
const int N=1<<15|5;
int n;LL a[4],I[N];
LL solve(int tid,int h)
{
    n=(1<<h)-1;vector<int>g;
    for(int i=1,x;i<n;i++) if(!ask(i,h+1)) g.push_back(i);
    if(g.size()!=3) g.push_back(n);
    for(int i=0;i<3;i++) a[i]=ask(g[i],h);
	for(int i=0;i<3;i++) if(!a[i]){swap(g[i],g.back());break;}
    LL S=2*(a[0]+a[1]+a[2]);int rt=g.back();
    for(int i=1;i<=n;i++) I[i]=ask(i,1),S+=I[i];
    S+=(I[g[0]]+I[g[1]]-ask(rt,2))/2;
    return S/3;
}

T2 (loong)

有 $n$ 个英雄，每个人有攻击力 $a_i$ 和防御力 $b_i$。保证所有 $a_i,b_i$ 互不相同。

称一个英雄集合 $S$ 是好的，当且仅当 $\forall i, j\in S,i\ne j:a_i\le b_j$。

$\forall k\in [1,n]$，求出 $S\sube \{1,2,\cdots,k\}$ 且 $S$ 是好的时最大的 $|S|$。

$1\le n\le 10^6,1\le a_i,b_i\le 2n$。

部分分：保证 $a_i>b_i$，保证 $a_i<b_i$。

$\bf{solution}$

容易注意到所有 $a_i>b_i$ 的对只能选一个。

考虑 $a_i<b_i$ 的部分分怎么做。注意到对于任意集合中的 $i\neq j$，都要有：$a_i\le b_j,a_j\le b_i$。

于是把 $[a_i,b_i]$ 看成区间，这个条件等价于两两有交！此时必定存在点 $x$ 使得集合中所有 $a_i\le x,b_i\ge x$。

于是这档分就线段树区间 $[a_i,b_i]$ 加，查询全局最大值就是当前答案。

结合上面俩，考虑能否在剩下只选 $a_i<b_i$ 的情况下再加入一个 $a_i > b_i$ 的下标。

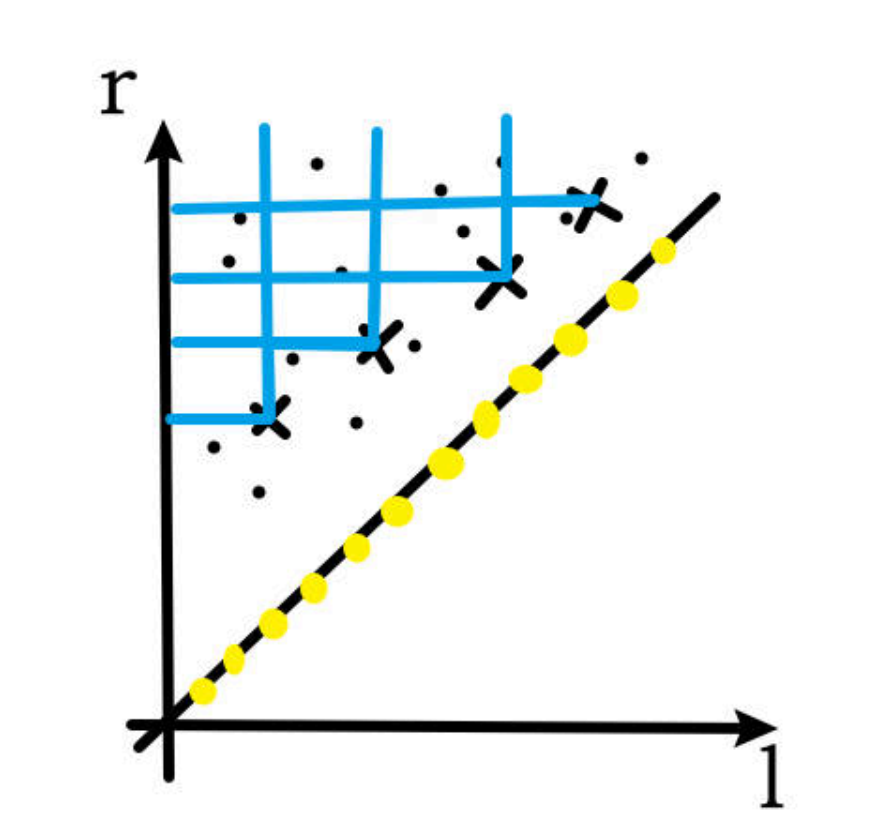
我们在二维平面上刻画该问题。

我们用 . 表示每个 $a_i<b_i$ 的 $(a_i,b_i)$，用 X 表示极短的 $a_i>b_i$ 的 $(b_i,a_i)$，用 O 表示横纵坐标相等的点。

设第 $i$ 个 X 左上方的点数为 $c_i$，第 $i$ 个 O 左上方的点数为 $d_i$，那么答案就是 $\max(\max c_i + 1, \max d_i)$。

加入 `X`

考虑把 X 的贡献记到 X 正下方的 O 上，如果某个时刻 X 不能贡献，则它就被 O 偏序了，于是一直不能贡献。

然后加入坐标为 $(b,a)$ 的 X 有贡献当且仅当所有点坐标都形如：$(\le b,\le b),(>a,>a),(\le b,>a)$

把 $x,y$ 坐标都丢进 set，只需判断是否 set 中所有 $>b$ 的都 $>a$ 即可。

set 容易用 BIT 替换，常数小一半。

加入 `.`

把应该被踢掉的 X 踢掉，然后在 O 上加上贡献即可。

把 X 加入线段树，然后每次查询是否有能删的即可。

线段树维护最大值，复杂度 $\mathcal {O} (n\log n)$。

$\bf{code}$

#include<bits/stdc++.h>
#define LL long long
#define P pair<int,int>
#define fi first
#define se second
#define ls w<<1
#define rs w<<1|1
#define lw l,m,ls
#define rw m+1,r,rs
#define fr(x) freopen(#x".in","r",stdin);freopen(#x".out","w",stdout);
using namespace std;
const int N=2e6+5,inf=1e9;
int id,n,lt[N<<2];
P mx[N<<2],c[N<<2];
inline void pu(int w){mx[w]=max(mx[ls],mx[rs]);}
inline void upd(int w,int x){mx[w].fi+=x,lt[w]+=x;}
inline void pd(int w){int &t=lt[w];if(t) upd(ls,t),upd(rs,t),t=0;}
void UPD(int L,int R,int l=1,int r=2*n,int w=1)
{
	if(L<=l&&r<=R) return upd(w,1);
	int m=(l+r)>>1;pd(w);
	if(L<=m) UPD(L,R,lw);
	if(m<R) UPD(L,R,rw);pu(w);
}
void add(int p,int x,int l=1,int r=2*n,int w=1)
{
	if(l==r) return mx[w].se+=x,void();
	int m=(l+r)>>1;pd(w);
	p<=m?add(p,x,lw):add(p,x,rw);pu(w);
}
void mdf(int x,int y,int l=1,int r=2*n,int w=1)
{
	if(l==r) return c[w]={y,x},void();
	int m=(l+r)>>1;x<=m?mdf(x,y,lw):mdf(x,y,rw);
	c[w]=max(c[ls],c[rs]);
}
P qry(int x,int y,int l=1,int r=2*n,int w=1)
{
	if(l>y||r<x||c[w].fi<y) return {0,0};
	if(x<=l&&r<=y) return c[w];
	int m=(l+r)>>1;return max(qry(x,y,lw),qry(x,y,rw));
}
struct BIT
{
	int a[N];
	inline void cl(){fill(a+1,a+1+2*n,inf);}
	inline void add(int w,int x){for(;w;w&=(w-1)) a[w]=min(a[w],x);}
	inline int ask(int w){int s=inf;for(;w<=2*n;w+=w&-w) s=min(s,a[w]);return s;}
}B;
int main()
{
	ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);cin>>id>>n;B.cl();
	for(int i=1,a,b;i<=n;i++)
	{
		cin>>a>>b;
		if(a<b)
		{
			UPD(a,b);B.add(a,a),B.add(b,b);
			while(1)
			{
				auto [u,v]=qry(1,b);
				if(u<b) break;add(v,-1),mdf(v,0);
			}
		}
		else
		{
			swap(a,b);int t=B.ask(a+1);
			if(t==inf||t>b) add(a,1),mdf(a,b);
		}
		cout<<mx[1].fi+mx[1].se<<"\n";
	}
	return 0;
}

T3 (lush)

给定一棵树，边有边权，边权可负。求 $1\sim n$ 的排列 $p$ 最小化权值 $\sum\limits_{i=1}^n \text{dis}(p_i,p_{i\bmod n+1})$。输出最小的权值。

$T\le 3$ 组多测，$1\le n\le 2\times 10^5,w_i\in [-10^3,10^3]$。

$\bf{solution}$

$\bf{code}$

$\scr{Day}\ 2$

$20+42+20=82$，rk.18。

T1 (trans)

给定一个长度为 $n$ 的序列 $a$，下标从 $1$ 开始，你可以进行以下操作若干次：

选择一个区间 $[l,r],\forall i\in \N,x\in \{0,1\},l+3i+x\le r$，将 $a_{l+3i+x}\gets a_{l+3i+x}+(-1)^x$。

问至少需要多少次操作，才能使 $a$ 序列的所有位置值均为 $0$。若无解，则输出 $-1$。

$T=30$ 组多测，$1\le n\le 3\times 10^4,|a_i|\le 10^{10}$。

$\bf{solution}$

存在线性规划做法，用于开拓视野。

考虑一个长度为 $n+2$ 的序列 $b$，其中 $b_i = a_i + a_{i-1} + a_{i-2}$。这里不妨假设对于 $i < 1$ 或 $i > n$ 的下标均有 $a_i = 0$。

然后观察一下操作，对于一次操作 $l, r:$

如果 $l \equiv r-1 \pmod{3}$，则记作操作 $1$，形象地说就是 $+1, -1$ 数量相等。

那么操作效果即为 $b_{r+2} \rightarrow b_{r+2} - 1,b_l \rightarrow b_l +1$，这里 $l, r+2$ 在 $\bmod 3$ 意义下相等。
如果 $l \equiv r \pmod{3}$，则记作操作 $2$，形象地说就是最多了一个 $+1$

那么有 $b_l \rightarrow b_l + 1, b_{r+1} \rightarrow b_{r+1} + 1, b_{r+2} \rightarrow b_{r+2} + 1$，不难发现 $r+1, r+2$ 相邻且 $l, r+1, r+2$ 在 $\bmod3$ 意义下两两不同。

显然只需要考虑这两种情况。

另外，操作 $2$ 会使序列中所有元素的减少，所以操作 $2$ 的代价已经是确定的。

考虑如果没有操作 $1$，该怎么做。

考虑从后往前贪心，假设现在做到了 $i$，也就是说 $b_j (j > i)$ 的位置都变成了 $0$。

如果 $b_i, b_{i-1}$ 均小于 $0$，那么我们做一次 $2$ 操作，然后另一个位置我们不确定，但我们能确定其 $\bmod 3$ 意义的值，我们可以先临时记录一下。

然后如果存在说 $b_i < 0, b_{i-1} = 0$，那么我们就把之前存放过的东西填充上去。不难发现这样做是最优的。

现在加入了 $1$ 操作，也就是说可以动态调整。

我们先考虑假如不需要做 $2$ 操作，如何做最优。

首先先不管最优不最优，考虑从后往前做，如果解，那么说明这一定是一个合法括号序列（任意一段前缀和大于等于 $0$）。最优的活链随便贪即可。

现在同时有了 $1, 2$ 操作，考虑什么时候 $1$ 操作可能会出问题，也就是说这一段前缀和小于 $0$ 了，我们在这里补一个 $2$ 操作。

我们考虑 $i = n+2 \rightarrow 1$ 扫描，其中扫描到 $i$ 时以后的 $b_i$ 均为 $0$。

开始分讨：

Case 1. $b_i = 0$。

不用理，继续往下做。

Case 2. $b_i > 0$

我们在这里不停地执行 $1$ 操作，把 $b_i$ 按下去，至于哪些位置会增加我们先不管，我们先记录一下做了该操作，显然会增加的位置和当前位置 $\bmod 3$ 意义下相等。

Case 3. $b_i < 0$

这里依次进行下面几步:

如果 $b_{i-1} < 0$，那么我们进行 $2$ 操作，这样会将 $b_{i-1}, b_i$ 同时增加 $1$, 重复直到 $\max(b_i, b_{i-1}) = 0$ 或者用完了 $2$ 操作次数为止。
如果 $b_i$ 仍然小于 $0$，考虑前面有些位置记录了要在 $\bmod 3 = x$ 的位置增加，那么我们把这些东西填充到这里，直到填满为止。
如果 $b_i$ 仍然小于 $0$，考虑现场挖坑，也就是将 $b_{i-1}$ 通过若干次减法操作变成 $b_i$，然后再执行 $2$ 操作，如果 $2$ 操作次数不够那么此题无解。

显然可以发现，这样做每一步都是最优的。

复杂度 $\mathcal{O}(Tn)$。

$\bf{code}$

#include<bits/stdc++.h>
#define LL long long
#define fr(x) freopen(#x".in","r",stdin);freopen(#x".out","w",stdout);
using namespace std;
const int N=3e4+7;
int T,n;LL a[N],b[N];
int main()
{
	fr(trans)
	ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);cin>>T>>n;
	while(T--)
	{
		LL s=0,mx=0;
		for(int i=1;i<=n;i++) cin>>a[i],s+=a[i],mx=max(mx,s);
		if(mx>0){cout<<"-1\n";continue;}fill(b+1,b+n+3,0);
		for(int i=1;i<=n+2;i++) for(int j=0;j<3&&j<i;j++) b[i]+=a[i-j];
		LL c=-s,ans=c,C[3]={0,0,0};
		for(int i=n+2;i;i--)
		{
			if(b[i]>=0) ans+=b[i],C[i%3]+=b[i];
			else
			{
				auto del=[&](LL x){c-=x,b[i]+=x,b[i-1]+=x;C[(i+1)%3]+=x;};
				if(b[i-1]<0) del(min({c,-b[i],-b[i-1]}));
				if(b[i]<0)
				{
					LL t=min(C[i%3],-b[i]);
					C[i%3]-=t,b[i]+=t;
				}
				if(b[i]<0) del(-b[i]);
			}
		}
		cout<<ans<<"\n";
	}
	return 0;
}

T2 (toxic)

Source：qoj 8592

交互题，交互库不自适应

有 $n=1000$ 种细菌，编号从 $0$ 到 $n-1$。有一些种类的细菌是有毒的，另一些是正常的。保证有毒和正常菌都存在。

现在我们想通过设计实验确定哪些种类的细菌是有毒的。

实验流程是把若干（不超过 $1000$）个细菌放到一行培养皿上，然后观察每轮存活细菌的数量。

注意：你可以在培养皿上放置多个同类的细菌。

每一轮中，如果某个细菌是正常的且它的左或右紧挨着有毒的细菌，那么这个正常的细菌就死亡了。

每一轮细菌死亡后，实验机器会自动把所有当前还存活的细菌按照之前的相对顺序紧挨着排列。

直到存活细菌的数量不发生变化，这一次实验就结束了。

请用尽可能少的实验次数来确定每种细菌是否有毒。

设次数为 $Q$，要求 $\color{red}{Q\le 21}$。

$\bf{solution}$

$\bf{code}$

#include<bits/stdc++.h>
#include "toxic.h"
#define LL long long
#define ask query_machine
#define vec vector<int>
#define fr(x) freopen(#x".in","r",stdin);freopen(#x".out","w",stdout);
using namespace std;
const int N=1005;
mt19937 rnd(time(0));
//query_machine
//answer_type
namespace NEW
{
	struct node{int c,k;};vector<node>C={
	{1,0},{2,0},{3,0},{4,0},{5,0},
	{2,1},{6,0},{7,0},{8,0},{9,0},
	{4,1},{10,0},{11,0},{2,2},{12,0},
	{13,0},{6,1},{14,0},{15,0},{16,0},
	{8,1},{17,0},{18,0},{4,2},{19,0},
	{20,0},{10,1},{21,0},{22,0},{23,0},
	{2,3},{24,0},{25,0},{12,1},{26,0},
	{27,0},{6,2},{28,0},{29,0},{14,1},
	{30,0},{31,0},{32,0},{33,0},{16,1},
	{34,0},{35,0},{8,2}};
}using namespace NEW;
void determine_type(int n)
{
    vector<char>ans(n,'@');vec p(n,0),res;
	iota(p.begin(),p.end(),0);shuffle(p.begin(),p.end(),rnd);

	int T;vec g(500,p[0]),G;
	for(int i=1;i<=499;i++) g.push_back(p[i]);res=ask(g);
	if(res.back()==g.size())
	{
		g=vec(500,p[500]);
		for(int i=501;i<n;i++) g.push_back(p[i]);
		res=ask(g);
		if(res.back()>500) T=p[500];
		else T=p[res.size()-499+500];
		bool o=ask({T,p[0]}).back()==2;
		for(int i=0;i<500;i++) ans[p[i]]="RT"[o];
		for(int i=500;i<n;i++) G.push_back(p[i]);
	}
	else
	{
		if(res.back()>500) T=p[0];
		else T=p[res.size()-499];
		for(int i=0;i<n;i++) G.push_back(i);
	}ans[T]='T';

	int B=C.size(),SZ=G.size();
	for(int i=0;i<SZ;i+=50)
	{
		g.clear();
		for(int j=23;j--;) g.push_back(G[i+B]);
		g.push_back(T);
		for(int j=0;j<B;j++)
		{
			auto [c,k]=C[j];
			for(int t=(1<<k);t--;)
			{
				for(int x=c;x--;) g.push_back(G[i+j]);
				g.push_back(T);
			}
		}
		for(int j=24;j--;) g.push_back(G[i+B+1]);

		res=ask(g);
		int sz=res.size(),t=g.size()-24-23;vec u(50,0);
		auto R24=[&]{
			ans[G[i+B+1]]='R';
			for(int i=0;i<24&&i<res.size();i++) res[i]-=(23-i);
		};
		auto T24=[&]{
			ans[G[i+B+1]]='T';
			for(int i=0;i<24&&i<res.size();i++) res[i]-=24;
		};
		auto R23=[&]{
			ans[G[i+B]]='R';
			for(int i=0;i<23&&i<res.size();i++) res[i]-=(22-i);
		};
		auto T23=[&]{
			ans[G[i+B]]='T';
			for(int i=0;i<23&&i<res.size();i++) res[i]-=23;
		};
		
		if(sz==24) R24(),(res[21]-res[22]==1)?R23():T23();
		else T24(),(sz==23)?R23():T23();
		
		while(sz<20) res.push_back(res.back()),sz++;
		res.insert(res.begin(),t);
		for(int j=0;j<B;j++)
		{
			auto [c,k]=C[j];
			if(c&1)
			{
				ans[G[i+j]]="TR"[(res[c/2]-res[c/2+1])&1];
				u[c/2]=ans[G[i+j]]=='R';
				continue;
			}c/=2;
			int d=(res[c-1]-res[c])-(res[c]-res[c+1])-u[c]-u[c-1];
			ans[G[i+j]]="TR"[d>>(k+1)&1];
		}
	}
	
	answer_type(ans);
}

T3 (second)

绵羊动物园即将召开全园动物代表大会，现任领导小老虎提出了关于修改动物园基本法的提案。

动物园有 $n$ 只动物，动物们的家构成了一棵树，初始第 $i$ 只动物在节点 $i$，其中小老虎的家是 $1$，也是大会召开的地方。

现在所有动物要赶往 $1$ 号节点，动物们非常喜欢一起行走，当一个动物走到 $u$ 号节点，它会等待所有会经过 $u$ 号节点的所有动物，直到它们都到达了 $u$ 号节点，然后一起向 $1$ 号节点走去。

每个节点 $u$ 都会有一个冰淇淋店，节点 $u$ 的冰淇淋售价为 $a_u$，质量为 $b_u$。

当两只动物第一次走到同一个节点 $u$ 时，它们会互相赠送给对方一个该节点售卖的冰淇淋。

对于每只动物，任意两个它收到的冰淇淋 $(i, j)$ 满足 $a_i < a_j \wedge b_i > b_j$，那么会给它产生 $1$ 的愉悦度。

现在想知道所有动物的愉悦度之和。

除此之外会有 $q$ 个独立事件：

1 u：第 $u$ 只动物消失了。

2 u v：第 $u$ 只和第 $v$ 只动物消失了 $(u \neq v)$

你需要对每个事件回答所有动物的愉悦度之和。

$1\le n,q\le 1.5\times 10^5,1\le a_i,b_i\le n$，保证所有 $a_i$ 互不相同，所有 $b_i$ 互不相同。

$\bf{solution}$

实在没有订正的欲望了，贺个题解

Sub1: q = 0

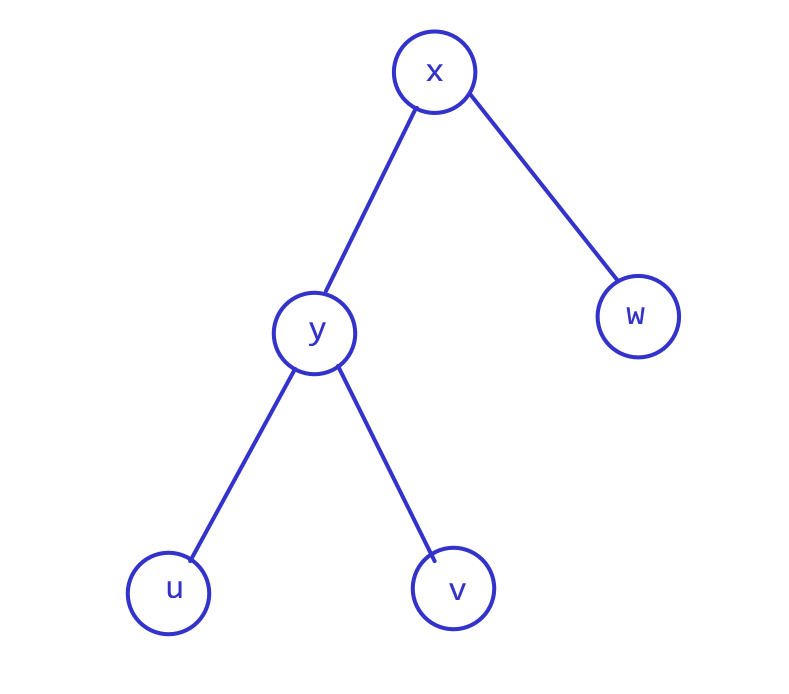
由题意得，$u$ 得到 $v$ 赠送的冰淇淋是在 $lca(u, v)$ 处购买的。对 $u$ 产生贡献的一对冰淇淋 $(u, v, w)$ 一定形如下图：

满足 $[a_y < a_x]\ne [b_y < b_x]$。这是一个二维偏序问题，为了方便理解，先忽略空间的限制，构建一个二维 BIT 来维护它。

设 $s(u)$ 表示 $u$ 子树的大小，$s_2(u)$ 表示 LCA 为 $u$ 的点对个数，$son_{a, b}$ 表示 $a$ 包含 $b$ 的那个儿子，对于每一对 $(x, y)$，$u, v$ 是等价的，产生了 $s_2(y)\times (s(x) - s(son_{x, y}))$ 的贡献。

从根开始 DFS，在 BIT 中维护当前节点 $u$ 的所有祖先的 $s(x) - s(son_{x, y})$，在 $y$ 处查询 $(a_y, b_y)$ 即可。

Sub2: op = 1

用总贡献减去消失动物的影响，有两种情况。

消失的动物在 $u/v$

记录 $s_3(u)$ 表示 $u$ 节点当作 $y$ 时所有 $x$ 的贡献，这个可以处理在 Sub1 的时候记录。

对于 $u$ 的每个 $y$，它的贡献是 $s_3(y)\times (s(y) - s(son_{y, u}))$，这个同样可以从根开始 DFS 处理。

消失的动物在 $w$

每个 $y$ 的贡献是 $s_2(y)$。

考虑 $y$ 对 $x$ 贡献，记 $gg(v)$ 表示 $v$ 的父亲 $u$ 子树中除去 $v$ 子树后所有 $y$ 对 $x = u$ 的贡献，$pp(u)$ 表示 $u$ 子树中所有 $y$ 对 $x = u$ 的贡献。

这两个东西可以通过差分 dfn 序列在二维 BIT 上维护。

算出 $gg$ 和 $pp$ 之后 DFS 到 $w$ 的时候处理询问。

Sub3

用 $op = 1$ 的做法减去两个点分别消失的贡献，再加回来两个点算重的情况，还是有两种。

消失的恰好在 $u, v$

贡献就是 $s_3(lca(u, v))$。

消失的一个是 $u/v$，一个是 $w$

$w$ 不用管它，每个询问拆成 $u\to lca(u, v)$ 和 $v\to lca(u, v)$ 两条链，对于每条链把询问通过差分挂到 $u$ 和 $x$ 查询，DFS 的时候在 BIT 中维护当前节点 $u$ 的所有祖先的 $s(x) - s(son_{x, y})$，和 $q = 0$ 的做法是类似的。

实现

上面的处理相当于给贡献和询问都增加了一个 dfn 维度，变成三维偏序用 cdq 分治处理。
卡了空间复杂度为 $O(n\log^2 n)$ 的树套树，但是允许离线的二维 BIT 的空间是可以做到 $O(n\log n)$ 的。

$\bf{code}$

$\scr{Day}\ 3$

$100+50+8=158$，rk.6。

T1 (sand)

你手上现有 $n+m$ 个石子，有 $n$ 个普通的石子和 $m$ 个特殊的石子。

这 $n+m$ 个石子共有 $c+1$ 种颜色，其中 $m$ 个特殊的石子的颜色为 $c+1$，其余石子的颜色为 $1 \sim c$ 中的一种。

已知第 $i$ 种颜色的石子有 $a_i$ 个，保证 $\sum\limits_{i=1}^{c} a_i = n$。

你将这些石子摆成一行，你决定观察你摆的石子的美观度。

为了方便观察，美观度由最左和最右边的石子决定，具体如下：

找到最左边的特殊的石子，记其为从左到右的第 $x$ 个石子。

考虑最右边的石子，若是普通石子，则找到其左边第一个颜色不同石子（可以是特殊石子），记其右边的石子数为 $y$。

序列的美观度定义如下：

如果最左边的石子是特殊的石子，则美观度为 $w_x$。

否则，记最右边的石子颜色为 $u$，则美观度为 $w_x \times v_{u,y}$。

其中 $w$ 和 $v$ 由题目给定。

现在你想知道，所有不同的石子序列，美观度之和是多少？

两个序列不同当且仅当至少有一个位置的石子颜色不同，答案对 $998244353$ 取模。

$1\le c\le n\le 2\times 10^5,1\le m\le 30,a_i\ge 1,\sum a_i=n,0\le w,v<998244353$

$\bf{solution}$

下面默认 $n<m$ 或 $m<0$ 时 $\dbinom{n}{m}=0$。记 $M=\prod\limits_{i=1}^n (a_i)!$

考虑 $w_x$ 的贡献，容易发现为：

\[\dfrac{n!}{M}\times \sum_{x=1}^{n+1} w_x\dbinom{n+m-x-1}{m-2} \]

注意特判 $m=1$，此时贡献为 $w_{n+1}$。

直接 $O(n)$ 算。

考虑 $w_x\times v_{u,y}$ 的贡献，发现答案为：

\[\sum_{x=1}^{n+1}\sum\limits_{u=1}^{c}\sum\limits_{y=1}^{a_u} w_x\times v_{u,y}\times \dbinom{n+m-x-y}{m-1}\times \dfrac{(n-y)!}{(a_u-y)!\prod_{i\neq u} (a_i)!} \\ \sum\limits_{u=1}^{c}\sum\limits_{y=1}^{a_u}v_{u,y} \times \dfrac{(n-y)!a_u!}{(a_u-y)!M}\sum_{x=1}^{n+1}w_x\dbinom{n+m-x-y}{m-1} \\ \sum\limits_{u=1}^{c}\sum\limits_{y=1}^{a_u}v_{u,y} \times \dfrac{(n-y)!a_u!}{(a_u-y)!M}\times F(y) \]

其中 $F(y)=\sum\limits_{i=1}^{n+1}w_x\dbinom{n+m-x-y}{m-1}$，于是我们只需求出 $F(1\sim n)$。

这东西首先随便 NTT 就能 $\mathcal{O}(n\log n)$ 求。

然后考虑经典递推：

\[\begin{aligned} F(y-1)&=\sum\limits_{i=1}^{n+1}w_x\dbinom{n+m-x-y+1}{m-1}\\ &=\sum\limits_{i=1}^{n+1}w_x\left(\dbinom{n+m-x-y}{m-1}+\dbinom{n+m-x-y}{m-2}\right)\\ \end{aligned} \]

于是你记 $F(y,e)=\sum\limits_{i=1}^{n+1}w_x\dbinom{n+m-x-y}{e}$，则 $F(y-1,e)=F(y,e)+F(y,e-1)$。

特判 $e=0$ 边界即可，复杂度 $\mathcal{O}(nm)$。

$\bf{code}$

#include<bits/stdc++.h>
#define LL long long
#define fr(x) freopen(#x".in","r",stdin);freopen(#x".out","w",stdout);
using namespace std;
const int N=2e5+105,mod=998244353;
int n,m,c,w[N],s[N],a[N],jc[N],inv[N],ml=1,ans,f[N][31];
vector<int>v[N];
inline int md(int x){return x>=mod?x-mod:x;}
inline void ad(int &x,int y){x+=y;(x>=mod)&&(x-=mod);}
inline int ksm(int x,int p){int s=1;for(;p;(p&1)&&(s=1ll*s*x%mod),x=1ll*x*x%mod,p>>=1);return s;}
inline int C(int n,int m){return n<m?0:1ll*jc[n]*inv[m]%mod*inv[n-m]%mod;}
inline void init(int M=n+m)
{
    for(int i=*jc=1;i<=M;i++) jc[i]=1ll*jc[i-1]*i%mod;
    inv[M]=ksm(jc[M],mod-2);for(int i=M;i;i--) inv[i-1]=1ll*inv[i]*i%mod;
}
inline void sol1()
{
    if(m==1) ans=w[n+1];
    else for(int x=1;x<=n+1;x++) ans=(ans+1ll*w[x]*C(n+m-x-1,m-2))%mod;
    ans=1ll*ans*jc[n]%mod*ml%mod;
}
int main()
{
    fr(sand)
    ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);cin>>n>>m>>c;
    for(int i=1;i<=n+1;i++) cin>>w[i],s[i]=md(s[i-1]+w[i]);
    for(int i=1;i<=c;i++) cin>>a[i],v[i].resize(a[i]+1);
    for(int i=1;i<=c;i++) for(int j=1;j<=a[i];j++) cin>>v[i][j];init();

    for(int i=1;i<=c;i++) ml=1ll*ml*inv[a[i]]%mod;sol1();
    
    for(int i=1;i<=c;i++) for(int j=a[i];j;j--) ad(v[i][j],mod-v[i][j-1]);
    int V=*max_element(a+1,a+1+c);

    for(int e=0;e<m;e++) for(int x=1;x<=n+1;x++)
		f[V][e]=(f[V][e]+1ll*w[x]*C(n+m-x-V,e))%mod;
    
    for(int y=V;y>1;y--)
    {
        f[y-1][0]=s[min(n+m-y+1,n+1)];
        for(int e=1;e<m;e++) f[y-1][e]=md(f[y][e]+f[y][e-1]);
    }
    for(int u=1;u<=c;u++) for(int y=1;y<=a[u];y++)
    {
        int T=1ll*v[u][y]*jc[n-y]%mod*inv[a[u]-y]%mod*jc[a[u]]%mod*ml%mod;
        ans=(ans+1ll*T*f[y][m-1])%mod;
    }
    cout<<ans<<"\n";
    return 0;
}

T2 (tree)

Source：qoj 5404

交互题，交互库不自适应。

出题人有一棵大小为 $N$ 的有根二叉树（每个点只有不超过两个儿子）。节点点编号为 $1 \sim N$。

注意你并不知道这一棵树的根节点，也不知道这一棵树的具体形态。你只知道树上的节点个数 $N$。

定义树上一个点集 $S$ 的虚树点集 $V = \{\text{LCA}(u, v) \mid u, v \in S\}$，其中 $\text{LCA}(x, y)$ 表示 $x, y$ 在树上的最近公共祖先（这里我们定义 $\text{LCA}(x, x) = x$）。

你想要知道这一棵树的结构，于是慷慨的出题人给了你一个交互库。这个交互库会回答你的若干次询问，每次询问你可以给定一些点的标号（不能重复），交互库会返回这些点构成点集的虚树点集的大小。

交互库的询问次数是有限的，你需要在有限的询问中确定这一棵树的形态。

当然，有可能出题人在耍你，那一棵二叉树无法通过任意的有限次询问问出树的结构。

这个时候你需要向交互库说明不可能通过这种询问方式确定树的形态。

记 $Q$ 为你的询问次数。

$1\le N\le 500,2\nmid n$，保证每个点不可能只有一个儿子，限制为 $\color{red}{Q\le 4500}$，50pts。

$500< N\le 1000$，限制为 $\color{red}{Q\le 10500}$，50pts。

$\bf{solution}$

对每次询问进行一些等价转化：给出一个点集，询问有多少个点，满足两个子树内都有给定点集的点。

先考虑子任务一 怎么做，保证每个非叶子节点都有两个儿子。

那么，询问全集删除一个点，就可以得知这个点是否是叶子。

考虑从叶子到根进行类似拓扑排序的过程。

问题变成对于一个点 $u$，已经确定了 $u$ 子树的点集，需要求出 $u$ 的父亲。

考虑删除 $u$ 子树内所有点，可以发现，剩下的点集中，只有 $u$ 的父亲恰有一个儿子。

也就是说，保留剩下的叶子，只有 $u$ 的父亲不会被虚树还原。

因此，可以在非叶子节点中二分，找到没被还原的点，就是 $u$ 的父亲。

询问次数 $O(n \log n)$。

接着考虑存在一度点的情况。

可以证明，如果一个一度点的儿子不是二度点，那么这两个点是不可区分的，因为仅包含两个点其中一个的所有询问结果是一样的。

考虑在子任务 $1$ 的做法上进行一些修改。

首先还是询问全集删除一个点，这样可以区分出二度点集（答案为 $n$）和零度一度点集，因为答案为 $n-1$。

然后询问零度一度点集删除一个点，有两种可能结果：

答案为 $n-1$，这是一个一度点，或者是叶子并且父亲是一度点。
答案为 $n-2$，这是个叶子。

先不考虑答案为 $n-1$ 的点，对剩下的点按照算法一找父亲，因为一度点对虚树无影响。

这可能会失败，说明我们没有找到所有叶子，说明存在叶子父亲是一度点，这种情况下无解。

否则，我们已经找到了所有叶子，那么答案为 $n-1$ 的点都是一度点，并且儿子不是叶子。

现在考虑确定每个一度点在哪条边上。

考虑询问 $u, v$，我们能知道 $u, v$ 是否是祖先后代关系。

考虑类似全局平衡二叉树的结构，对二叉树进行重链剖分，先用一次询问判断是否在重链上，如果是则直接在重链上二分，因为每个点都是二度点，所以可以通过询问轻儿子来二分。

否则和全局平衡二叉树一样，按照轻儿子子树大小进行二分，求出在哪个轻子树，递归去做。

询问次数 $O(n \log n)$，需要注意常数，本题次数比较死。

$\bf{code}$

#include<bits/stdc++.h>
#include "tree.h"
#define LL long long
#define Q Query
#define vec vector<int>
#define SZ(x) x.size()
#define all(x) x.begin(),x.end()
#define fr(x) freopen(#x".in","r",stdin);freopen(#x".out","w",stdout);
using namespace std;
// Report(Fa,i)
// Query(S)
mt19937 rnd(time(0));
const int N=1005;
int fa[N];bool o=1,v[N];
inline void del(vec &x,int y){x.erase(find(all(x),y));}
inline vec operator+(vec x,vec y){for(int i:y) x.push_back(i);return x;}
void sol(vec a,vec lf)
{
	if(!SZ(a)||!SZ(lf)) return;
	int n=SZ(a)+SZ(lf),C=0;
	static int c[N];vec A,LF;
	for(int i:lf) if(!fa[i])
	{
		vec A=a,t=lf;del(t,i);
		while(SZ(A)>1)
		{
			vec b[2];
			for(int j=0;j<SZ(A);j++) b[j&1].push_back(A[j]);
			swap(A,b[Q(b[1]+t)==n-1]);
		}
		fa[i]=A.back();c[fa[i]]++;C++;
	}
	if(!C) return o=0,void();
	for(int i:a) c[i]>=2?LF.push_back(i):A.push_back(i);
	for(int i:lf) if(c[fa[i]]<2) LF.push_back(i);
	sol(A,LF);
}
int sz[N],rt;vec E[N],w[N],wc[N];
void dfs(int x)
{
	sz[x]=1;int ms=0;
	for(int y:E[x]) dfs(y),sz[x]+=sz[y],(sz[y]>sz[ms])&&(ms=y);
	swap(w[x],w[ms]),swap(wc[x],wc[ms]);w[x].push_back(x);
	if(ms) wc[x].push_back(E[x][0]^E[x][1]^ms);
}
inline int get(int x)
{
	int p=rt;
	while(1)
	{
		auto &g=wc[p];
		int l=0,r=SZ(g)-1,m;
		if(Q({x,w[p].back()})==2)
		{
			while(l<r) m=(l+r)>>1,Q({x,g[m]})==2?r=m:l=m+1;
			return w[p][r];
		}
		while(l<r)
		{
			int S=0;for(int i=l;i<=r;i++) S+=sz[g[i]];
			for(int s=0,i=m=l,mx=-1e9;i<r;i++)
			{
				s+=sz[g[i]];int t=min(S-s,s);
				if(t>=mx) m=i,mx=t;
			}
			(Q({x,w[p][m+1]})==2)?l=m+1:r=m;
		}
		p=g[r];
	}
}
void Solve(int n)
{
	auto wr=[&](){for(int i=1;i<=n;i++) if(fa[i]) Report(fa[i],i);};
	vec d0,d1,d2,rs;
	for(int i=1;i<=n;i++)
	{
		vec g;
		for(int j=1;j<=n;j++) if(i!=j) g.push_back(j);
		if(Q(g)==n-1) rs.push_back(i);
		else d2.push_back(i);
	}
	if(n<=500&&(n&1)) return sol(d2,rs),wr();
	for(int i:rs)
	{
		vec g=rs;del(g,i);
		if(Q(g)==n-2) d0.push_back(i);
		else d1.push_back(i);
	}sol(d2,d0);
	if(!o||d0.empty()) return Report(-1,-1);int c=0;

	for(int i:d0+d2) fa[i]?E[fa[i]].push_back(i),c++:rt=i;
	if(c+1!=SZ(d0)+SZ(d2)) return Report(-1,-1);dfs(rt);
	for(int i:d0+d2) reverse(all(w[i])),reverse(all(wc[i]));

	for(int i:d1)
	{
		int p=get(i);
		if(v[p]) return Report(-1,-1);
		v[p]=1;fa[i]=fa[p],fa[p]=i;
	}
	for(int i=1;i<=n;i++) if(fa[i]) Report(fa[i],i);
}

T3 (future)

阿绫有 $2$ 个数组 $a, b$，一开始 $2$ 个数组为空数组。

阿绫会进行 $m$ 次操作，设当前数组长度为 $n$，操作有以下类型：

给定 $x, c, p, q, u, v$，分别在数组 $a, b$ 的第 $x$ 个数和第 $x+1$ 个数之间插入 $c$ 个数，$\forall 1 \le i \le c$，在 $a$ 中插入的第 $i$ 个数为 $pq^{i-1}$，在 $b$ 中插入的第 $i$ 个数为 $u+v(i-1)$。

给定 $l, r$，删除数组 $a, b$ 的区间 $[l, r]$。

给定 $l, r$，翻转数组 $a, b$ 的区间 $[l, r]$。

给定 $l, r$，询问 $\sum\limits_{i=l}^r a_i b_i$，答案对 $P = 10^9 + 7$ 取模。

给定 $l, r, u, v$，对数组 $b$ 的区间 $[l, r]$ 进行修改，对于 $l \le i \le r$，将 $b_i$ 修改为 $b_i + u + v(i-l)$。

$1\le m\le 3\times 10^5,0\le x\le n\le 10^9,1\le l\le r\le n,c\in [0,10^9],p,q\in [1,P-1],u,v\in [0,P-1]$

$\bf{solution}$

实在没有订正的欲望了，贺个题解

因为有插入删除和区间翻转操作，需要使用平衡树维护。

先考虑对于确定的数组 $a$ ,如何支持操作 $4, 5$, 也就是区间对 $b$ 加等差数列, 求区间 $a \times b$ 的和。

对平衡树的每个节点打懒标记，只需要对每个节点维护 $\sum\limits a_i$ 和 $\sum\limits i \times a_i$ 就可以 $\mathcal{O}(1)$ 打标记了。

现在需要解决序列长度 $n$ 很大的问题，考虑类似珂朵莉树，将每个插入的连续段缩成一个点维护，每次操作只会造成 $\mathcal{O}(1)$ 次分裂，总共的段数是 $\mathcal{O}(m)$。

那么现在的问题就是，对于一个等比数列, $1, q, q^2, \cdots, q^{t-1}$, 快速的求出 $\sum\limits_{i=1}^t q^{i-1}$ 和 $\sum\limits_{i=1}^t i q^{i-1}$, 下面介绍 2 种方法。

容易想到是用等比数列求和公式，可以求出 $\sum\limits_{i=1}^t q^{i-1} = \frac{q^t-1}{q-1} $。

同样的类似等比数列求和公式的推导，设 $\sum\limits_{i=1}^t iq^{i-1} = S$, 则 $qS - S = tq^t - \sum\limits_{i=1}^t q^{i-1}$, 即 $(q-1)S = tq^t - \frac{q^t-1}{q-1}$。

上述做法需要逆元，并且特判 $q = 1$。

还有一种不用求逆元的方法，适用于 $P$ 不是质数的情况。

类似快速幂的求法，考虑倍增求和，维护 $x_t = q^t$, $y_t = \sum\limits_{i=1}^t q^{i-1}$, $z_t = \sum\limits_{i=1}^t iq^{i-1}$。

那么可以得到 $x_{2t} = x_t^2, y_{2t} = y_t(1+x_t), z_{2t} = z_t(1+x_t) + ty_tx_t$。

对于区间翻转操作，直接再维护一个逆序信息即可 (或者部分信息可以直接计算得出)。

总共的分裂次数是 $\mathcal{O}(m)$ 的，设 $V$ 是值域，总时间复杂度为 $\mathcal{O}(m \log m + m \log V)$，空间复杂度 $\mathcal{O}(m)$。

$\bf{code}$

$\scr{Day}\ 4$

$40+100+100=240$，rk.1。

T1 (attack)

由于题面过长，请在查看 $\to$ 题面。

$\bf{solution}$

这东西不是人能想和写的，垃圾题目赶紧滚蛋！

$\bf{code}$

T2 (light)

Source：ARC139F

给定 $n,m$，有一个序列 $A_1,A_2,\cdots A_n\in [0, 2^m )$。

令 $F(A)$ 为所有子集异或和的最大值，即 $F(A)=\max\limits_{S\sube \{1,2,\cdots ,n\}}\left(\bigoplus\limits_{x\in S} A_x\right)$。

对于 $2^{nm}$ 种生成方式，求 $F(A)$ 的和模 $998244353$。

$1\le n\le 10^9,1\le m\le 2\times 10^6$。

$\bf{solution}$

懒得写了，请查看原题题解。

$\bf{code}$

#include<bits/stdc++.h>
#define LL long long
#define fr(x) freopen(#x".in","r",stdin);freopen(#x".out","w",stdout);
using namespace std;
const int N=2e6+5,mod=998244353,I2=(mod+1)>>1;
int n,m,a[N],jc[N],inv[N],p2[N],s[N];
inline int md(int x){return x>=mod?x-mod:x;}
inline int ksm(int x,int p){int s=1;for(;p;(p&1)&&(s=1ll*s*x%mod),x=1ll*x*x%mod,p>>=1);return s;}
inline int C(int n,int m){return n<m?0:1ll*jc[n]*inv[m]%mod*inv[n-m]%mod;}//q-binom
inline void init(int m)
{
    for(int i=*p2=1;i<=m;i++) p2[i]=md(p2[i-1]<<1);
    for(int i=1;i<=m;i++) a[i]=p2[i]-1;
    for(int i=*jc=1;i<=m;i++) jc[i]=1ll*jc[i-1]*a[i]%mod;
    inv[m]=ksm(jc[m],mod-2);for(int i=m;i;i--) inv[i-1]=1ll*inv[i]*a[i]%mod;
    for(int i=0;i<=m;i++) s[i]=ksm(2,n)-p2[i]+mod;
    for(int i=1;i<=m;i++) s[i]=1ll*s[i]*s[i-1]%mod;
}
int main()
{
    fr(light)
    ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);cin>>n>>m;
    init(m+1);int ans=0;
    for(int k=1;k<=min(n,m);k++)
    {
        int t=s[k-1],u=1ll*(p2[m+1]-p2[m-k]+mod-1)*C(m,k)%mod,v=(1ll*k*p2[k]+1)%mod*C(m,k+1)%mod;
        ans=(ans+1ll*t*(u-v+mod))%mod;
    }
    cout<<1ll*ans*I2%mod;
    return 0;
}

T3 (war)

Source：AGC063E

给定一棵 $n$ 个点的有根树，第 $i$ 个节点有父亲 $P_i$，每个节点上都有一个自然数 $A_i$。

你可以执行若干次以下操作：

选择一个 $i$ 满足 $2 \le i \le n$, $A_i > 0$，令 $A_i \rightarrow A_i - 1$, $A_{P_i} \rightarrow A_{P_i} + r$。

问有多少个不同的序列 $A$ 可以通过若干次操作得到，对 $998244353$ 取模。

$2\le n\le 300,0\le r,A_i\le 10^9$。

$\bf{solution}$

首先合法操作必然可以调成从下到上。

你先想一个暴力 dp：设 $f_{u,i}$ 表示 $u$ 子树向上进位 $i$ 的答案。

转移就下面给 $j$ 个上来，上面 $+jr$。

那么每次 $f'_{u,i+jr} \leftarrow f_{u,i} \times f_{v,j}$，然后对 $f_u$ 做后缀和。

先考虑根节点上的 $f$，用生成函数 $f_u$ 刻画：那么我们要求的就是所有方案中 $a_u+r \sum j_v$ 的值之和。

那么分拆下去我们要知道 $\sum\limits_j jf_{v,j}$，进一步要知道 $\sum\limits_j j^2 f_{w,j}$，其中 $P_w = v$。

这祺发我们上狄利克雷生成函数：设 $F_{u,k} = \sum f_{u,i}i^k$，那么考虑转移：

\[\begin{aligned} F'_{u,k} &= \sum_i f'_{u,i}i^k \\ &= \sum_{i,j} (i+jr)^k f_{u,i}f_{v,j} \\ &= \sum_{p=0}^k\sum\limits_{i} \binom{k}{p} f_{u,i}i^p \sum_j f_{v,j}j^{k-p}r^{k-p} \\ &= \sum_{p=0}^k \binom{k}{p} r^{k-p} F_{u,p}F_{v,k-p} \end{aligned} \]

这时候难点在于还要对 $f$ 后缀和，然后计算出之后的 $F$。

\[F'_{u,k}=\sum\limits_{i}i^k\sum\limits_{j\ge i} f_{u,j}=\sum\limits_{j} f_{u,j}\sum\limits_{i=1}^{j} i^k=\sum\limits_{j} f_{u,j}S(j,k) \\ S(n,m)=\sum\limits_{i=1}^n i^m \]

考虑经典自然数幂和转多项式，设伯努利数为 $B_n$。

有：$B_0=1,\sum\limits_{i=0}^n\dbinom{t+1}{i}B_i=0$。

则：

\[S(n,m)=\dfrac{1}{m+1}\sum\limits_{i=0}^m \dbinom{m+1}{i} B_i n^{t+1-i} \\ {\bf{let}}:S(n,m)=\sum\limits_{i=0}^{m+1}A(m,i)n^i \]

就有：

\[F'_{u,k}=\sum\limits_{j} f_{u,j}\sum\limits_{i=0}^{k+1}A(k,i)j^i=\sum\limits_{i=0}^{k+1} A(k,i) F_{u,i} \]

直接暴力算即可。复杂度 $\mathcal{O}(n^3)$。

$\bf{code}$

#include<bits/stdc++.h>
#define LL long long
#define fr(x) freopen(#x".in","r",stdin);freopen(#x".out","w",stdout);
using namespace std;
const int N=305,mod=998244353;
int n,r,a[N],C[N][N],S[N][N],f[N][N],g[N];
basic_string<int>E[N];
inline int md(int x){return x>=mod?x-mod:x;}
inline int ksm(int x,int p){int s=1;for(;p;(p&1)&&(s=1ll*s*x%mod),x=1ll*x*x%mod,p>>=1);return s;}
void dfs(int x,int d)
{
	for(int i=0;i<=d;i++) f[x][i]=ksm(a[x],i);
	for(int y:E[x])
	{
		dfs(y,d+1);memset(g,0,(n+1)<<2);
		for(int k=0;k<=d;k++) for(int p=0,pw=1;p<=k;p++,pw=1ll*pw*r%mod)
			g[k]=(g[k]+1ll*C[k][p]*pw%mod*f[x][k-p]%mod*f[y][p])%mod;
		memcpy(f[x],g,(n+1)<<2);
	}
	if(d^1)
	{
		memset(g,0,(n+1)<<2);
		for(int i=0;i<d;i++) for(int j=0;j<=i+1;j++)
			g[i]=(g[i]+1ll*f[x][j]*S[i][j])%mod;
		memcpy(f[x],g,(n+1)<<2);
	}//用系数做"前缀和"
}
int main()
{
	scanf("%d",&n);
	for(int i=2,x;i<=n;i++) scanf("%d",&x),E[x]+=i;
	scanf("%d",&r);
	for(int i=1;i<=n;i++) scanf("%d",&a[i]);
	for(int i=*C[0]=1;i<=n+1;i++) for(int j=*C[i]=1;j<=i;j++)
		C[i][j]=md(C[i-1][j]+C[i-1][j-1]);
	S[0][1]=1;
	for(int i=1;i<=n;i++)
	{
		for(int j=1;j<=i+1;j++) S[i][j]=C[i+1][j];
		for(int j=0;j<i;j++) for(int k=0;k<=j+1;k++) 
			S[i][k]=(S[i][k]+1ll*(mod-S[j][k])*C[i+1][j])%mod;
		for(int j=0,I=ksm(i+1,mod-2);j<=i+1;j++) S[i][j]=1ll*S[i][j]*I%mod;
	}S[0][0]++;//预处理自然数幂和的系数，和题解说的完全不一致，是另一种方法
	return dfs(1,1),cout<<f[1][0],0;
}

$\scr{Day}\ 5$

$100+25+24=149$，rk.15。

T1 (plan)

Source：P12558

过于简单不单独写题面和题解。

$\bf{solution}$

T2 (trans)

弱化版 Source：qoj 10305

请注意两题循环位移操作不一致。

给定一个 $n \times n$ 的 bool 矩阵 $B$，你需要对其进行转置。

你可以使用 $10^5 + 1$ 个长度为 $n$ 的辅助 bool 数组 $A_0 \sim A_{10^5}$，其中 $A_0 \sim A_{n-1}$ 初值为 $B_0 \sim B_{n-1}$，剩余数组的初值全为 $0$。

你可以调用以下操作：

AND x y z：将 $A_x$ 赋值为 $A_y \& A_z$，你需要保证 $0 \le x, y, z \le 10^5$。

OR x y z：将 $A_x$ 赋值为 $A_y \mid A_z$，你需要保证 $0 \le x, y, z \le 10^5$。

XOR x y z：将 $A_x$ 赋值为 $A_y \bigoplus A_z$，你需要保证 $0 \le x, y, z \le 10^5$。

SH x y z：将 $A_x$ 赋值为 $A_y$ 循环左移 $z$ 位，即 $A_{x,i}$ 最终的值为 $A_{y,(i-z) \bmod n}$，你需要保证 $0 \le x, y \le 10^5,0 \le z < n$。

SET x y z：将 $A_{x,y}$ 赋值为 $z$，你需要保证 $0 \le x \le 10^5,0 \le y < n,z \in \{0,1\}$。

你需要在尽可能少的操作次数内使得对于所有矩阵 $B$，在经过你进行的操作后，对于 $0 \le i, j < n$ 都有 $A_{i,j} = B_{j,i}$。

保证 $n=2^k,n\le 2048$，要求操作次数 $\color{red}{m\le 52000}$，构造符合条件的任意一个解即可。

$\bf{solution}$

$\bf{code}$

#include<bits/stdc++.h>
#define LL long long
#define fr(x) freopen(#x".in","r",stdin);freopen(#x".out","w",stdout);
using namespace std;
const int N=2051;
int n,m=2049,id[15][N];
struct node{string S;int x,y,z;};vector<node>g;
inline void add(string S,int x,int y,int z){g.push_back({S,x,y,z});}
inline void wr()
{
    cout<<g.size()<<"\n";
    for(auto [S,x,y,z]:g)
        cout<<S<<" "<<x<<" "<<y<<" "<<z<<"\n";
}
int main()
{
	ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);cin>>n;
	for(int k=1,i=0;k<n;k<<=1,i++)
	{
		id[i][0]=++m;
		add("SET",m,k,1);
		for(int j=1;j<=n/2;j<<=1) if(j^k)
			add("SH",2049,m,j),add("OR",m,m,2049);
		for(int j=1;j<k;j++) add("SH",id[i][j]=++m,id[i][0],j);
	}
	for(int i=1;i<n;i++) add("SH",i,i,i);
	for(int k=1,i=0;k<=n/2;k<<=1,i++)
		for(int j=0;j<n;j+=2*k) for(int t=j;t<j+k;t++)
		{
			add("XOR",++m,t,t+k);
			add("AND",m,m,id[i][t-j]);
			add("XOR",t,t,m);
			add("XOR",t+k,t+k,m);
		}
	for(int i=1;i<n;i++) add("SH",i,i,n-i);
	return wr(),0;
}

T3 (divisors)

Source：qoj 8416

交互题，交互库不自适应

Soyo 有一个隐藏的整数 $x$。Anon 知道 $N,C,T$ 三个数。

Anon 每次可以向 Soyo 询问一个非负整数 $y\le C$，Soyo 会回答 $x+y$ 的正因数个数。$x$ 是 Soyo 事先选定的，不会随着你的询问而变化。

Anon 知道 $x$ 是在 $[1,N]$ 中的整数，需要在若干次询问后求出 $x$ 的精确值。更准确地说，她需要在 $Q$ 次询问内求出 $T$ 个 $x$ 的值。

你需要帮助 Anon 完成这个任务。

有 $T=10$ 组多测，你要在使答案正确的情况下满足：$\color{red}{\sum Q\le 72\cdot T}$。

$1\le N\le 10^{14},C=10^{17}$

$\bf{solution}$

记 $d(n)$ 表示因数个数，$p^k\mid \mid n\Leftrightarrow p^k\mid n,p^{k+1}\nmid n$。

这个题你想数论性质就死啦！因为 $d(x+y)$ 根本没有任何可以利用的性质。

一个经典套路是想尽办法 CRT，又是见过好多次忘记啦！

这种题无论长啥样都要想充分久的二进制分解！

申明一个结论：$2^k\mid \mid n\Rightarrow k+1\mid d(n)$。

初始我们知道答案 $\bmod 2^0=0$，最终要求答案 $\bmod 2^{60}$ 或其他够大的结果。

然后 $k\to k+1$ 考虑填最高位。

如果我们已经求出答案 $\text{mod } 2^k$ 的值，如何拓展到 $\text{mod } 2^{k+1}$ 呢？

考虑先把 $x$ 补到 $2^k \cdot x_0$ ，我们只需要想办法找到一个 $2^k \cdot y_0$ 使得 $(x_0+y_0) \equiv 2 \pmod{4}$ 即可。

那么 $2^{k+1}\mid\mid 2^k(x_0+y_0)$，于是 $k+2\mid d(2^k(x_0+y_0))$，判一下即可。

但是考虑到即使存在 $2^{k+1}$ 因子，例如有 $3^{k+1}$ 这样。

返回值里的 $k+2$ 也可能会被别的质因数凑出来。

不过这个概率很小，而且也扩展不出很多步，直接搜所有的情况即可。

显然的卡常方式是对询问记忆化搜索。

另一个有效卡常的方式是在快要搜到底的时候枚举所有数看是否符合情况（我代码里没加）。

随便卡卡足以通过此题，$720$ 还是很充裕的。

$\bf{code}$

#include<bits/stdc++.h>
#include "divisors.h"
#define LL long long
#define fr(x) freopen(#x".in","r",stdin);freopen(#x".out","w",stdout);
using namespace std;
LL TT,U,q,c,ans=-1;
map<LL,LL>mp;
inline LL A(LL x){
	if(!mp.count(x)) return mp[x]=Ask(x);
	return mp[x];
}
bool dfs(LL d,int t)
{
	LL p=1ll<<t;if(p>U) return ans=d,1;
	LL ad=p-d;
	if(A(ad)%(t+1)==0&&dfs(d,t+1)) return 1;
	if(A(ad+p)%(t+1)==0&&dfs(d+p,t+1)) return 1;
	return 0;
}
int main()
{
    TT=GetT(),q=GetQ(),c=GetC(),U=GetN();
	while(TT--) mp.clear(),dfs(0,0),Answer(ans);
    return 0;
}

$\scr{Day}\ 6$

$60+100+0=160$，rk.9。

T1 (sort)

Source：qoj 4228

给定两个正整数 $n, m$，考虑如下的随机过程：

随机生成一个每个数都在 $[1, m]$ 且互不相同的整数序列 $[a_1, a_2, \dots, a_n]$，并将其升序排序。

求出 $a_i$ 的差分数组 $b_1, b_2, \dots, b_n$，即 $[a_1, a_2 - a_1, \dots, a_n - a_{n-1}]$。并将其升序排序。

求出 $b_i$ 的前缀和数组 $c_1, c_2, \dots, c_n$，即 $[b_1, b_1 + b_2, \dots, \sum b_i]$。显然 $c_i$ 是已经按升序排序的。

你需要对 $\forall 1 \le i \le n$，求出 $c_i$ 的期望。

答案对 $998244353$ 取模。

$1\le n\le 5000,n\le m\le 10^{6}$

$\bf{solution}$

给出 std 做法，是用 $\min-\max$ 容斥推的。

$\bf{code}$

#include<bits/stdc++.h>
#define LL long long
#define fr(x) freopen(#x".in","r",stdin);freopen(#x".out","w",stdout);
using namespace std;
const int N=1e6+5,M=5005,mod=998244353;
int n,m,jc[N],inv[N],f[M],g[M];
inline int md(int x){return x>=mod?x-mod:x;}
inline void ad(int &x,int y){x+=y;(x>=mod)&&(x-=mod);}
inline int ksm(int x,int p){int s=1;for(;p;(p&1)&&(s=1ll*s*x%mod),x=1ll*x*x%mod,p>>=1);return s;}
inline int C(int n,int m){return n<m?0:1ll*jc[n]*inv[m]%mod*inv[n-m]%mod;}
int main()
{
    fr(sort)
    ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);cin>>n>>m;
    for(int i=*jc=1;i<=m;i++) jc[i]=1ll*jc[i-1]*i%mod;
    inv[m]=ksm(jc[m],mod-2);for(int i=m;i;i--) inv[i-1]=1ll*inv[i]*i%mod;
	for(int i=1;i<=n;i++) for(int j=1;i*j<=m;j++)
		g[i]=(g[i]+1ll*C(n,i)*C(m-i*(j-1),n))%mod;
	for(int i=1;i<=n;i++) for(int k=i;k<=n;k++)
		f[i]=(f[i]+1ll*C(k,i)*(((k^i)&1)?mod-g[k]:g[k]))%mod;
	int I=ksm(C(m,n),mod-2);
	for(int i=n;i;i--) ad(f[i],f[i+1]);
	for(int i=n;i;i--) ad(f[i],f[i+1]),cout<<1ll*I*f[i]%mod<<"\n";
    return 0;
}

T2 (path)

Source：「核桃 NOI 组周赛 57」游乐园

游乐园里要添加一个闯关游戏。

游戏区域是一个 $n \times m$ 网格图。从 $(i, j)$ 到 $(i, j + 1)$ 的单向边预期需要时间 $r_{i,j}$，从 $(i, j)$ 到 $(i + 1, j)$ 的双向边预期需要时间 $c_{i,j}$。

游客需要从起点冲到最后一列。设计师想知道在哪里设置起点体验感最佳。

你需要告诉他如果在第 $i$ 行第一列 $(i, 1)$ 设置起点，到最后一列所有点 $(j, m)$ 的最短时间总和是多少。

形式化题面：对于每个 $i$，输出 $\sum\limits_{j=1}^n \mathrm{dis}(i, 1, j, m)$。其中 $\mathrm{dis}(x_1, y_1, x_2, y_2)$ 表示从 $(x_1, y_1)$ 到 $(x_2, y_2)$ 的最短路。

$1\le n\times m\le 2\times 10^5,r,c\in [1,10^6]$

$\bf{solution}$

$\bf{code}$

#include<bits/stdc++.h>
#define LL long long
#define fi first
#define se second
#define vec vector<int>
#define fr(x) freopen(#x".in","r",stdin);freopen(#x".out","w",stdout);
using namespace std;
const int N=2e5+5;const LL inf=1e18;
int n,m;LL ans[N];
vector<vec>r,c;
struct DSU
{
    vector<int>fa;
    inline void cl(int n){fa.resize(n);iota(fa.begin(),fa.end(),0);}
    inline int gf(int x){return x==fa[x]?x:fa[x]=gf(fa[x]);}
    inline void hb(int x,int y){x=gf(x),y=gf(y);if(x^y) fa[y]=x;}
};
struct G
{
    int n;vec a;
    struct E{int u,v;LL w;};
    vector<E>e;vector<LL>d;
    vector<pair<int,LL>>c;
    inline auto operator[](int x){return d[x];}
    inline void add(int u,int v,LL w){e.push_back({u,v,w});}
    inline void init(int s)
    {
        d=vector<LL>(n,inf);
        for(int i=0;i<n;i++) if(a[i]==s) d[i]=0;
        for(auto [u,v,w]:e) d[v]=min(d[v],d[u]+w);
    }
    inline LL get()
    {
        LL s=0;
        for(int i=0;i<n;i++) s+=d[i]*c[i].fi+c[i].se;
        return s;
    }
    inline friend G operator+(G &g1,G &g2)
    {
        DSU D;D.cl(g1.n);
        for(auto [u,v,w]:g1.e)
            if(D.fa[v]==v&&g1[u]+w==g1[v]&&g2[u]+w==g2[v])
            {
                auto [p,q]=g1.c[v];u=D.gf(u),D.hb(u,v);
                g1.c[u].fi+=p,g1.c[u].se+=p*(g1[v]-g1[u])+q;
            }
        G g;g.n=0;
        vector<int>id(g1.n,-1);
        for(int i=0;i<g1.n;i++) if(D.fa[i]==i)
            id[i]=g.n++,g.c.push_back(g1.c[i]),g.a.push_back(g1.a[i]);
        for(auto [u,v,w]:g1.e) if(D.fa[v]==v)
            g.add(id[D.gf(u)],id[v],w+g1[u]-g1[D.gf(u)]);
        return g;
    }
};
void sol(int l,int r,G g)
{
    if(l==r) return g.init(l),ans[l]=g.get(),void();
    G _g=g;g.init(l),_g.init(r);g=g+_g;
    int m=(l+r)>>1;sol(l,m,g),sol(m+1,r,g);
}
int main()
{
    fr(path)
    ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);cin>>n>>m;
    r.resize(n+1),c.resize(n+1);
    for(int i=1;i<=n;i++) r[i].resize(m),c[i].resize(m+1);
    for(int i=1;i<=n;i++) for(int j=1;j<m;j++) cin>>r[i][j];
    for(int i=1;i<n;i++) for(int j=1;j<=m;j++) cin>>c[i][j];
    auto W=[&](int i,int j){return (j-1)*n+i-1;};
    G g;g.n=n*m;
    for(int j=1;j<=m;j++)
    {
        if(j>1) for(int i=1;i<=n;i++) g.add(W(i,j-1),W(i,j),r[i][j-1]);
        for(int i=1;i<n;i++) g.add(W(i,j),W(i+1,j),c[i][j]);
        for(int i=n;i>1;i--) g.add(W(i,j),W(i-1,j),c[i-1][j]);
    }g.c.resize(n*m);g.a.resize(n*m);
    for(int i=1;i<=n;i++) g.c[W(i,m)]={1,0},g.a[W(i,1)]=i;
    sol(1,n,g);for(int i=1;i<=n;i++) cout<<ans[i]<<"\n";
    return 0;
}

T3 (count)

考虑 $\bmod 2$ 意义下的多项式乘法 $p(x)q(x) =f(x)$，则 $p(x)$ 称为 $f(x)$ 的因式。

给定 $\bmod 2$ 意义下的多项式 $f(x)$，你需要求出它有多少个因式。

由于答案可能很大，你只需输出答案对 $998244353$ 取模的结果即可。

$1\le n\le 2000$

$\bf{solution}$

前面忘了，比 std 快 $8$ 倍，后面忘了。

论文：Berlekamp 算法求 $\mathbb{F}_p$ 的因式分解，这题 $p=2$。

默认你们会了所有 bitset 做多项式运算以便 $/w$。

这个题你肯定是要做到 $\mathcal{O}(\frac{n^3}{w})$ 级别的。

有的做法理论能分析到 $\mathcal{O}(\frac{n^3}{w})$，但是注意到你 bitset 只能定长，于是有一些需要均摊的运算复杂度肯能会炸，于是需要你规避这些东西。

设现在要分解 $f$，先让 $f$ 变得无平方因子。

考虑经典结论：$A^2\mid f{\color{blue}{\,\Leftrightarrow\,}} A\mid f,A\mid f'{\color{blue}{\,\Leftrightarrow\,}} A\mid \gcd(f,f')$。

于是若 $f$ 有平方因子，设 $f=A^2B$，其中 $B$ 无平方因子。

我们考虑 $f'=A^2B'+2AA'B^2=A^2B'$，并且。

于是取 $\gcd(f,f')=A^2$ 即可分解出平方因子，然后递归下去即可。

于是现在考虑无平方因子的时候怎么分解。设现在要分解 $f$，$\deg f=n$。

考虑若有 $g^2\equiv g\pmod f$，并且 $g\ne 0,g\ne 1$：

那么 $f\mid g(g-1)\Rightarrow f=\gcd(f,g)\times \gcd(f,g-1)$，因为 $(g,g-1)=1$。

递归两个 $\gcd$ 部分即可。

考虑 $g^2\equiv g\pmod f$ 是一个 $n$ 元线性方程组。

具体的：设 $g=\sum\limits _{i=0}^{n-1} v_ix^i,\vec {v}=[v_0,v_1,\cdots ,v_{n-1}]$。

并且我们有一个矩阵 $Q$，满足第 $i$ 列为 $x^{2i}\bmod f$ 对应的系数，即满足 $Q_{j,i}=[x^j](x^{2i}\bmod f)$ 的矩阵。

那么 $g^2\bmod f=Q\vec v$，于是 $g^2\equiv g\pmod f\Leftrightarrow (Q-I)\vec v=0$。

这时 std 做法是每次找到一个解 $\vec{v}$，然后递归 $\gcd(f,g),\gcd(f,g-1)$。

这样复杂度不是特别对，因为理论递归 $n$ 层，然后你每次是 $\mathcal{O}(\frac{n^3}{w})$，所以理论会 $\mathcal{O}(\frac{n^4}{w})$。

但是这东西根本跑不满，所以随便过，不过比我下面做法慢 $8$ 倍！

但是这个题只要求因子个数，并非分解因式。

上面做法结结实实地分解因式了，所以会比较复杂。

我们有一些聪明的做法：

设 $D=Q-I$，定义 $\mathop{\text{rk}} $ 表示矩阵的秩，$\dim$ 表示一个空间的维度数。

首先 $D\vec v=0$ 的解 $\vec v$ 构成 $D$ 的零空间 $\text{Null}$，并且 $\mathop{\text{rk}} D+\dim {\text{Null}}=n$。

此时我们有结论：$f$ 恰好能分解为 $\dim \text{Null}$ 个不可约多项式乘积！

于是我们 $\mathcal{O}(\frac{n^3}{w})$ 高斯消元求出 $\mathop{\text{rk}} D$ 就能知道 $f$ 的分解个数。

其实这件事也容易通俗理解：$k$ 个基元素恰能分解 $k$ 次 $f$ 嘛！

证明可以自行搜索资料或询问 AI。

于是假设你知道了 $f=(A_1)^1(A_2)^2\cdots (A_t)^t$，并且 $A_1\sim A_t$ 都无平方因子。

那么我们用上面结论，分别求一下 $A_1\sim A_t$ 的分解个数，就能知道 $f$ 的分解个数。

此时你有一些问题：递归的 $f=A^2\times B$ 不一定满足 $(A,B)$ 互素，$(A,B)$ 可能有重复因子。

我们的思路是：分离奇偶幂和一次幂 $f=\prod A_i^{2p_i}\prod B_i^{2q_i+1}\prod C_i$

然后直接求解 $\prod C_i$ 部分的分解，递归 $\prod A_i^{p_i}$ 和 $\prod B_i^{q_i}$ 去分解，并且记录原来是 $2p_i$ 和 $2q_i+1$。

这样做的目的是每次分出一些不同幂次，正确性显然，最后会分析复杂度。

怎么求 $\prod A,\prod B,\prod C$ 三个部分呢？

先分解出 $A^2B$，然后考虑找到一次式：

取 $g=\gcd(A,B)$，那么 $B/g$ 就是一次式。

然后清空让 $B=1$，不断做：$G=\gcd(g,A),A\gets A/G,B\gets B\times G$。

最终得到的 $A,B\times g$ 就是 $\prod A,\prod B$ 了。

具体实现细节看代码。

复杂度分析

下面分析比较粗略，只能保证大致思路正确。

设最开始的 $\deg$，也就是 bitset 开的长度为 $N$，当前递归到 的多项式 $\deg =n$。

不断 $\gcd$ 出 $A,B,C$ 递归，每次递归区分出指数奇偶性，然后 $/2$。

即每次区分指数的最低二进制位，于是顶多递归 $\log N$ 层。

注意到第一层 $\sum n\sim N$，第二层 $\sum n\sim N/2$，$\cdots$

于是所有层的 $\sum n=\mathcal{O}(N)$。

每次 $\gcd$ 复杂度 $\mathcal{O}(\frac{N^2n}{w})$。

但是分解 $A,B,C$ 那里可能要进行多次 $\gcd$，不过顶多带点 $N^{0.5},\log N$ 啥的，并且有很多 $/2$ 的常熟，所以依然跑很快。

构造矩阵 $D$ 部分有 $x^{2i}\bmod f=x^2(x^{2(i-1)}\bmod f)\bmod f$，直接递推算。复杂度 $\mathcal{O}(\frac{Nn}{w})$。

高斯消元求 $\mathop{\text{rk}}$ 部分，设当前 $\deg$ 为 $n$，bitset 长度为 $N$，则复杂度为 $\mathcal{O}(\frac{Nn^2}{w})$。

于是复杂度最坏为 $\mathcal{O}(\frac{N^{3.5}}{w})$，算上常数啥的和 $\mathcal{O}(\frac{N^{3}}{w})$ 差不多，实际效果也差不多。

跑得非常不满，跑得飞快，吊打标算！

$\bf{code}$

#include<bits/stdc++.h>
#define LL long long
#define vec vector<int>
#define fr(x) freopen(#x".in","r",stdin);freopen(#x".out","w",stdout);
using namespace std;
const int N=2005,mod=998244353;
int id,d,L,ans=1;
inline int ksm(int x,int p){int s=1;for(;p;(p&1)&&(s=1ll*s*x%mod),x=1ll*x*x%mod,p>>=1);return s;}
struct T
{
	bitset<N>a;int n;
	inline void wr(){for(int i=0;i<n;i++) cout<<a[i]<<" ";cout<<"\n";}
	inline auto operator[](int x){return a[x];}
	inline void cl(){while(n&&!a.test(n-1)) n--;}
	inline bool operator==(T x){return a==x.a;}
	inline bool n1(){return !a.test(0)||n!=1;}
	inline void operator^=(T y){a^=y.a;n=max(n,y.n);cl();}
	inline friend T operator*(T x,T y){
		int n=x.n-1,m=y.n-1;T z;
		for(int i=0;i<=m;i++) if(y[i]) z.a^=x.a<<i;
		return z.n=n+m+1,z.cl(),z;
	}
	inline friend T operator%(T x,T y){
		int m=y.n-1;
		for(int i=x.n-1;i>=m;i--) if(x[i]) x.a^=y.a<<(i-m);
		return x.n=y.n,x.cl(),x;
	}
	inline friend T operator/(T x,T y){
		T z;int n=x.n-1,m=y.n-1;z.n=n-m+1;
		for(int i=n;i>=m;i--) if(x[i]) x.a^=y.a<<(i-m),z[i-m]=1;
		return z.cl(),z;
	}
	inline T dv(){
		T x;x.n=n-1;
		for(int i=1;i<n;i+=2) x[i-1]=a[i];
		return x.cl(),x;
	}
	inline T sqrt(){
		T x;x.n=n/2+1;
		for(int i=0;i<n;i+=2) x[i/2]=a[i];
		return x.cl(),x;
	}
}I,a,f[N];
inline T gcd(T x,T y){return !y.n?x:gcd(y,x%y);}
inline void upd(T a,int p)
{
	a.cl();if(a.n<=1) return;L=a.n-1;
	for(int i=0;i<L;i++) f[i].a.reset(),f[i].n=L;
	for(int k=f[0][0]=1;k<L;k++)
	{
		f[k].a=f[k-1].a<<2;
		for(int i:{1,0}) if(f[k][i+L]) f[k].a^=a.a<<i;
	}
	for(int i=0;i<L;i++) f[i][i].flip();
	for(int i=0,t;i<L;i++) for(int j=0;j<i;j++)
		t=f[i][j],f[i][j]=f[j][i],f[j][i]=t;
	int c=0;
	for(int i=0;i<L;i++)
	{
		int w=-1;
		for(int j=c;j<L;j++) if(f[j][i]){w=j;break;}
		if(w<0) continue;if(w^c) swap(f[w],f[c]);
		for(int j=c+1;j<L;j++) if(f[j][i]) f[j]^=f[c];c++;
	}
	ans=1ll*ans*ksm(p+1,L-c)%mod;
}
void dfs(T a,int s,int p)
{
	if(!a.n1()) return;
	T t=a.dv(),b,c;
	if(!t.n) return dfs(a.sqrt(),s,p<<1);
	b=gcd(t,a);a=a/b;swap(a,b);
	c=gcd(a,b);b=b/c;swap(b,c);upd(c,s+p);

	c=I;a=a.sqrt();
	while(1)
	{
		T g=gcd(a,b);
		if(!g.n1()) break;
		c=c*g,a=a/g;
	}
	dfs(a,s,p<<1),dfs(c,s+p,p<<1);
}
int main()
{
	fr(count)
	ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);cin>>id>>d;
	for(int i=0,x;i<=d;i++) cin>>x,a[i]=x;a.n=d+1;
	I.n=I.a[0]=1;
	return dfs(a,0,1),cout<<ans,0;
}

posted @ 2025-06-30 20:36 HaHeHyt 阅读(470) 评论(0) 收藏举报

刷新页面返回顶部

Loading

HaHeHyt's blog

2025 福建省队集训录

鲜花

于 2025/6/30~7/1

2025/7/2

2025/7/4

2025/7/6

目标

\(\scr{Day}\ 1\)

T1 (tree)

T2 (loong)

加入 `X`

加入 `.`

T3 (lush)

\(\scr{Day}\ 2\)

T1 (trans)

T2 (toxic)

T3 (second)

Sub1: q = 0

Sub2: op = 1

Sub3

实现

\(\scr{Day}\ 3\)

T1 (sand)

T2 (tree)

T3 (future)

\(\scr{Day}\ 4\)

T1 (attack)

T2 (light)

T3 (war)

\(\scr{Day}\ 5\)

T1 (plan)

T2 (trans)

T3 (divisors)

\(\scr{Day}\ 6\)

T1 (sort)

T2 (path)

T3 (count)

公告

Loading

HaHeHyt's blog

2025 福建省队集训录

鲜花

于 2025/6/30~7/1

2025/7/2

2025/7/4

2025/7/6

目标

\(\scr{Day}\ 1\)

T1 (tree)

T2 (loong)

加入 X

加入 .

T3 (lush)

\(\scr{Day}\ 2\)

T1 (trans)

T2 (toxic)

T3 (second)

Sub1: q = 0

Sub2: op = 1

Sub3

实现

\(\scr{Day}\ 3\)

T1 (sand)

T2 (tree)

T3 (future)

\(\scr{Day}\ 4\)

T1 (attack)

T2 (light)

T3 (war)

\(\scr{Day}\ 5\)

T1 (plan)

T2 (trans)

T3 (divisors)

\(\scr{Day}\ 6\)

T1 (sort)

T2 (path)

T3 (count)

公告

加入 `X`

加入 `.`