HYLOVEYOURSELF

小洋宝的进步史

导航

Datawhale组队学习😀深入浅出PyTorch Task1

Datawhale组队学习

深入浅出PyTorch-PyTorch基础知识

作者:博客园-岁月月宝贝

基于我自己对Jupyter notebook的了解&PyTorch及相关环境的熟悉,牛学长与他优秀的小伙伴们编写的原教程https://datawhalechina.github.io/thorough-pytorch/(🌟教程编写时间在3年前,所以虽然时效性有限,但是人类编写程度为100%👍) 的第零章与第一章我就不作赘述,大家需要时自取(当然,问国内大模型也很方便😊).还建议大家阅读教程文字版前先听同为Datawhale出品的B站【深入浅出Pytorch】的这个视频: https://www.bilibili.com/video/BV1L44y1472Z/?p=2&share_source=copy_web&vd_source=0c3f112a84e3e961fa46fa4e526e43be ,我最想学的张量等基础知识部分讲得最详细❤

一、张量😊

在深度学习中,各式各样数据的承载方式是"张量",那么张量是什么?请看下图:

image-20250212010436248

我们从左边向右介绍,Scalar是标量,代表数字;Vector是向量,维度为1;Matrix是矩阵,维度为2;Tensor是张量,图上为三维,实际维度不限(所以它这类可以包含前面三种~). 生活中,时间序列常为三维,图像常为4维度,视频可能需要5维,它们都可以用"张量"来表示!

其实,在 PyTorch 中，torch.Tensor 是一种用于存储和变换数据的数据结构类型。如果你之前使用过 NumPy，你会发现在结构和操作方面，Tensor 和 NumPy 的多维数组（如 numpy.ndarray）非常相似。它们都支持多维数据的索引、切片、基本运算等操作(参见官方文档)。但Tensor 比 NumPy 的多维数组更强大之处在于, 通过简单的 .cuda() 方法,Tensor就能让运算在 GPU 上进行，从而大大加快训练和推理的速度。而 NumPy 的多维数组只基于 CPU 运算。另外,PyTorch 的 Tensor 通过 .requires_grad 属性可以记录所有的计算操作，并在需要时自动计算出梯度, 而NumPy 的多维数组通常需要用户手动实现. 这些使得 Tensor 非常适合用于深度学习的开发😀.

传说,张量是PyTorch运算的基本单元,且支持基础数据定义和运算,那么下面我们就来小试牛刀!

⚒下面用到的代码来自[thorough-pytorch/notebook/第二章 PyTorch基础知识/代码演示：PyTorch基础知识.ipynb at main · datawhalechina/thorough-pytorch](https://github.com/datawhalechina/thorough-pytorch/blob/main/notebook/第二章 PyTorch基础知识/代码演示：PyTorch基础知识.ipynb)

import torch
torch.tensor

如果你用的也是Pycharm,把鼠标放到torch.tensor上就可以看到:

image-20250212013220368

dtype:用于强制类型转化;device:限制GPU/CPU;requires_grad:是否允许求导;pin_memory:是否把他放到内存中,如果true就是放入内存和显存,用空间换时间.

import torch
# torch.tensor

# 创建tensor，用dtype指定类型。注意类型要匹配
a = torch.tensor(1.0, dtype=torch.float)
b = torch.tensor(1, dtype=torch.long)
c = torch.tensor(1.0, dtype=torch.int8)
print(a, b, c)

输出如下(强制类型转换):

image-20250212013919533

PS:如果只变类型,还可以这样重置: x = torch.randn_like(x, dtype=torch.float)

下面是创建指定类型的tensor:

# 使用指定类型函数随机初始化指定大小的tensor
d = torch.FloatTensor(2,3)
e = torch.IntTensor(2)
f = torch.IntTensor([1,2,3,4])  #对于python已经定义好的数据结构可以直接转换
print(d, '\n', e, '\n', f)

输出如下(需要指定长宽/浮点数等):

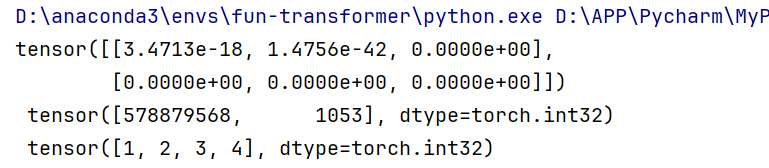
image-20250212014302543

接着,我们试试它与numpy的相互转化!

# tensor和numpy array之间的相互转换
import numpy as np

g = np.array([[1,2,3],[4,5,6]])
h = torch.tensor(g)
print(h)
i = torch.from_numpy(g)
print(i)
j = h.numpy()
print(j)

成功转化:

image-20250212014701789

下面是一条关于"独立变量"的注意事项:

torch.tensor创建得到的张量和原数据是不共享内存的，张量对应的变量是独立变量。
而torch.from_numpy() 和torch.as_tensor() 从numpy array 创建得到的张量和原数据是共享内存的，张量对应的变量不是独立变量，修改numpy array 会导致对应tensor 的改变。

OK 下面我们来看构造Tensor的常见函数🎉

# 常见的构造Tensor的函数
k = torch.rand(2, 3) 
l = torch.ones(2, 3)
m = torch.zeros(2, 3)
n = torch.arange(0, 10, 2)
print(k, '\n', l, '\n', m, '\n', n)

结果如下,大家自己找规律:

image-20250212015835956

PS:还可以基于原来矩阵的torch.dtype和torch.device,创建一个新的全1矩阵,如k = k.new_ones(4, 3, dtype=torch.double) ,不过还可以k = torch.ones(4, 3, dtype=torch.double)

构造好了Tensor,那请问我们怎么查看维度呢?

k = torch.rand(2, 3)
# 查看tensor的维度信息（两种方式）
print(k.shape)
print(k.size())

输出:

image-20250212020150620

可见的确2行3列!

下面,我们来用张量作加法:

k = torch.rand(2, 3)
print(k)
o = torch.ones(2, 3)

# 方式1
print(k + o)

# 方式2
print(torch.add(k,o)) 

# 方式3 in-place，原值修改
o.add_(k) 
print(o)

输出如下:

image-20250212022543321

那么,tensor的索引方式是?

与numpy类似,索引出来的结果与原数据共享内存，修改一个，另一个会跟着修改。

你可以试试:

import torch
x = torch.rand(4,3)
# 取第二列
print(x[:, 1]) 
y = x[0,:]#获取了第一行的数据
y += 1
print(y)
print(x[0, :]) # 源tensor也被改了了

结果发现 x[0, :] 也变成了加 1 之后的结果(*^_^*)

但是如果

import torch

x = torch.rand(4, 3)
print("Original x:", x)

# 取第一行并创建一个副本
y = x[0, :].copy()
y += 1
print("Modified y:", y)
print("Original x after modification:", x[0, :])

你会发现y 被修改了，但 x[0, :] 保持不变. 这说明使用 copy() 方法创建了一个新的 Tensor，不再和原 Tensor 共享内存。

接着,我想了解张量形状改变的容易程度,于是

k = torch.rand(2, 3)
o = torch.ones(2, 3)
o.add_(k) 
print(o)
# 改变tensor形状的神器：view
print(o.view((3,2)))
print(o.view(-1,2))# -1是指这一维的维数由其他维度决定

输出如下:

image-20250212024159780

可以发现,torch.view()会改变原始张量，但是很多情况下，我们希望原始张量和变换后的张量互相不影响。推荐的方法是我们先用 clone() 创造一个张量副本(会被记录在计算图中，即梯度回传到副本时也会传到源 Tensor 👍), 然后再使用 torch.view()进行函数维度变换 。

前面讲到了创造张量，现在就讲取值！是否有办法不打草惊蛇的取到value?

import torch
x = torch.randn(1)
print(x.item())
print(type(x))
print(type(x.item()))

可以使用 .item() 来获得这个 value：

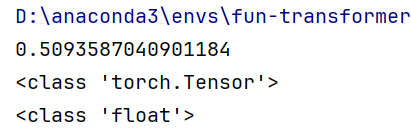
image-20250212030435843

最后，我们来讲张量的两个易错点：

1.广播机制

当对两个形状不同的 Tensor 按元素运算时，可能会触发广播(broadcasting)机制：先适当复制元素使这两个 Tensor 形状相同后再按元素运算。

# tensor的广播机制（使用时要注意这个特性）
p = torch.arange(1, 3).view(1, 2)
print(p)
q = torch.arange(1, 4).view(3, 1)
print(q)
print(p + q)

输出如下：

image-20250212031005273

2.扩展&压缩

PS：下面的o没有经过view操作

# 扩展&压缩tensor的维度：squeeze
print(o)
r = o.unsqueeze(1)#独立变量
print("扩展维度1后的")
print(r)
print(r.shape)

s = r.squeeze(0)
print("压缩维度0后的")
print(s)
print(s.shape)

t = r.squeeze(1)
print("压缩维度1后的")
print(t)
print(t.shape)

下图可以看到只有哪个维度被拓展(维度==1)，哪个维度才能被压缩：

image-20250212032231995

二、自动求导😊

为什么要自动求导呢？因为要沿着梯度下降的方向才能找到目标函数的最优解！

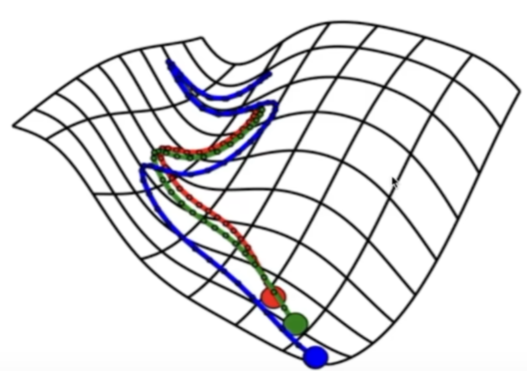
image-20250212033104252

细致到代码实现，autograd 是 PyTorch 中实现自动求导的核心包。它允许用户对张量（torch.Tensor）上的操作进行自动求导，从而计算梯度。这是深度学习中反向传播的基础。Tensor数据结构是实现自动求导的基础。

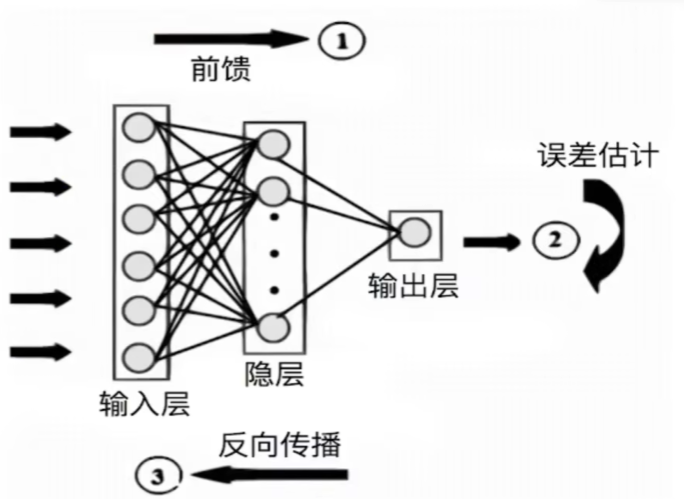
image-20250212033633286

全流程：①输入数据，正向传播；②同时创建计算图；③计算损失函数；④损失函数反向传播；⑤更新模型参数。

autograd 的工作原理

autograd 是一个 运行时定义（define-by-run） 的框架。这意味着：

  • 动态计算图：每次运行代码时，autograd 会根据代码的执行动态构建计算图。
  • 反向传播：计算图用于反向传播，自动计算梯度。
  • 灵活性：每次迭代可以有不同的计算图，非常适合动态模型（如循环神经网络）。

自动求导——数学基础

  • 多元函数求导的雅克比矩阵

    \[J = \begin{pmatrix} \frac{\partial y_1}{\partial x_1} & \cdots & \frac{\partial y_1}{\partial x_n} \\ \vdots & \ddots & \vdots \\ \frac{\partial y_m}{\partial x_1} & \cdots & \frac{\partial y_m}{\partial x_n} \end{pmatrix} \]

  • 复合函数求导的链式法则
    若 $ h(x) = f(g(x)) $，则 $ h'(x) = f'(g(x)) \cdot g'(x) $

  • PyTorch自动求导提供了计算雅克比乘积的工具
    损失函数 $ l $ 对输出 $ y $ 的导数是：

    \[v = \begin{pmatrix} \frac{\partial l}{\partial y_1} & \cdots & \frac{\partial l}{\partial y_m} \end{pmatrix} \]

    那么 $ l $ 对输入 $ x $ 的导数就是：

    \[vJ = \begin{pmatrix} \frac{\partial l}{\partial y_1} & \cdots & \frac{\partial l}{\partial y_m} \end{pmatrix} \begin{pmatrix} \frac{\partial y_1}{\partial x_1} & \cdots & \frac{\partial y_1}{\partial x_n} \\ \vdots & \ddots & \vdots \\ \frac{\partial y_m}{\partial x_1} & \cdots & \frac{\partial y_m}{\partial x_n} \end{pmatrix} = \begin{pmatrix} \frac{\partial l}{\partial x_1} & \cdots & \frac{\partial l}{\partial x_n} \end{pmatrix} \]

自动求导——动态计算图(DCG)

DCG = 张量 + 运算

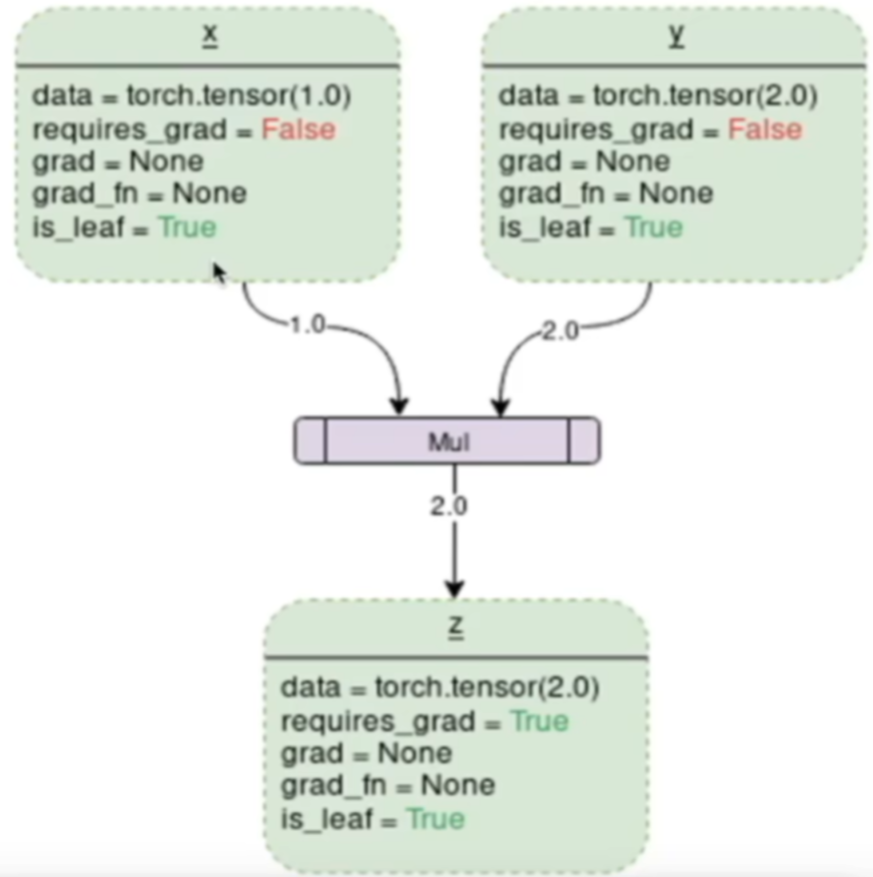
image-20250212035254911

如果设置它的属性 .requires_grad 为 True，那么它将会追踪对于该张量的所有操作。当完成计算后可以通过调用 .backward()，来自动计算所有的梯度。这个张量的所有梯度将会自动累加到.grad属性。

要阻止一个张量被跟踪历史，可以调用.detach()方法将其与计算历史分离，并阻止它未来的计算记录被跟踪。为了防止跟踪历史记录(和使用内存），可以将代码块包装在 with torch.no_grad(): 中。

既然有动态图，就有静态图，它们最大的区别在于静态图不需要预先定义计算图的结构，而动态图需要：

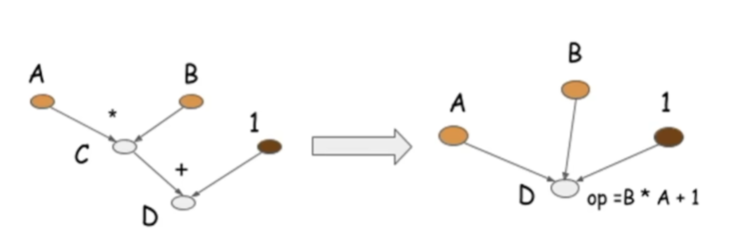
image-20250212035751984

实践部分

下面，我们通过一个简单的函数 $$y=x_1+2∗x_2$$ 来说明PyTorch自动求导的过程

import torch

x1 = torch.tensor(1.0, requires_grad=True)
x2 = torch.tensor(2.0, requires_grad=True)
y = x1 + 2*x2
print(y)

输出为5，说明正向传播成功：

image-20250212040118284

接下来我们查看导数是否要计算&其是否存在

# 首先查看每个变量是否需要求导
print(x1.requires_grad)
print(x2.requires_grad)
print(y.requires_grad)

# 查看每个变量导数大小。此时因为还没有反向传播，因此导数都不存在
print(x1.grad.data)
print(x2.grad.data)
print(y.grad.data)

有趣的事情发生了：

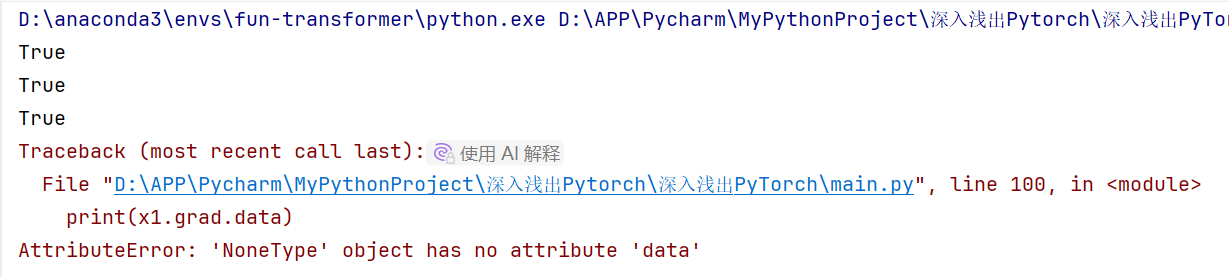
image-20250212040446215

变量都需要求导，但是导数不存在，因为没有反向传播！

PS：x1可测得张量值存在

那么我们试试反向传播：

# 反向传播后看导数大小
y = x1 + 2*x2
y.backward()
print(x1.grad.data)
print(x2.grad.data)

经过反向传播，梯度被记录到“计算图”里了，自然可以取出来😀

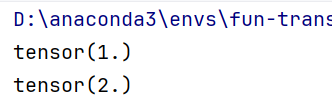
image-20250212040859130

其他特征——导数的累积：

# 导数是会累积的，重复运行相同命令，grad会增加
y = x1 + 2*x2
y.backward()
print(x1.grad.data)
print(x2.grad.data)

输出：

image-20250212041043967

💡所以每次计算前需要清除当前导数值避免累积，这一功能可以通过pytorch的optimizer实现。

大胆尝试:阻断x1,x2求导权利：

# 尝试，如果不允许求导，会出现什么情况？
x1 = torch.tensor(1.0, requires_grad=False)
x2 = torch.tensor(2.0, requires_grad=False)
y = x1 + 2*x2
y.backward()

输出：

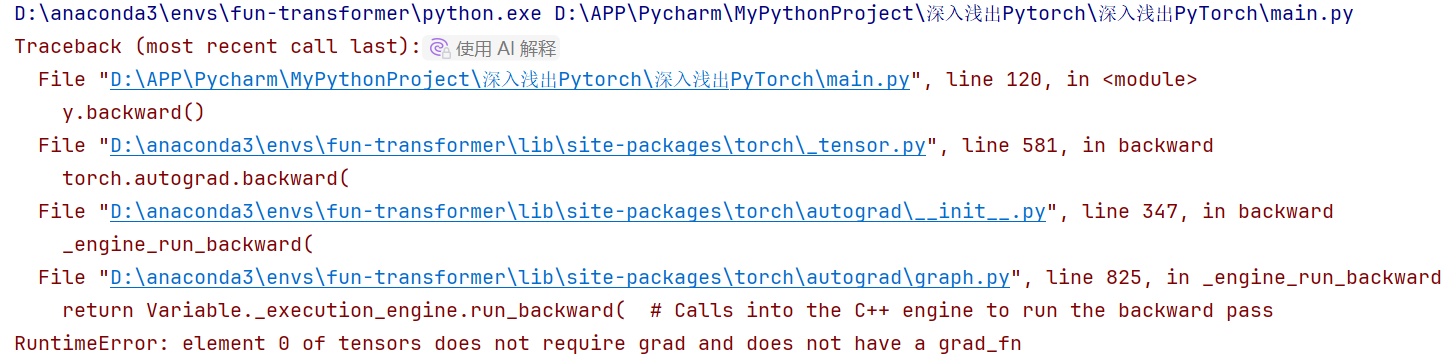
image-20250212041455127

可见反向传播无法完成😘

细节补充

  • requires_grad=True 用于追踪张量的计算历史。
  • .backward() 方法用于计算导数，标量不需要参数，非标量需要指定 gradient 参数。
  • .requires_grad_() 方法可以原地改变张量的 requires_grad 标志。
# 创建一个张量并设置 requires_grad=True 用来追踪其计算历史
x = torch.ones(2, 2, requires_grad=True)  # tensor([[1., 1.], [1., 1.]], requires_grad=True)
print(x)

# 对这个张量做一次运算
y = x ** 2  # tensor([[1., 1.], [1., 1.]], grad_fn=<PowBackward0>)
print(y)

# y 是计算的结果，所以它有 grad_fn 属性
print(y.grad_fn)  # <PowBackward0 object at 0x000001CB45988C70>

# 对 y 进行更多操作
z = y * y * 3  # tensor([[3., 3.], [3., 3.]], grad_fn=<MulBackward0>)
out = z.mean()  # tensor(3., grad_fn=<MeanBackward0>)
print(z, out)

# .requires_grad_(...) 原地改变了现有张量的 requires_grad 标志
a = torch.randn(2, 2)  # 默认 requires_grad = False
a = ((a * 3) / (a - 1))  # 默认情况下 requires_grad 仍为 False
print(a.requires_grad)  # False

# 原地设置 requires_grad 为 True
a.requires_grad_(True)  # 现在 a 的 requires_grad 为 True
print(a.requires_grad)  # True

# 对 a 进行操作并查看 grad_fn
b = (a * a).sum()  # tensor(..., grad_fn=<SumBackward0>)
print(b.grad_fn)  # <SumBackward0 object at 0x000001CB4A19FB50>
  • 雅可比向量积的计算：
    • 在深度学习中，经常需要计算雅可比矩阵的乘积，而不是完整的雅可比矩阵。这是因为完整的雅可比矩阵可能非常大，计算和存储成本很高。
    • backward(v) 方法允许用户传递一个向量 v，计算雅可比矩阵与该向量的乘积，从而避免了计算完整的雅可比矩阵。
  • 阻止 autograd 跟踪计算历史：
    • 在某些情况下，例如模型评估或推理阶段，不需要计算梯度，可以使用 with torch.no_grad(): 代码块来禁用梯度计算。
    • 这样可以节省内存和计算资源，提高代码的运行效率。
  • 修改张量值而不影响计算图：
    • 有时需要直接修改张量的值，但不希望这些修改影响反向传播。可以通过操作 tensor.data 来实现。
    • tensor.data 是一个独立于计算图的张量，修改它不会影响计算图的结构和梯度传播。
# 创建一个张量并设置 requires_grad=True 用来追踪其计算历史
x = torch.randn(3, requires_grad=True)  # tensor([-0.9332,  1.9616,  0.1739], requires_grad=True)
print(x)

# 对这个张量做一次运算
y = x * 2  # tensor([-1.8664,  3.9232,  0.3478], grad_fn=<MulBackward0>)
i = 0
while y.data.norm() < 1000:  # 当 y 的范数小于 1000 时，继续循环
    y = y * 2  # 每次将 y 乘以 2
    i = i + 1  # 计数器加 1
print(y)  # tensor([-477.7843, 1004.3264,   89.0424], grad_fn=<MulBackward0>)
print(i)  # 8

# 在这种情况下，y 不再是标量。torch.autograd 不能直接计算完整的雅可比矩阵，
# 但是如果我们只想要雅可比向量积，只需将这个向量作为参数传给 backward：
v = torch.tensor([0.1, 1.0, 0.0001], dtype=torch.float)  # 定义一个向量 v
y.backward(v)  # 计算雅可比向量积

print(x.grad)  # tensor([5.1200e+01, 5.1200e+02, 5.1200e-02])

# 也可以通过将代码块包装在 with torch.no_grad(): 中，
# 来阻止 autograd 跟踪设置了.requires_grad=True的张量的历史记录。
print(x.requires_grad)  # True
print((x ** 2).requires_grad)  # True

with torch.no_grad():  # 在这个上下文中，autograd 不会跟踪张量的历史记录
    print((x ** 2).requires_grad)  # False

# 如果我们想要修改 tensor 的数值，但是又不希望被 autograd 记录（即不会影响反向传播），
# 那么我们可以对 tensor.data 进行操作。
x = torch.ones(1, requires_grad=True)  # 创建一个张量 x，设置 requires_grad=True

print(x.data)  # tensor([1.])  # 还是一个 tensor
print(x.data.requires_grad)  # False  # 但是已经是独立于计算图之外

y = 2 * x  # y = 2 * x
x.data *= 100  # 只改变了值，不会记录在计算图，所以不会影响梯度传播

y.backward()  # 计算梯度
print(x)  # tensor([100.], requires_grad=True)  # 更改 data 的值也会影响 tensor 的值
print(x.grad)  # tensor([2.])

三、并行计算简介 😊

image-20250212044717512

1 为什么要做并行计算

  • 深度学习依赖算力：GPU 的出现让模型训练更快、更好。🚀
  • PyTorch 并行计算：通过多个 GPU 参与训练，减少训练时间。⏳
  • 查看 GPU 信息：使用 nvidia-smi 命令查看 GPU 使用情况。💻

2 为什么需要 CUDA

  • CUDA 是 NVIDIA 的 GPU 并行计算框架：用于 GPU 编程。💻
  • PyTorch 中的 CUDA：表示将模型或数据迁移到 GPU 上进行计算。🔄
  • 使用 .cuda() 方法：将模型或数据从 CPU 迁移到 GPU（默认 0 号 GPU）。➡️
  • 注意事项：
    • 使用 .cuda() 而不是 .gpu()。❌
    • 只有部分 NVIDIA GPU 支持 CUDA，AMD GPU 使用 OpenCL（PyTorch 不支持）。⚠️
    • 避免频繁在 GPU 和 CPU 之间传递数据，尽量减少数据切换。🔄
    • 简单操作尽量使用 CPU。⚙️

3 常见的并行方法

  1. 网络结构分布到不同的设备中 (Network Partitioning)：

    • 将模型的不同部分拆分到不同 GPU 上。🧩
    • 问题：GPU 之间的通信成本高，逐渐被淘汰。⚠️

  2. 同一层的任务分布到不同数据中 (Layer-wise Partitioning)：

    • 将同一层的模型拆分到不同 GPU 上。🧩
    • 问题：同步任务加重，通信成本高。⚠️

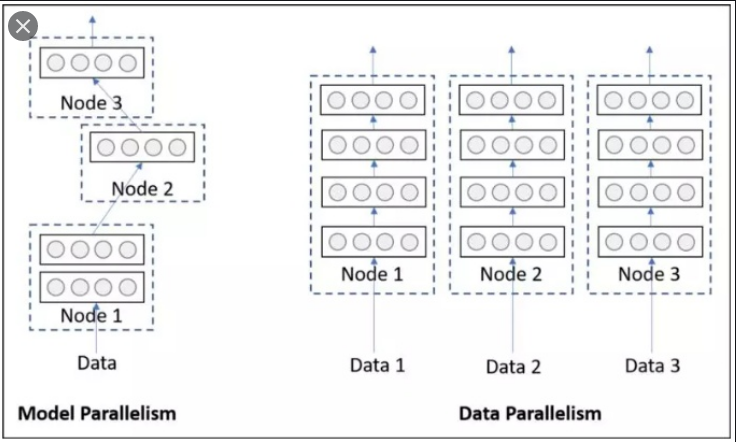
  3. 不同的数据分布到不同的设备中，执行相同的任务 (Data Parallelism)：

    • 将输入数据拆分到不同 GPU 上，每个 GPU 训练一部分数据。🔄
    • 优势：解决通信问题，主流方式。🌟
    数据并行.png

4 使用 CUDA 加速训练

  1. 单卡训练：

    • 将模型和数据迁移到 GPU 上：

      model = Net()
model.cuda()  # 模型迁移到 GPU
for image, label in dataloader:
    image = image.cuda()  # 数据迁移到 GPU
    label = label.cuda()  # 数据迁移到 GPU

  2. 多卡训练：

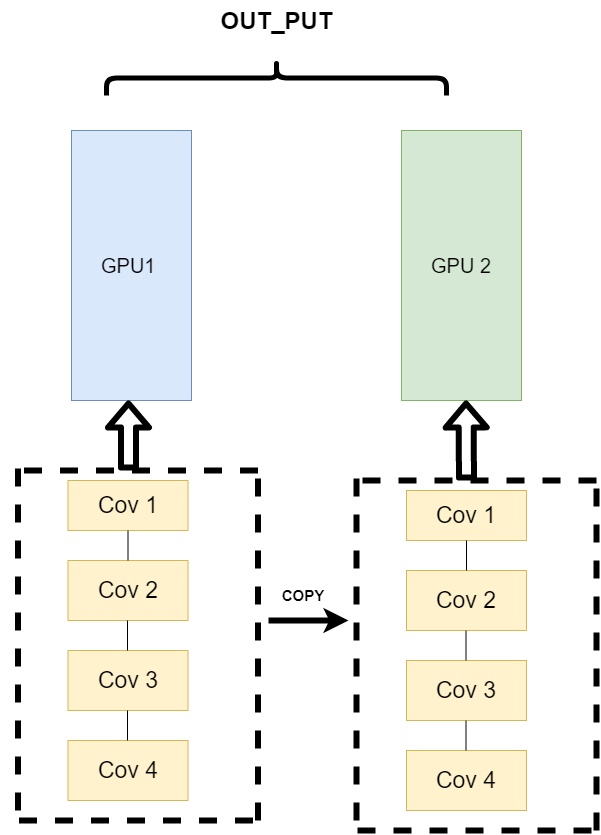
    • DataParallel (DP)：

      DP.png

      • 使用 nn.DataParallel 实现单机多卡训练：

        model = Net()
model.cuda()  # 模型迁移到 GPU
if torch.cuda.device_count() > 1:
    model = nn.DataParallel(model)  # 单机多卡 DP 训练

      • 指定 GPU：

        model = nn.DataParallel(model, device_ids=[0, 1])  # 使用 0 和 1 号 GPU

      • 手动指定 GPU：

        os.environ["CUDA_VISIBLE_DEVICES"] = "1,2"  # 使用 1 和 2 号 GPU

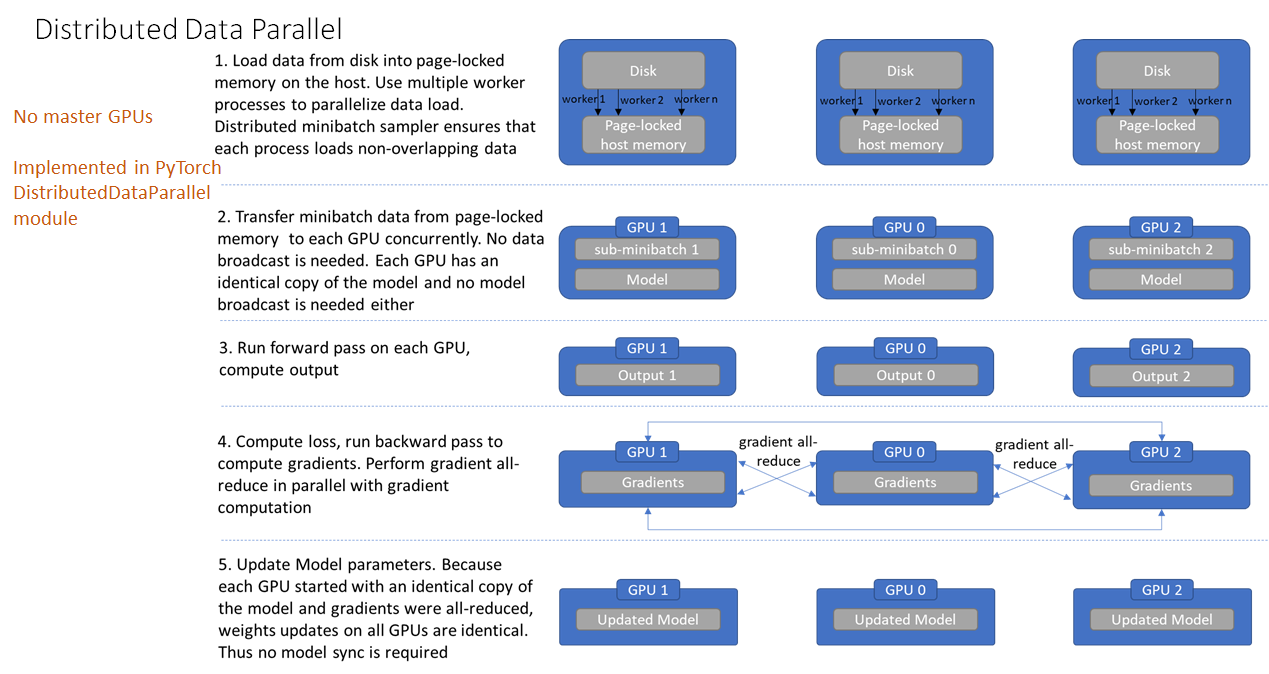
    • DistributedDataParallel (DDP)：

      DP.png

      • 优点：性能更好，负载均衡。🌟

      • 缺点：使用复杂。⚠️

      • 基本用法：

        1. 初始化进程组：

          torch.distributed.init_process_group(backend='nccl')

        2. 创建分布式模型：

          model = torch.nn.parallel.DistributedDataParallel(model, device_ids=[args.local_rank])

        3. 创建分布式数据加载器：

          train_sampler = torch.utils.data.distributed.DistributedSampler(train_dataset)
train_loader = torch.utils.data.DataLoader(train_dataset, batch_size=16, sampler=train_sampler)

        4. 启动 DDP：

          CUDA_VISIBLE_DEVICES=0,1,2,3 python -m torch.distributed.launch --nproc_per_node=4 main.py

  3. DP 与 DDP 的优缺点：

    • DP：
      • 优点：代码简单，一行代码即可实现。👍
      • 缺点：负载不均衡，第一块 GPU 显存占用更多，效率较低。⚠️
    • DDP：
      • 优点：负载均衡，效率高，每个进程独立训练。🌟
      • 缺点：需要修改较多代码，使用复杂。⚠️

总结

  • 并行计算：通过多个 GPU 提升训练速度。🚀
  • CUDA：NVIDIA 的 GPU 并行计算框架，用于将模型和数据迁移到 GPU。🔄
  • 并行方法：数据并行 (Data Parallelism) 是主流方法。🌟
  • CUDA 加速训练：单卡训练简单，多卡训练推荐使用 DDP。👍

四、AI硬件加速设备 😊

1. CPU 和 GPU 🖥️

设备 定义 特点
CPU 中央处理器，电脑的核心配件 处理指令、执行操作、控制时间、处理数据
GPU 图形处理单元 专为图形处理设计，计算速度快，浮点运算能力强

2. 专用集成电路 (ASIC) 🖥️

  • 定义：为实现特定要求而定制的芯片。
  • 优点：高性能、低功耗、高可靠性、高集成度。
  • 缺点：开发周期长，功能难以扩展。

3. TPU (Tensor Processing Unit) 🖥️

  • 定义：谷歌为优化 TensorFlow 框架而设计的专用芯片。
  • 芯片架构设计：
    • Matrix Multiply Unit (MMU)：包含 256x256 个 MAC 部件，每个部件执行 8 位乘加操作。
    • 脉动阵列 (Systolic Array)：数据一波一波地流过芯片，类似于心脏跳动供血的方式。
  • 技术特点：
    • AI 加速专用：特定领域架构，单线程控制，定制指令集。
    • 脉动阵列设计：在一个时钟周期内处理数十万次矩阵运算。
    • 确定性功能和大规模片上内存：片上内存占芯片面积的 35%，减少片外数据访存能耗。

4.NPU (Neural-network Processing Unit) 🖥️

  • 定义：采用“数据驱动并行计算”的架构，特别擅长处理视频、图像类的海量多媒体数据。
  • DianNao 系列架构：
    • DianNao：小尺寸、高吞吐量的加速器。
    • DaDianNao：多核升级版本，支持训练任务。
    • ShiDianNao：机器视觉专用加速器，使用二维运算阵列。
    • PuDianNao：异构运算单元，支持多种机器学习算法。

5. 总结 🌟

  • CPU 和 GPU：通用处理器，适用于多种任务。
  • ASIC：专用定制芯片，高性能、低功耗，但开发周期长。
  • TPU：谷歌设计的专用芯片，优化 TensorFlow 框架，适用于深度学习加速。
  • NPU：寒武纪设计的专用芯片，适用于神经网络深度学习，支持多种算法。

就到这里~谢谢大家！！！

posted on 2025-02-12 02:52  岁月月宝贝  阅读(125)  评论(0)    收藏  举报