CG2017 PA1-2 Crossroad (十字路口) 暴力求解
Description (描述)
City Beiotic is expanding rapidly due to its even more rapidly increasing population. A new district named Kaidian is now under design and you are asked to help with the geometric issues. Specifically, given the thematic map of roads, you need to locate all the crossroads where traffic lights should be installed. A road here might be represented as a segment, a ray, a line or a circle. As your first task, can you tell us how many traffic lights we need to install?
城市Beiotic正在快速扩张,以应对更为快速增长的人口。其中Kaidian区正在规划,需要你来协助解决一些几何问题。你将会得到一张描述街道情况的主题地图,你需要据此确定哪些道路之间是相交的,以便安装红绿灯。不过这里道路形状各异,有的是线段,有的是射线,有的是直线,还有的是圆。情况感觉有些复杂,但你能首先告诉我们一共需要安装多少处红绿灯么?
Input (输入)
The first line consists of four integers delimited by spaces, which are the numbers of different types of roads respectively: S for segments, R for rays, L for lines, and C for circles.
Each of the following S lines describes a segment road. A segment road connecting (x, y) and (u, v) is represented as four integers x, y, u and v, delimited by a space.
Each of the following R lines describes a ray road. A ray road starting from (x, y) and running through (u, v) is represented as four integers x, y, u and v, delimited by a space.
Each of the following L lines describes a line road. A line road running through (x, y) and (u, v) is represented as four integers x, y, u and v, delimited by a space.
Each of the last C lines describes a circle road. A circle road centered at (x, y) and with a radius r is represented as three integers x, y and r, delimited by a space.
第一行是以空格分隔的四个整数,依次是线段(S)、射线(R)、直线(L)和圆(C)类型道路的数目。
接下来的S行各含四个由空格分隔的整数x、y、u、v,对应的线段型道路联接于(x, y)和(u,v)之间。
再接下来的R行也各含四个由空格分隔的整数x、y、u、v,对应的射线型道路起始于(x, y),并穿过(u,v)。
再接下来的L行仍各含四个由空格分隔的整数x、y、u、v,对应的直线型道路穿过(x, y)和(u, v)。
最后的C行各含三个由空格分隔的整数x、y、r,对应的圆型道路以(x, y)为中心,以r为半径。
Output (输出)
Output the total number k of all crossroads between the roads.
输出所有道路之间交点的总数k即可。
Input Samples (样例输入)
3 3 3 3
6 18 49 39
80 29 67 34
90 76 10 4
91 39 69 -1
53 57 8 -36
37 19 85 -67
56 30 106 25
24 23 65 -33
40 9 66 55
22 58 12
13 11 7
1 23 1
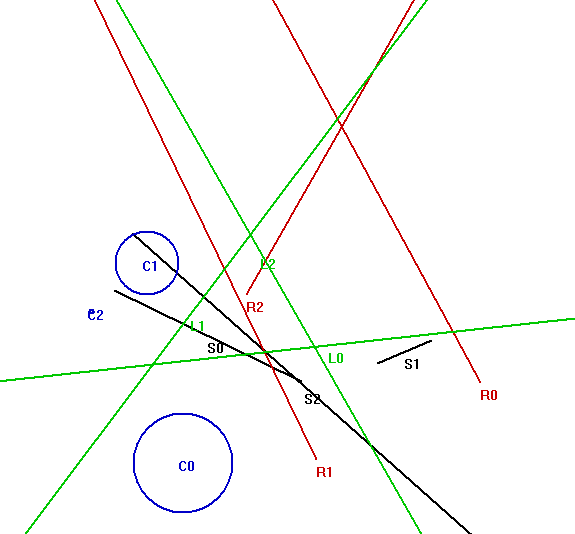
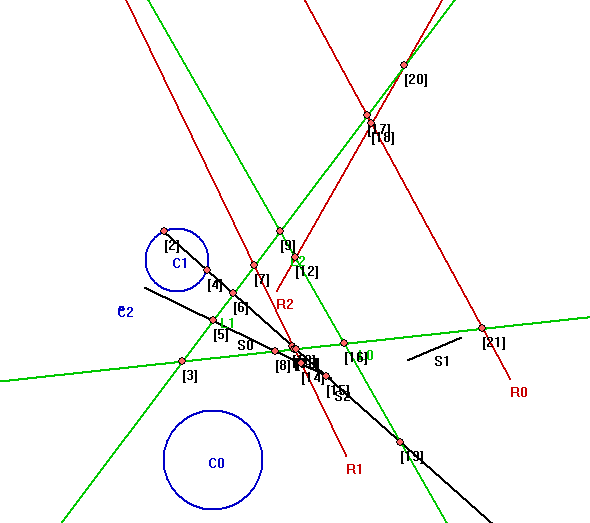
In the image above, segment roads are colored as black; rays, red; lines, green; and circles, blue.
上图中,黑色、红色、绿色、蓝色分别对应于线段型、射线型、直线型、圆型道路。
Output Samples (样例输出)
22
Limitation (限制)
- 2 ≤ S + R + L + C ≤ 20000
- All the coordinates and the radius are integers in (-10^5, 10^5).
- Any pair of roads can intersect at a finite number of points.
- The following cases are all regarded as one generalized crossroad:
- Two roads share a common endpoint, i.e., a turn.
- A road runs through one or two endpoints of another, i.e., a T-shaped crossing or a chord.
- More than two roads intersect at a common point, i.e., a multi-way crossroad
- Time Limit: 2 sec
- Space Limit: 512 MB
- 2 ≤ S + R + L + C ≤ 20000
- 所有坐标和半径均为整数,取值范围为(-10^5, 10^5)
- 任何一对道路至多交于有限个点
- 以下情况作为十字路口的特例,均需予以报告:
- 两条道路首尾衔接(拐弯)
- 一条道路穿过另一条的端点(丁字路口),以及
- 多条道路同时穿过一个点(多岔路口)
- 时间限制:2 sec
- 空间限制:512 MB




Hint (限制)
Segment, line and ray roads can be processed similarly. Circle roads can be broken into a number of arcs.
线段、直线和射线道路的处理方法类似。圆形道路可以分解为若干段圆弧
代码
十分暴力的代码,主要用来练练手。
最终得分 72.5,最后几个案例time exceed。
截图留念吧,时间有限就不优化了。
正解请参考https://architecture.pub/articles/280083500.html
#include<iostream>
#include<vector>
#include<algorithm>
#include<queue>
#include<set>
#include<cmath>
using namespace std;
#define EPS 1e-8
//#define DEBUG
int TOTAL;
enum CURVETYPE{
CNONE, SEGMENT, RAY, LINE, CIRCLE
};
enum POINTTYPE{
PNONE, LEFT, RIGHT, ENDPOINT, DIR, CENTER, INTX
};
struct Point2{
double x;
double y;
// 点所在的曲线编号
long long int n;
POINTTYPE ptype;
// 交点所在的曲线编号
long long int n1;
long long int n2;
Point2(double xx, double yy, long long int nn, POINTTYPE e) : x(xx), y(yy), n(nn), ptype(e){
n1 = 0;
n2 = 0;
}
Point2() : x(0),y(0),n(0),ptype(POINTTYPE::PNONE),n1(0),n2(0){}
bool operator== (const Point2& p) const{
return abs(x - p.x) < EPS && abs(y - p.y) < EPS && ptype == p.ptype && n == p.n && n1 == p.n1 && n2 == p.n2;
}
//需要最大堆,对小于号重载
bool operator < (const Point2& p) const{
return (x < p.x) || (abs(x - p.x) < EPS &&
(y < p.y || (abs(y - p.y) < EPS &&
(ptype < p.ptype || (ptype == p.ptype &&
(n < p.n || (n == p.n &&
n1 < p.n1 || (n1 == p.n1 &&
n2 < p.n2))))))));
}
Point2 operator- (const Point2& p) const{
auto res = Point2();
res.x = x - p.x;
res.y = y - p.y;
return res;
}
Point2 operator+ (const Point2& p) const{
auto res = Point2();
res.x = x + p.x;
res.y = y + p.y;
return res;
}
double operator* (const Point2& p) const{
return x * p.x + y * p.y;
}
Point2 operator* (const double k) const{
auto res = *this;
res.x *= k;
res.y *= k;
return res;
}
double norm(){
return sqrt(x * x + y * y);
}
// 需要最小堆,对大于号重载
friend bool operator > (const Point2& p1, const Point2& p2) {
return (p1.x > p2.x) || (abs(p1.x - p2.x) < EPS &&
(p1.y > p2.y || (abs(p1.y - p2.y) < EPS &&
(p1.ptype > p2.ptype || (p1.ptype == p2.ptype &&
(p1.n > p2.n || (p1.n == p2.n &&
(p1.n1 > p2.n1 || (p1.n1 == p2.n1 &&
p1.n2 >p2.n2)))))))));
}
friend ostream& operator<<(ostream& out, const Point2& p){
string str[] = {"PNONE", "LEFT", "RIGHT", "ENDPOINT", "DIR", "CENTER", "INTX"};
if(p.ptype != INTX)
out << "( " << p.x << " , " << p.y << " ) " << p.n << " " << str[p.ptype] << endl;
else
out << "( " << p.x << " , " << p.y << " ) " << p.n1 << " " << p.n2 << " " << str[p.ptype] << endl;
return out;
}
};
vector<Point2> vecPoints;
class Curve{
public:
// 曲线编号
int n;
CURVETYPE ctype;
Curve(){
n = 0;
ctype = CURVETYPE::CNONE;
}
Curve(int nn, CURVETYPE ct) : n(nn), ctype(ct){}
//虚函数得实现,不然没有vtable
virtual void intersection(Curve*& c, set<Point2>& intxPoints){
cout << "Curve intersection" << endl;
};
bool getLineIntxLinePoint(Point2& p1, Point2& dir1, Point2& p2, Point2& dir2, double& t0, double& t1){
if(abs(abs(dir1 * dir2) - 1) < EPS)
return false;
// 解射线方程,然后判断是否在线段内
auto denom = -dir1.x * dir2.y + dir2.x * dir1.y;
auto p = p2 - p1;
t0 = (-p.x * dir2.y + p.y * dir2.x) / denom;
t1 = (p.y * dir1.x - p.x * dir1.y) / denom;
return true;
};
bool getLineIntxCirclePoint(Point2& p, Point2& dir, Point2& center, double r, double& t0, double& t1){
auto p2c = center - p;
auto p2cDdir = p2c * dir;
auto d = (p2c - dir * p2cDdir).norm();
if(d > r)
return false;
t0 = (p2cDdir + sqrt(p2cDdir * p2cDdir - (p2c * p2c - r * r)));
t1 = (p2cDdir - sqrt(p2cDdir * p2cDdir - (p2c * p2c - r * r)));
return true;
}
Point2 getLineIntxPoint(Point2& p, Point2& dir, double t, int n1, int n2){
auto res = Point2();
res.x = p.x + t * dir.x;
res.y = p.y + t * dir.y;
res.ptype = INTX;
res.n1 = n1;
res.n2 = n2;
vecPoints.push_back(res);
return move(res);
}
friend ostream& operator<<(ostream& out, Curve& c);
};
class Segment : public Curve{
public:
Point2 p1;
Point2 p2;
Point2 dir;
// p1 p2的长度
double t;
Segment() : Curve(0, CURVETYPE::SEGMENT){
p1 = Point2();
p2 = Point2();
dir = Point2();
t = 0;
}
Segment(Point2 pp1, Point2 pp2, int nn) : p1(pp1), p2(pp2), Curve(nn, CURVETYPE::SEGMENT){
t = sqrt((pp2.x - pp1.x) * (pp2.x - pp1.x) + (pp2.y - pp1.y) * (pp2.y - pp1.y));
dir = Point2();
dir.ptype = DIR;
dir.n = nn;
dir.x = (pp2.x - pp1.x) / t;
dir.y = (pp2.y - pp1.y) / t;
}
void segIntxSeg(Curve* c, set<Point2>& intxPoints){
auto sc = dynamic_cast<Segment*> (c);
double t0, t1;
if(!getLineIntxLinePoint(p1, dir, sc->p1, sc->dir, t0, t1))
return;
// 解射线方程,然后判断是否在线段内
if(((t0 > 0 || abs(t0 - 0) < EPS) && (t0 < t || abs(t0 - t) < EPS))
&& (t1 > 0 || abs(t1 - 0) < EPS) && (t1 < sc->t || abs(t1 - sc->t) < EPS)) {
intxPoints.insert(getLineIntxPoint(p1, dir, t0, n, sc->n));
TOTAL++;
}
}
void segIntxRay(Curve* c, set<Point2>& intxPoints);
void segIntxLine(Curve* c, set<Point2>& intxPoints);
void segIntxCir(Curve* c, set<Point2>& intxPoints);
void intersection(Curve* c, set<Point2>& intxPoints){
switch (c->ctype)
{
//变量的定义不能放在goto之后
case SEGMENT :
segIntxSeg(c, intxPoints);
break;
case RAY :
segIntxRay(c, intxPoints);
break;
case LINE :
segIntxLine(c, intxPoints);
break;
case CIRCLE :
segIntxCir(c, intxPoints);
break;
default:
break;
}
}
};
class Ray : public Curve{
public:
Point2 p1;
Point2 p2;
Point2 dir;
Ray() : Curve(0, CURVETYPE::RAY){
p1 = Point2();
p2 = Point2();
dir = Point2();
}
Ray(Point2 pp1, Point2 pp2, int nn) : p1(pp1), p2(pp2), Curve(nn, CURVETYPE::RAY){
dir = Point2();
dir.ptype = DIR;
dir.n = nn;
auto len = sqrt((pp2.x - pp1.x) * (pp2.x - pp1.x) + (pp2.y - pp1.y) * (pp2.y - pp1.y));
dir.x = (pp2.x - pp1.x) / len;
dir.y = (pp2.y - pp1.y) / len;
}
void rayIntxRay(Curve* c, set<Point2>& intxPoints){
auto sc = dynamic_cast<Ray*> (c);
double t0, t1;
if(!getLineIntxLinePoint(p1, dir, sc->p1, sc->dir, t0, t1))
return;
// 解射线方程,然后判断是否在线段内
if((t0 > 0 || abs(t0 - 0) < EPS) && (t1 > 0 || abs(t1 - 0) < EPS)) {
intxPoints.insert(getLineIntxPoint(p1, dir, t0, n, sc->n));
TOTAL++;
}
}
void rayIntxLine(Curve* c, set<Point2>& intxPoints);
void rayIntxCir(Curve* c, set<Point2>& intxPoints);
void intersection(Curve* c, set<Point2>& intxPoints){
switch (c->ctype)
{
case SEGMENT :
dynamic_cast<Segment*> (c)->intersection(dynamic_cast<Curve*>(this), intxPoints);
break;
case RAY :
rayIntxRay(c, intxPoints);
break;
case LINE :
rayIntxLine(c, intxPoints);
break;
case CIRCLE :
rayIntxCir(c, intxPoints);
break;
default:
break;
}
}
};
class Line : public Curve{
public:
Point2 p1;
Point2 p2;
Point2 dir;
Line() : Curve(0, CURVETYPE::LINE){
p1 = Point2();
p2 = Point2();
}
Line(Point2 pp1, Point2 pp2, int nn) : Curve(nn, CURVETYPE::LINE){
p1 = pp1;
p2 = pp2;
auto len = sqrt((pp2.x - pp1.x) * (pp2.x - pp1.x) + (pp2.y - pp1.y) * (pp2.y - pp1.y));
dir = Point2();
dir.ptype = DIR;
dir.n = nn;
dir.x = (pp2.x - pp1.x) / len;
dir.y = (pp2.y - pp1.y) / len;
}
void lineIntxLine(Curve* c, set<Point2>& intxPoints){
auto sc = dynamic_cast<Line*> (c);
double t0, t1;
if(!getLineIntxLinePoint(p1, dir, sc->p1, sc->dir, t0, t1))
return;
// 解射线方程,然后判断是否在线段内
intxPoints.insert(getLineIntxPoint(p1, dir, t0, n, sc->n));
TOTAL++;
}
void lineIntxCir(Curve* c, set<Point2>& intxPoints);
void intersection(Curve* c, set<Point2>& intxPoints){
switch (c->ctype)
{
case SEGMENT :
dynamic_cast<Segment*> (c)->intersection(dynamic_cast<Curve*>(this), intxPoints);
break;
case RAY :
dynamic_cast<Ray*> (c)->intersection(dynamic_cast<Curve*>(this), intxPoints);
break;
case LINE :
lineIntxLine(c, intxPoints);
break;
case CIRCLE :
lineIntxCir(c, intxPoints);
break;
default:
break;
}
}
};
class Circle : public Curve{
public:
Point2 center;
double R;
Circle() : Curve(0, CURVETYPE::CIRCLE){
center = Point2();
R = 0;
}
Circle(Point2 cc, double r, int nn) : Curve(nn, CURVETYPE::CIRCLE){
center = cc;
R = r;
}
void cirIntxCir(Curve* c, set<Point2>& intxPoints){
auto cc = dynamic_cast<Circle*>(c);
auto d = (center - cc->center).norm();
if(d > R + cc->R || d < abs(R - cc->R))
return;
// 用变换坐标法
// https://www.cnblogs.com/wangzming/p/8338142.html
auto P1 = Point2();
P1.x = cc->center.x + center.x;
P1.y = cc->center.y + center.y;
auto P2 = Point2();
P2.x = cc->center.x - center.x;
P2.y = cc->center.y - center.y;
auto P3 = Point2();
P3.y = cc->center.x - center.x;
P3.x = cc->center.y - center.y;
auto d2 = d * d;
auto R1_2 = R * R;
auto R2_2 = cc->R * cc->R;
auto A = (R1_2 - R2_2) / (2 * d2);
auto B = sqrt(2 * (R1_2 + R2_2) / (d2) - (R1_2 - R2_2)*(R1_2 - R2_2)/(d2 * d2) - 1) / 2;
auto res = P1 * 0.5 + P2 * A + P3 * B;
res.n1 = n;
res.n2 = cc->n;
res.ptype = INTX;
intxPoints.insert(res);
vecPoints.push_back(res);
TOTAL++;
if(!(abs(d - R - cc->R) < EPS) && !(abs(d - abs(R - cc->R)) < EPS)){
auto res = P1 * 0.5 + P2 * A - P3 * B;
res.n1 = n;
res.n2 = cc->n;
res.ptype = INTX;
intxPoints.insert(res);
vecPoints.push_back(res);
TOTAL++;
}
}
void intersection(Curve* c, set<Point2>& intxPoints){
switch (c->ctype)
{
case SEGMENT :
dynamic_cast<Segment*> (c)->intersection(dynamic_cast<Curve*>(this), intxPoints);
break;
case RAY :
dynamic_cast<Ray*> (c)->intersection(dynamic_cast<Curve*>(this), intxPoints);
break;
case LINE :
dynamic_cast<Line*> (c)->intersection(dynamic_cast<Curve*>(this), intxPoints);
break;
case CIRCLE :
cirIntxCir(c, intxPoints);
break;
default:
break;
}
}
};
// 如果要在Curve类内定义,只能是Segment*,因为前向声明不能使用对象,只能使用指针
ostream& operator<<(ostream& out, Curve& c) {
string str[] = {"CNONE", "SEGMENT", "RAY", "LINE", "CIRCLE"};
if(c.ctype == CNONE)
out << c.n << " " << str[c.ctype] << endl;
else if(c.ctype == SEGMENT) {
// dynamic_cast必须有虚函数
Segment& s = dynamic_cast<Segment&>(c);
out << s.n << " " << str[s.ctype] << " (" << s.p1.x << " , " << s.p1.y << ") (" << s.p2.x << " , " << s.p2.y << ") "
<< s.t << " (" << s.dir.x << " , " << s.dir.y << ")" << endl;
}else if(c.ctype == RAY){
Ray& r = dynamic_cast<Ray&>(c);
out << r.n << " " << str[r.ctype] << " (" << r.p1.x << " , " << r.p1.y << ") " << " (" << r.dir.x << " , " << r.dir.y << ")" << endl;
}else if(c.ctype == LINE){
Line& l = dynamic_cast<Line&>(c);
out << l.n << " " << str[l.ctype] << " (" << l.p1.x << " , " << l.p1.y << ") (" << l.dir.x << " , " << l.dir.y << ") " << endl;
}else if(c.ctype == CIRCLE){
Circle& cc = dynamic_cast<Circle&>(c);
out << cc.n << " " << str[cc.ctype] << " (" << cc.center.x << " , " << cc.center.y << ") " << cc.R << endl;
}
return out;
}
void Segment::segIntxRay(Curve* c, set<Point2>& intxPoints) {
auto sc = dynamic_cast<Ray*> (c);
double t0, t1;
if(!getLineIntxLinePoint(p1, dir, sc->p1, sc->dir, t0, t1))
return;
// 解射线方程,然后判断是否在线段内
if(((t0 > 0 || abs(t0 - 0) < EPS) && (t0 < t || abs(t0 - t) < EPS))
&& (t1 > 0 || abs(t1 - 0) < EPS)) {
intxPoints.insert(getLineIntxPoint(p1, dir, t0, n, sc->n));
TOTAL++;
}
}
void Segment::segIntxLine(Curve* c, set<Point2>& intxPoints){
auto sc = dynamic_cast<Line*> (c);
double t0, t1;
if(!getLineIntxLinePoint(p1, dir, sc->p1, sc->dir, t0, t1))
return;
// 解射线方程,然后判断是否在线段内
if(((t0 > 0 || abs(t0 - 0) < EPS) && (t0 < t || abs(t0 - t) < EPS))) {
intxPoints.insert(getLineIntxPoint(p1, dir, t0, n, sc->n));
TOTAL++;
}
}
void Segment::segIntxCir(Curve* c, set<Point2>& intxPoints){
auto cir = dynamic_cast<Circle*> (c);
double t0, t1;
if(!getLineIntxCirclePoint(p1, dir, cir->center, cir->R, t0, t1))
return;
if(((t0 > 0 || abs(t0 - 0) < EPS) && (t0 < t || abs(t0 - t) < EPS))) {
intxPoints.insert(getLineIntxPoint(p1, dir, t0, n, cir->n));
TOTAL++;
}
if(abs(t0 - t1) > EPS)
if(((t1 > 0 || abs(t1 - 0) < EPS) && (t1 < t || abs(t1 - t) < EPS))) {
intxPoints.insert(getLineIntxPoint(p1, dir, t1, n, cir->n));
TOTAL++;
}
}
void Ray::rayIntxLine(Curve* c, set<Point2>& intxPoints){
auto sc = dynamic_cast<Line*> (c);
double t0, t1;
if(!getLineIntxLinePoint(p1, dir, sc->p1, sc->dir, t0, t1))
return;
// 解射线方程,然后判断是否在线段内
if(((t0 > 0 || abs(t0 - 0) < EPS))) {
intxPoints.insert(getLineIntxPoint(p1, dir, t0, n, sc->n));
TOTAL++;
}
}
void Ray::rayIntxCir(Curve* c, set<Point2>& intxPoints){
auto cir = dynamic_cast<Circle*> (c);
double t0, t1;
if(!getLineIntxCirclePoint(p1, dir, cir->center, cir->R, t0, t1))
return;
if(((t0 > 0 || abs(t0 - 0) < EPS))) {
intxPoints.insert(getLineIntxPoint(p1, dir, t0, n, cir->n));
TOTAL++;
}
if(abs(t0 - t1) > EPS)
if(((t1 > 0 || abs(t1 - 0) < EPS))) {
intxPoints.insert(getLineIntxPoint(p1, dir, t1, n, cir->n));
TOTAL++;
}
}
void Line::lineIntxCir(Curve* c, set<Point2>& intxPoints){
auto cir = dynamic_cast<Circle*> (c);
double t0, t1;
if(!getLineIntxCirclePoint(p1, dir, cir->center, cir->R, t0, t1))
return;
intxPoints.insert(getLineIntxPoint(p1, dir, t0, n, cir->n));
TOTAL++;
if(abs(t0 - t1) > EPS){
intxPoints.insert(getLineIntxPoint(p1, dir, t1, n, cir->n));
TOTAL++;
}
}
int N, S, R, L, C;
// 多态只能用指针,不能用对象,不然会隐式转换对象的内容而产生丢失
vector<Curve*> curves;
set<Point2> intxPoints;
int main(){
curves.push_back(new Curve());
cin >> S >> R >> L >> C;
int a,b,c,d;
for(int i = 1; i <= S + R + L; i ++){
cin >> a >> b >> c >> d;
if(i <= S){
if(a < c)
curves.push_back(new Segment(Point2(a, b, i, LEFT), Point2(c, d, i, RIGHT), i));
else
curves.push_back(new Segment(Point2(c, d, i, LEFT), Point2(a, b, i, RIGHT), i));
}else if(i <= S + R){
curves.push_back(new Ray(Point2(a, b, i, ENDPOINT), Point2(c, d, i, ENDPOINT), i));
}else if(i <= S + R + L){
if(a < c)
curves.push_back(new Line(Point2(a, b, i, ENDPOINT), Point2(c, d, i, ENDPOINT), i));
else
curves.push_back(new Line(Point2(c, d, i, ENDPOINT), Point2(a, b, i, ENDPOINT), i));
}
}
for(int i = S + R + L + 1; i <= S + R + L + C; i ++){
cin >> a >> b >> c;
curves.push_back(new Circle(Point2(a, b, i, CENTER), c, i));
}
#ifndef DEBUG
for(auto c :curves)
cout << *c;
#endif
for(int i = 1; i <= S + R + L + C; i ++) {
if(i <= S){
auto s = dynamic_cast<Segment*> (curves[i]);
for(int j = i + 1; j <= S + L + R + C; j ++){
s->intersection(curves[j], intxPoints);
}
}else if(i <= S + R) {
auto s = dynamic_cast<Ray*> (curves[i]);
for(int j = i + 1; j <= S + L + R + C; j ++){
s->intersection(curves[j], intxPoints);
}
}else if(i <= S + R + L) {
auto s = dynamic_cast<Line*> (curves[i]);
for(int j = i + 1; j <= S + L + R + C; j ++){
s->intersection(curves[j], intxPoints);
}
}else if(i <= S + R + L + C) {
auto s = dynamic_cast<Circle*> (curves[i]);
for(int j = i + 1; j <= S + L + R + C; j ++){
s->intersection(curves[j], intxPoints);
}
}
}
#ifndef DEBUG
for(auto c :intxPoints)
cout << c;
cout << intxPoints.size() << endl;
sort(vecPoints.begin(), vecPoints.end());
for(auto v : vecPoints)
cout << v;
cout << vecPoints.size() << endl;
#endif
cout << TOTAL;
return 0;
}
测试输入
3 3 3 3 -3 -1 0 -3 4 0 -6 0 1 -2 -6 -4 -7 1 -7 -7 -7 -3 4 0 -8 -6 0 -6 2 2 -4 -7 -6 0 -6 -4 2 -1 0 2 -3 -3 3 2 -3 2 4 -2 2
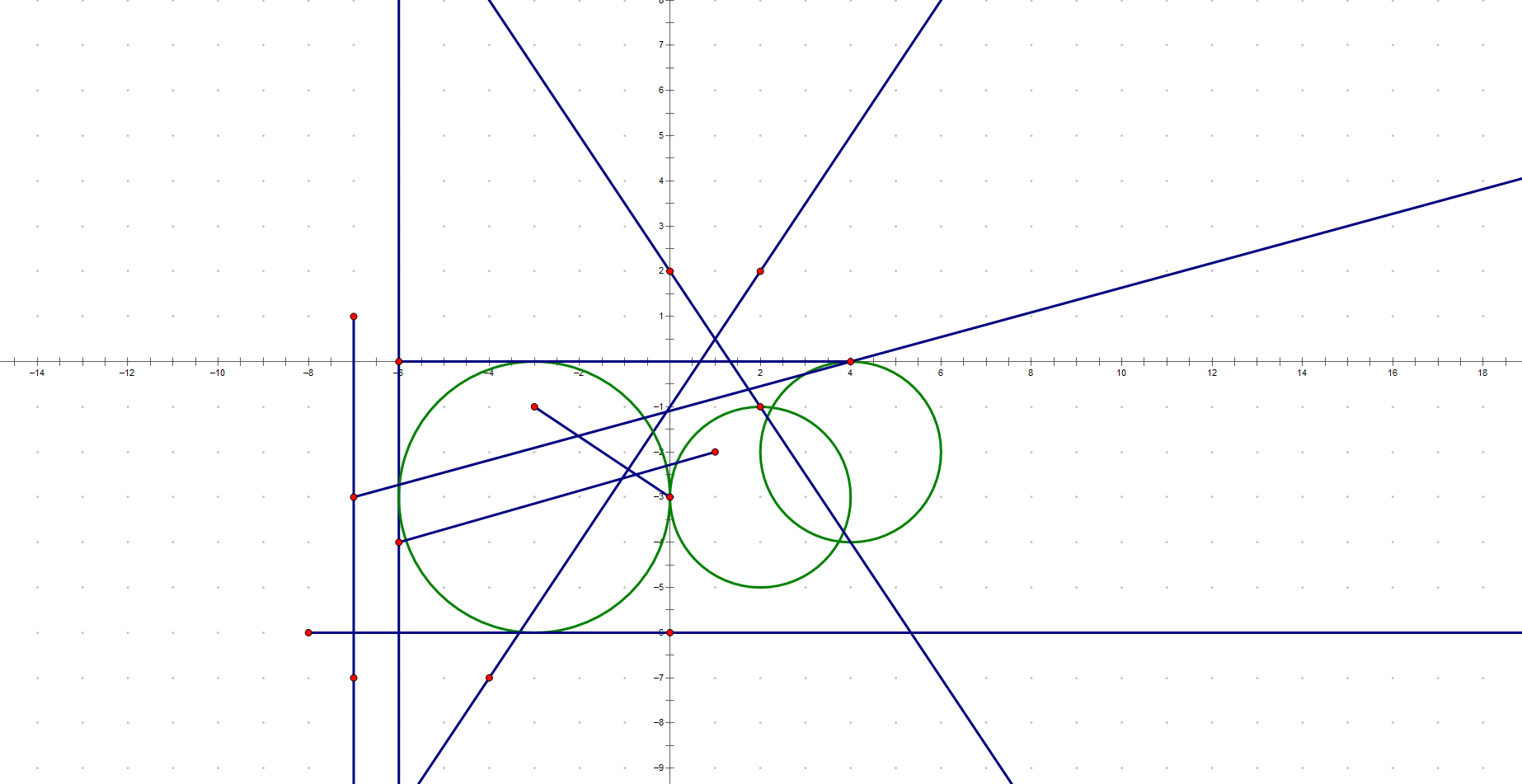
(注:竖直的直线与其他两条直线有画面外的交点)
测试输出
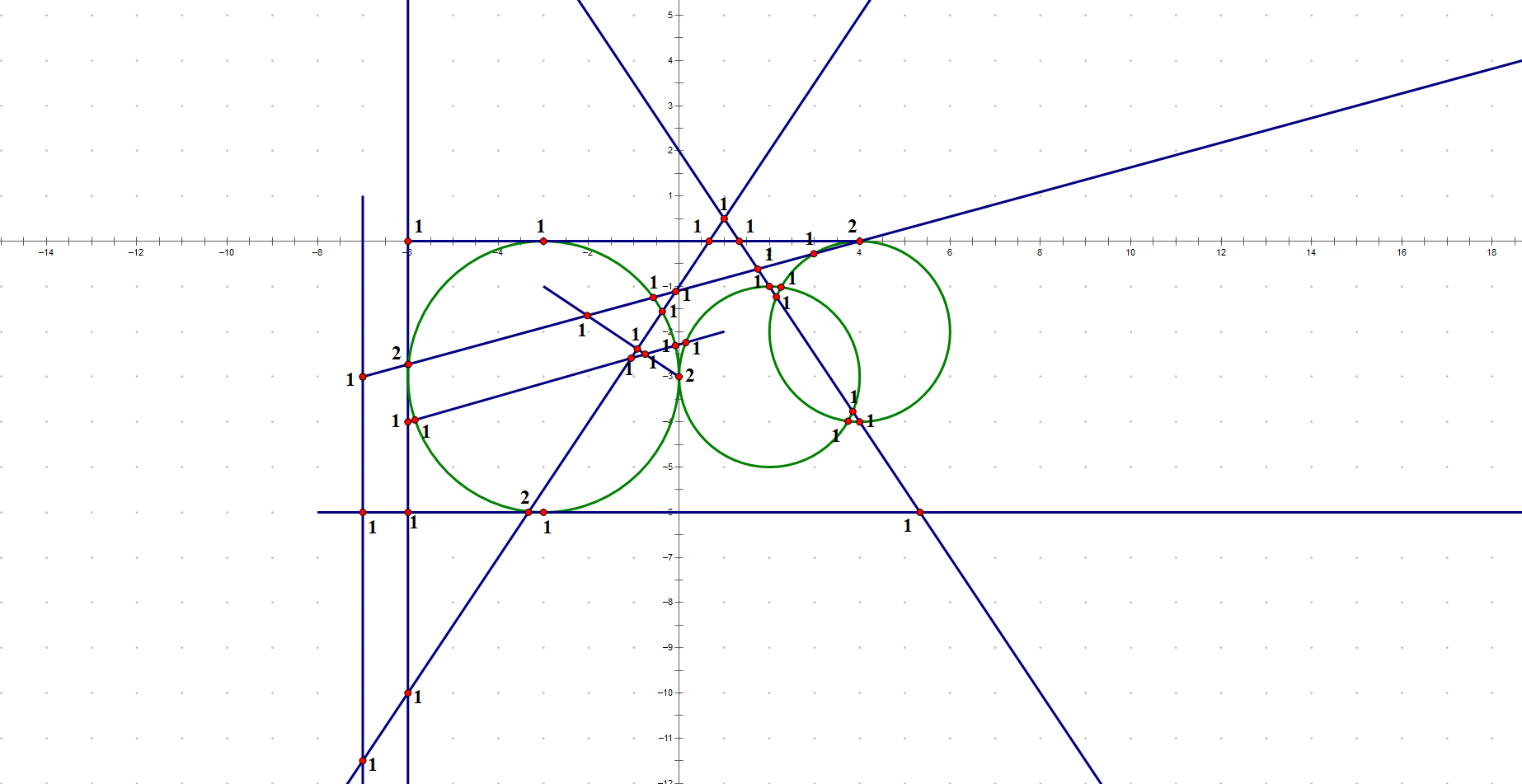
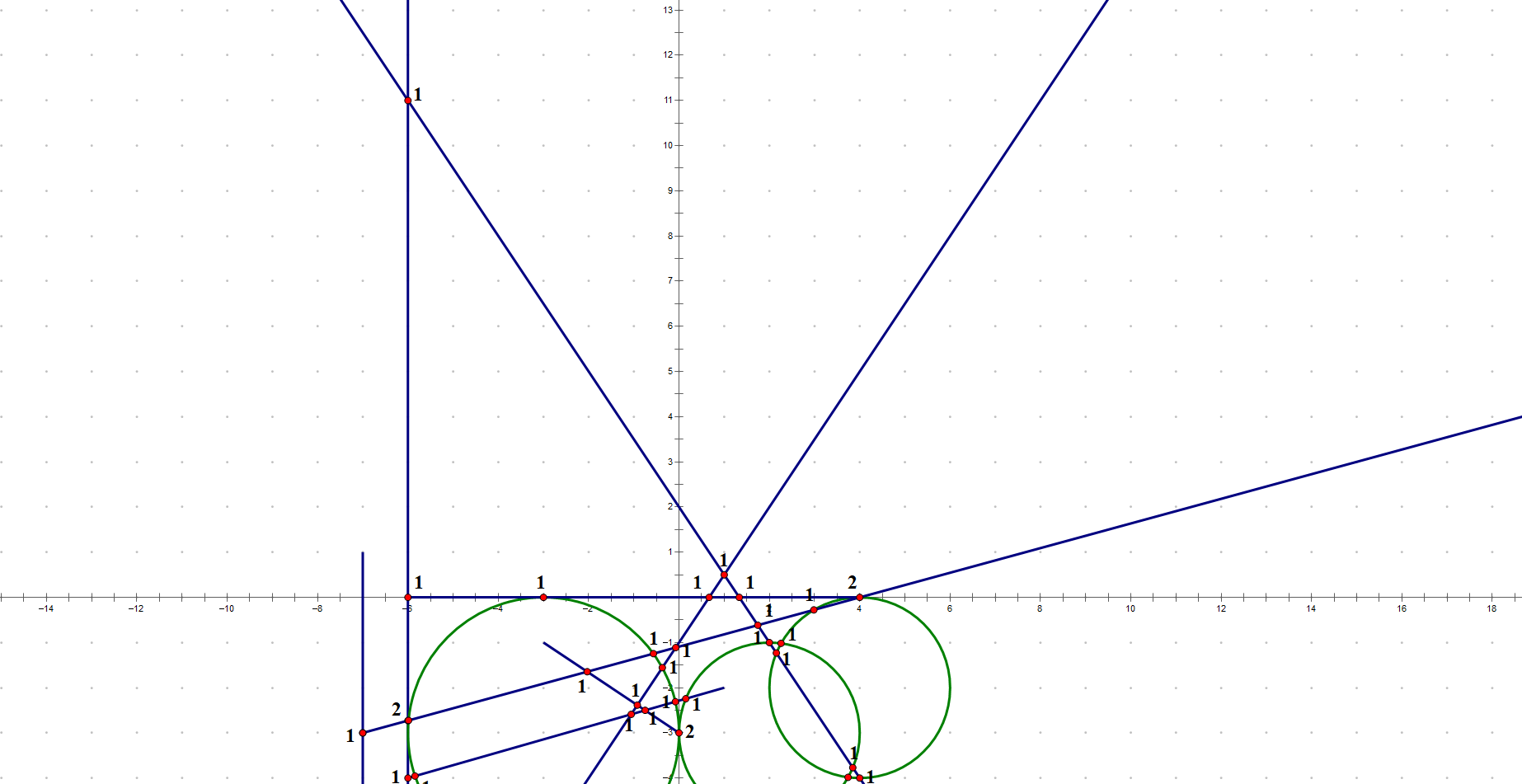
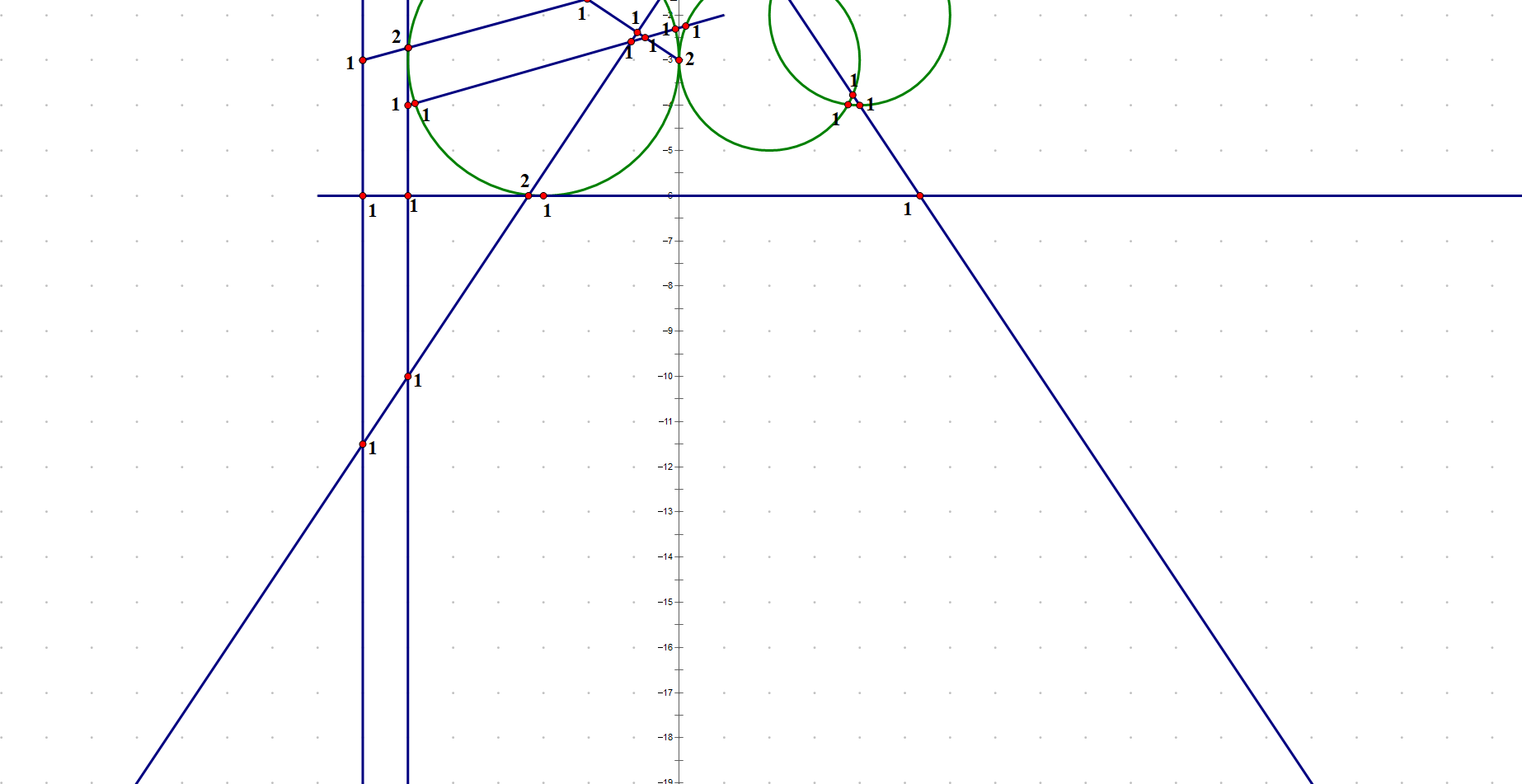
0 CNONE 1 SEGMENT (-3 , -1) (0 , -3) 3.60555 (0.83205 , -0.5547) 2 SEGMENT (-6 , 0) (4 , 0) 10 (1 , 0) 3 SEGMENT (-6 , -4) (1 , -2) 7.28011 (0.961524 , 0.274721) 4 RAY (-7 , 1) (0 , -1) 5 RAY (-7 , -3) (0.964764 , 0.263117) 6 RAY (-8 , -6) (1 , 0) 7 LINE (-4 , -7) (0.5547 , 0.83205) 8 LINE (-6 , -4) (0 , 1) 9 LINE (0 , 2) (0.5547 , -0.83205) 10 CIRCLE (-3 , -3) 3 11 CIRCLE (2 , -3) 2 12 CIRCLE (4 , -2) 2 ( -7 , -11.5 ) 4 7 INTX ( -7 , -6 ) 4 6 INTX ( -7 , -3 ) 4 5 INTX ( -6 , -10 ) 7 8 INTX ( -6 , -6 ) 6 8 INTX ( -6 , -4 ) 3 8 INTX ( -6 , -3 ) 8 10 INTX ( -6 , -2.72727 ) 5 8 INTX ( -6 , 0 ) 2 8 INTX ( -6 , 11 ) 8 9 INTX ( -5.98726 , -2.7238 ) 5 10 INTX ( -5.84381 , -3.95537 ) 3 10 INTX ( -3.33333 , -6 ) 6 7 INTX ( -3.32179 , -5.98269 ) 7 10 INTX ( -3 , -6 ) 6 10 INTX ( -3 , 0 ) 2 10 INTX ( -2.03226 , -1.64516 ) 1 5 INTX ( -1.05882 , -2.58824 ) 3 7 INTX ( -0.923077 , -2.38462 ) 1 7 INTX ( -0.75 , -2.5 ) 1 3 INTX ( -0.566588 , -1.24543 ) 5 10 INTX ( -0.370513 , -1.55577 ) 7 10 INTX ( -0.0807176 , -2.30878 ) 3 10 INTX ( -0.0740741 , -1.11111 ) 5 7 INTX ( 0 , -3 ) 1 11 INTX ( 0 , -3 ) 10 11 INTX ( 4.44089e-16 , -3 ) 1 10 INTX ( 0.148704 , -2.24323 ) 3 11 INTX ( 0.666667 , 0 ) 2 7 INTX ( 1 , 0.5 ) 7 9 INTX ( 1.33333 , 0 ) 2 9 INTX ( 1.74359 , -0.615385 ) 5 9 INTX ( 2 , -1 ) 9 11 INTX ( 2.15385 , -1.23077 ) 9 12 INTX ( 2.25838 , -3.98324 ) 11 12 INTX ( 2.98462 , -0.276923 ) 5 12 INTX ( 3.74162 , -1.01676 ) 11 12 INTX ( 3.84615 , -3.76923 ) 9 11 INTX ( 4 , -4 ) 9 12 INTX ( 4 , -1.77636e-15 ) 5 12 INTX ( 4 , 0 ) 2 5 INTX ( 4 , 0 ) 2 12 INTX ( 5.33333 , -6 ) 6 9 INTX 43 ( -7 , -11.5 ) 4 7 INTX ( -7 , -6 ) 4 6 INTX ( -7 , -3 ) 4 5 INTX ( -6 , -10 ) 7 8 INTX ( -6 , -6 ) 6 8 INTX ( -6 , -4 ) 3 8 INTX ( -6 , -3 ) 8 10 INTX ( -6 , -2.72727 ) 5 8 INTX ( -6 , 0 ) 2 8 INTX ( -6 , 11 ) 8 9 INTX ( -5.98726 , -2.7238 ) 5 10 INTX ( -5.84381 , -3.95537 ) 3 10 INTX ( -3.33333 , -6 ) 6 7 INTX ( -3.32179 , -5.98269 ) 7 10 INTX ( -3 , -6 ) 6 10 INTX ( -3 , 0 ) 2 10 INTX ( -2.03226 , -1.64516 ) 1 5 INTX ( -1.05882 , -2.58824 ) 3 7 INTX ( -0.923077 , -2.38462 ) 1 7 INTX ( -0.75 , -2.5 ) 1 3 INTX ( -0.566588 , -1.24543 ) 5 10 INTX ( -0.370513 , -1.55577 ) 7 10 INTX ( -0.0807176 , -2.30878 ) 3 10 INTX ( -0.0740741 , -1.11111 ) 5 7 INTX ( 4.44089e-16 , -3 ) 1 10 INTX ( 0 , -3 ) 1 11 INTX ( 0 , -3 ) 10 11 INTX ( 0.148704 , -2.24323 ) 3 11 INTX ( 0.666667 , 0 ) 2 7 INTX ( 1 , 0.5 ) 7 9 INTX ( 1.33333 , 0 ) 2 9 INTX ( 1.74359 , -0.615385 ) 5 9 INTX ( 2.15385 , -1.23077 ) 9 12 INTX ( 2.25838 , -3.98324 ) 11 12 INTX ( 2.98462 , -0.276923 ) 5 12 INTX ( 3.74162 , -1.01676 ) 11 12 INTX ( 3.84615 , -3.76923 ) 9 11 INTX ( 4 , 0 ) 2 5 INTX ( 4 , -4 ) 9 12 INTX ( 4 , 0 ) 2 12 INTX ( 4 , -1.77636e-15 ) 5 12 INTX ( 5.33333 , -6 ) 6 9 INTX 43 43





 浙公网安备 33010602011771号
浙公网安备 33010602011771号