CG2017 PA1-2 Segment Intersection Reporting (多线段求交)
Description (描述)
邓俊辉老师的学堂在线计算几何课堂第二章提到了Segment Intersection Reporting的BO算法,简单实现了一下。
Input (输入)
第一行 整数N,表示线段总数
后面N行,每行4个整数,格式为a,b,c,d,表示线段的起点(a,b)和终点(c,d),不保证起点在终点左边。
Output (输出)
输出所有交点的坐标及交点所在的两个线段,格式为
( a, b ) n1 n2
(a,b)是交点坐标,n1和n2是所在的线段编号
Sample Input (输入样例)
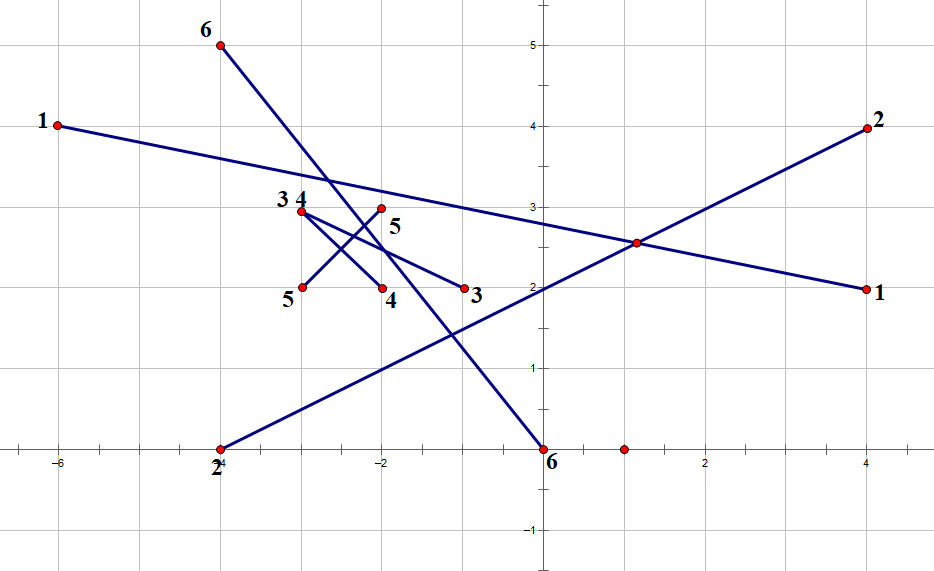
6 -6 4 4 2 -4 0 4 4 -3 3 -1 2 -3 3 -2 2 -3 2 -2 3 -4 5 0 0
Sample Output (输出样例)
/* ( -6 , 4 ) 1 LEFT 1 ( -4 , 0 ) 2 LEFT 2 1 ( -4 , 5 ) 6 LEFT 2 1 6 ( -3 , 2 ) 5 LEFT 2 5 1 6 ( -3 , 3 ) 3 LEFT 2 5 3 1 6 ( -3 , 3 ) 4 LEFT 2 5 4 3 1 6 ( -3 , 3 ) 0 INTX 2 5 4 3 1 6 ( -2.66667 , 3.33333 ) 0 INTX 2 5 4 3 6 1 ( -2.5 , 2.5 ) 0 INTX 2 4 5 3 6 1 ( -2.33333 , 2.66667 ) 0 INTX 2 4 3 5 6 1 ( -2.33333 , 2.66667 ) 0 INTX ( -2.22222 , 2.77778 ) 0 INTX 2 4 3 6 5 1 ( -2 , 2 ) 4 RIGHT 2 3 6 5 1 ( -2 , 2.5 ) 0 INTX 2 6 3 5 1 ( -2 , 2.5 ) 0 INTX ( -2 , 3 ) 5 RIGHT 2 6 3 1 ( -1 , 2 ) 3 RIGHT 2 6 1 ( 0 , 0 ) 6 RIGHT 2 1 ( 1.14286 , 2.57143 ) 0 INTX 1 2 ( 1.14286 , 2.57143 ) 0 INTX ( 4 , 2 ) 1 RIGHT 2 ( 4 , 4 ) 2 RIGHT */ ( -3 , 3 ) 4 3 ( -2.66667 , 3.33333 ) 1 6 ( -2.5 , 2.5 ) 5 4 ( -2.33333 , 2.66667 ) 5 3 ( -2.22222 , 2.77778 ) 5 6 ( -2 , 2.5 ) 3 6 ( 1.14286 , 2.57143 ) 2 1
Limitation (限制)
2 <= N <= 10^5
保证无竖直线段,保证线段间的交点只有一个
题解
按照邓老师课上讲的方法和数据结构,利用AVL存储当前状态,优先队列存储当前事件。
参考资料为
数据结构图文解析之:AVL树详解及C++模板实现 - 腾讯云开发者社区-腾讯云 (tencent.com)
二叉查找树的前驱后继 - 范仁义 - 博客园 (cnblogs.com)
#include<iostream>
#include<vector>
#include<algorithm>
#include<queue>
#include<set>
using namespace std;
#define EPS 1e-8
//#define DEBUG
enum TYPE{
NONE, LEFT, RIGHT, INTX
};
struct Point2{
double x;
double y;
// 点所在的线段编号
long long int n;
// 左右端点、或者交点
TYPE type;
// 交点所在的线段编号
long long int n1;
long long int n2;
Point2(double xx, double yy, long long int nn, TYPE e) : x(xx), y(yy), n(nn), type(e){
n1 = 0;
n2 = 0;
}
Point2() : x(0),y(0),n(0),type(NONE),n1(0),n2(0){}
bool operator== (const Point2& p) const{
return abs(x - p.x) < EPS && abs(y - p.y) < EPS && type == p.type && n == p.n && n1 == p.n1 && n2 == p.n2;
}
//需要最大堆,对小于号重载
bool operator < (const Point2& p) const{
return (x < p.x) || (abs(x - p.x) < EPS && (y < p.y || (abs(y - p.y) < EPS && (type < p.type || type == p.type && n < p.n))));
}
// 需要最小堆,对大于号重载
friend bool operator > (const Point2& p1, const Point2& p2) {
return (p1.x > p2.x) || (abs(p1.x - p2.x) < EPS && (p1.y > p2.y || (abs(p1.y - p2.y) < EPS && (p1.type > p2.type || (p1.type == p2.type && p1.n > p2.n)))));
}
friend ostream& operator<<(ostream& out, const Point2& p){
string str[] = {"NONE", "LEFT", "RIGHT", "INTX"};
out << "( " << p.x << " , " << p.y << " ) " << p.n << " " << str[p.type] << endl;
return out;
}
};
struct Segment
{
public:
Point2 p1;
Point2 p2;
long long int n;
double k;
Segment(){
p1 = Point2();
p2 = Point2();
k = 0;
n = 0;
};
Segment(Point2 pp1, Point2 pp2, long long int nn){
p1 = pp1;
p2 = pp2;
k = (pp2.y - pp1.y) / (pp2.x - pp1.x);
n = nn;
}
// j 是否在 i左边
bool toLeftTest(const Point2& s, const Point2& i, const Point2& j) const{
long long int x1 = i.x - s.x;
long long int x2 = j.x - s.x;
long long int y1 = i.y - s.y;
long long int y2 = j.y - s.y;
long long int res = x1 * y2 - x2 * y1;
//严格控制顶点不在线上
return res > 0;
}
bool isInSegment(const Segment& s) const{
auto xx = (k * p1.x - s.k * s.p1.x - p1.y + s.p1.y ) / (k - s.k);
return ((xx > p1.x || abs(xx - p1.x) < EPS) && (xx < p2.x || abs(xx - p2.x) < EPS)) &&
((xx > s.p1.x || abs(xx - s.p1.x) < EPS) && (xx < s.p2.x || abs(xx - s.p2.x) < EPS));
}
// 求出线段和扫描线的交点,方便判断
Point2 intersectionL(const double line) const{
return move(Point2(line, p1.y + k * (line - p1.x), n, NONE));
}
// 判断在 line这条扫描线上谁高谁底
bool lessS(const Segment& s, const double line){
auto pp1 = intersectionL(line);
auto pp2 = s.intersectionL(line);
// 处理相等的情况,按照线段后面的趋势来判断谁高谁底
if(abs(pp1.y - pp2.y) < EPS){
auto ppp1 = intersectionL(p2.x);
auto ppp2 = s.intersectionL(p2.x);
return ppp1.y < ppp2.y;
}
return pp1.y < pp2.y;
}
bool greaterS(const Segment& s, const double line){
auto pp1 = intersectionL(line);
auto pp2 = s.intersectionL(line);
if(abs(pp1.y - pp2.y) < EPS){
auto ppp1 = intersectionL(p2.x);
auto ppp2 = s.intersectionL(p2.x);
return ppp1.y > ppp2.y;
}
return pp1.y > pp2.y;
}
bool isIntersectionS(const Segment& s) const{
// 还要判断线段端点是否在别人的线上, 对于共线问题要特殊判断
if(isInSegment(s))
return true;
return (toLeftTest(p1, p2, s.p1) != toLeftTest(p1, p2, s.p2)) && (toLeftTest(s.p1, s.p2, p1) != toLeftTest(s.p1, s.p2, p2));
}
// 求出两个线段的交点
Point2 intersectionS(const Segment& s) {
auto res = Point2();
res.x = (k * p1.x - s.k * s.p1.x - p1.y + s.p1.y ) / (k - s.k);
res.y = p1.y + k * (res.x - p1.x);
// 在这里处理交点时,把低线段放在第一个
if(this->lessS(s, p1.x)){
res.n1 = n;
res.n2 = s.n;
}else{
res.n1 = s.n;
res.n2 = n;
}
res.type = TYPE::INTX;
res.n = 0;
return move(res);
}
bool operator == (const Segment& s){
return n == s.n;
}
friend ostream& operator<< (ostream& out, const Segment& s) {
out << s.n << endl;
return out;
}
};
struct AVLTreeNode
{
Segment key;
int height;
AVLTreeNode* left;
AVLTreeNode* right;
AVLTreeNode(Segment s, AVLTreeNode* l, AVLTreeNode* r) : key(s), left(l), right(r){}
~AVLTreeNode(){}
};
class AVLTree {
public:
AVLTreeNode* root;
AVLTree(){ root = nullptr;};
~AVLTree(){};
int getHeight(AVLTreeNode* p_root){
return !p_root? 0 : p_root->height;
}
void updateHeight(AVLTreeNode* p_root){
p_root->height = max(getHeight(p_root->left), getHeight(p_root->right)) + 1;
}
// 返回最大节点,最右节点最大
AVLTreeNode* maximum(AVLTreeNode* p_root) const {
if(p_root == nullptr) return nullptr;
while(p_root->right != nullptr) p_root = p_root->right;
return p_root;
}
// 返回最小节点,最左节点最小
AVLTreeNode* minimum(AVLTreeNode* p_root) const {
if(p_root == nullptr) return nullptr;
while(p_root->left != nullptr) p_root = p_root->left;
return p_root;
}
// 左单旋 : 在右子树插入右孩子
// 对节点y进行向左旋转操作,返回旋转后新的根节点x
// p_root x
// / \ / \
// T1 x 向左旋转 (p) p_root z
// / \ - - - - - - - -> / \ / \
// T2 z T1 T2 T3 T4
// / \
// T3 T4
AVLTreeNode* leftRotation(AVLTreeNode* p_root){
AVLTreeNode* pr_right = p_root->right;
p_root->right = pr_right->left;
pr_right->left = p_root;
// 注意是先更新子树,再更新根
updateHeight(p_root);
updateHeight(pr_right);
return pr_right;
}
// 右单旋 :在左子树插入左孩子
// 对节点y进行向右旋转操作,返回旋转后新的根节点x
// y x
// / \ / \
// x T4 向右旋转 (y) z y
// / \ - - - - - - - -> / \ / \
// z T3 T1 T2 T3 T4
// / \
// T1 T2
AVLTreeNode* rightRotation(AVLTreeNode* p_root){
AVLTreeNode* pr_left = p_root->left;
p_root->left = pr_left->right;
pr_left->right = p_root;
updateHeight(p_root);
updateHeight(pr_left);
return pr_left;
}
// 先右旋右子树再左旋根节点:在右子树插入左孩子
AVLTreeNode* rightLeftRotation(AVLTreeNode* p_root){
p_root->right = rightRotation(p_root->right);
return leftRotation(p_root);
}
// 先左旋左子树再右旋根节点:在左子树插入右孩子
AVLTreeNode* leftRightRotation(AVLTreeNode* p_root){
p_root->left = leftRotation(p_root->left);
return rightRotation(p_root);
}
AVLTreeNode* insert(AVLTreeNode* p_root, Segment& key, const double line){
if(p_root == nullptr){
p_root = new AVLTreeNode(key, nullptr, nullptr);
}
else if(key.greaterS(p_root->key, line)) { // 值比当前值大,在右子树插入
p_root->right = insert(p_root->right, key, line);
if(getHeight(p_root->right) - getHeight(p_root->left) == 2) //插入后失衡
{
if(key.greaterS(p_root->right->key, line)) // 插入右子树的右节点
p_root = leftRotation(p_root);
else if(key.lessS(p_root->right->key, line)) // 插入右子树的左节点
p_root = rightLeftRotation(p_root);
}
}
else if(key.lessS(p_root->key, line)) { // 值比当前值小,在左子树插入
p_root->left = insert(p_root->left, key, line);
if(getHeight(p_root->left) - getHeight(p_root->right) == 2) // 插入后失衡
{
if(key.lessS(p_root->left->key, line)) /// 插入左子树左节点
p_root = rightRotation(p_root);
else if(key.greaterS(p_root->left->key, line))
p_root = leftRightRotation(p_root);
}
}
updateHeight(p_root);
return p_root;
}
// 删除右子树节点相当于左子树加节点,造成失衡,反之亦然
AVLTreeNode* remove(AVLTreeNode*& p_root, Segment& key, const double line){
if(p_root == nullptr) return nullptr;
if(key == p_root->key){ // 找到删除节点
// 如果左右都不为空
if(p_root->left != nullptr && p_root->right != nullptr) {
if(getHeight(p_root->left) > getHeight(p_root->right)){ // 左子树比右子树高,在左子树寻找节点替换
AVLTreeNode* ppre = maximum(p_root->left); // 左子树最大节点
p_root->key = ppre->key; // 更换最大值
p_root->left = remove(p_root->left, ppre->key, line); // 递归删除最大节点
}else{
AVLTreeNode* psuc = minimum(p_root->right);
p_root->key = psuc->key;
p_root->right = remove(p_root->right, psuc->key, line);
}
}else{
AVLTreeNode* ptemp = p_root;
if(p_root->left != nullptr){ // 如果右空,返回左子树
p_root = p_root->left;
}else if(p_root->right != nullptr){ // 如果左空,返回右子树
p_root = p_root->right;
}else {
p_root = nullptr;
}
delete ptemp;
return p_root;
}
} else if(key.greaterS(p_root->key, line)){ // 在右子树删除
p_root->right = remove(p_root->right, key, line);
if(getHeight(p_root->left) - getHeight(p_root->right) == 2){
// 左子树插入右节点
if(getHeight(p_root->left->right) > getHeight(p_root->left->left))
p_root = leftRightRotation(p_root);
else
p_root = rightRotation(p_root);
}
} else if(key.lessS(p_root->key, line)){ // 在左子树删除
p_root->left = remove(p_root->left, key, line);
if(getHeight(p_root->right) - getHeight(p_root->left) == 2){
// 右子树插入左节点
if(getHeight(p_root->right->left) > getHeight(p_root->right->right))
p_root = rightLeftRotation(p_root);
else
p_root = leftRotation(p_root);
}
}
return p_root;
}
// 返回key值的node,同时通过指针返回该node的父节点
// 这里是要改变指针本身的值,而不是指针指向的对象,所以要加引用
AVLTreeNode* getNodeAndPrecParent(AVLTreeNode* p_root, const Segment& key, const double line, AVLTreeNode*& parent, AVLTreeNode*& firstParent){
while(p_root){
if(p_root->key == key) // 如果找到这个key对应的node返回该node,运行到这里时候parent已经被赋值了
return p_root;
parent = p_root; // 记录当前为Parent
if(p_root->key.greaterS(key, line))
p_root = p_root->left;
else{
firstParent = p_root; // 记录最近一个右拐的顶点
p_root = p_root->right;
}
}
return nullptr;
}
AVLTreeNode* precursor(AVLTreeNode* p_root, const Segment& key, const double line) {
if(p_root){
AVLTreeNode* parent = nullptr;
AVLTreeNode* firstParent = nullptr;
auto node = getNodeAndPrecParent(p_root, key, line, parent, firstParent);
if(node == nullptr)
return node;
if(node->left) // 有左子树
return maximum(node->left);
if(parent == nullptr || (parent && (nullptr == firstParent)))
return nullptr; // 没有前驱节点
if(node == parent->right)
return parent;
else
return firstParent;
}
return p_root;
}
// 返回key值的node,同时通过指针返回该node的父节点
AVLTreeNode* getNodeAndSuccParent(AVLTreeNode* p_root, const Segment& key, const double line, AVLTreeNode*& parent, AVLTreeNode*& firstParent){
while(p_root){
if(p_root->key == key)
return p_root;
parent = p_root;
if(p_root->key.lessS(key, line))
p_root = p_root->right;
else{
firstParent = p_root;
p_root = p_root->left;
}
}
return nullptr;
}
AVLTreeNode* succeed(AVLTreeNode* p_root, const Segment& key, const double line){
if(p_root){
AVLTreeNode* parent = nullptr;
AVLTreeNode* firstParent = nullptr;
auto node = getNodeAndSuccParent(p_root, key, line, parent, firstParent);
if(node == nullptr)
return node;
if(node->right)
return minimum(node->right);
if(parent == nullptr || (parent && (firstParent == nullptr)))
return nullptr;
if(node == parent->left)
return parent;
else
return firstParent;
}
return p_root;
}
// 遍历查找
AVLTreeNode* find(AVLTreeNode* p_root, const Segment& key, const double line){
if(p_root != nullptr) {
if(p_root->key == key)
return p_root;
auto l = find(p_root->left, key, line);
auto r = find(p_root->right, key, line);
if(l && l->key == key)
return l;
if(r && r->key == key)
return r;
}
return nullptr;
}
void inOrder(AVLTreeNode* p_root) const {
if(p_root != nullptr){
inOrder(p_root->left);
cout << p_root->key.n << " ";
inOrder(p_root->right);
}
}
void preOrder(AVLTreeNode* p_root) const {
if(p_root != nullptr){
cout << p_root->key.n << " ";
preOrder(p_root->left);
preOrder(p_root->right);
}
}
};
priority_queue<Point2, vector<Point2>, greater<Point2>> events;
vector<Segment> segments;
set<Point2> intxPoints;
AVLTree avl;
int N;
int main() {
cin >> N;
long long int a,b,c,d;
segments.push_back(Segment());
for(long long int i = 1; i <= N; i ++){
cin >> a >> b >> c >> d;
if(a < c) {
auto p1 = Point2(a, b, i, TYPE::LEFT);
auto p2 = Point2(c, d, i, TYPE::RIGHT);
events.push(p1);
events.push(p2);
segments.push_back(Segment(p1, p2, i));
}else{
auto p1 = Point2(a, b, i, TYPE::RIGHT);
auto p2 = Point2(c, d, i, TYPE::LEFT);
events.push(p1);
events.push(p2);
segments.push_back(Segment(p2, p1, i));
}
}
double L = 0;
while (!events.empty())
{
auto e = events.top();
events.pop();
cout << e;
L = e.x;
if(e.type == LEFT){
avl.root = avl.insert(avl.root, segments[e.n], L);
auto prec = avl.precursor(avl.root, segments[e.n], L);
auto succ = avl.succeed(avl.root, segments[e.n], L);
if(prec && segments[e.n].isIntersectionS(prec->key)) {
auto p = segments[e.n].intersectionS(prec->key);
// 需要交点在L之后才加入队列,防止重复探测造成 INTX 重复,而导致错误交换seg顺序
if(p.x > L || abs(p.x - L) < EPS)
events.push(p);
}
if(succ && segments[e.n].isIntersectionS(succ->key)) {
auto p = segments[e.n].intersectionS(succ->key);
if(p.x > L || abs(p.x - L) < EPS)
events.push(p);
}
avl.inOrder(avl.root);
cout << endl;
}else if(e.type == RIGHT){
auto prec = avl.precursor(avl.root, segments[e.n], L);
auto succ = avl.succeed(avl.root, segments[e.n], L);
if(prec && succ && prec->key.isIntersectionS(succ->key)){
auto p = prec->key.intersectionS(succ->key);
if(p.x > L || abs(p.x - L) < EPS)
events.push(p);
}
avl.root = avl.remove(avl.root, segments[e.n], L);
avl.inOrder(avl.root);
cout << endl;
}else if(e.type == INTX){
//cout << " ( " << e.x << " , " << e.y << " ) " << e.n1 << " " << e.n2 << endl;
// 防止多次判断同一对线段的交点,从而错误的改变该线段的次序
if(intxPoints.find(e) == intxPoints.end())
intxPoints.insert(e);
else
continue;
// 此时 e.n1比e.n2低 ,因此找e.n2的后继和e.n1的前驱,交换后重新判断
auto prec = avl.precursor(avl.root, segments[e.n1], L);
auto succ = avl.succeed(avl.root, segments[e.n2], L);
// 但是在交点的横坐标L处,n1和n2实际上用作排序的值已经相等了,想不到什么O(logn)的查找方法,直接遍历吧
// 或许就是在判断相等的时候,用左端点所在的垂直线判断,这个就不写了,直接遍历完事
auto s1 = avl.find(avl.root, segments[e.n1], L);
auto s2 = avl.find(avl.root, segments[e.n2], L);
// swap,当前走向是 n1 低于 n2,如果未来是n2 低于 n1的话,再交换
if(s1->key.greaterS(s2->key, s1->key.p2.x)){
auto tmp = s1->key;
s1->key = s2->key;
s2->key = tmp;
}
if(prec && segments[e.n2].isIntersectionS(prec->key)) {
auto p = segments[e.n2].intersectionS(prec->key);
if(p.x > L || abs(p.x - L) < EPS)
events.push(p);
}
if(succ && segments[e.n1].isIntersectionS(succ->key)) {
auto p = segments[e.n1].intersectionS(succ->key);
if(p.x > L || abs(p.x - L) < EPS)
events.push(p);
}
avl.inOrder(avl.root);
cout << endl;
}
}
for(auto e : intxPoints)
cout << " ( " << e.x << " , " << e.y << " ) " << e.n1 << " " << e.n2 << endl;
return 0;
}
思考不周嗯写的代码,如有纰漏,欢迎指正!!!
————————————————————————————————————————————华丽的分割线 20221028
Tsinghua computing geometry assignment: CG2017 PA1-2 Crossroad (architecture.pub)
从这个新的参考资料中了解到,如果新增加了圆,可以把圆拆成四段圆弧,再放进上述算法中进行相交求解,此时需要增加Segment的类型,有line和circle,如果是两个相同编号的circle相交,不计入交点。
对于射线和直线,则通过window box进行裁剪,将射线和直线转换成window box内的线段,再利用上述算法求解





 浙公网安备 33010602011771号
浙公网安备 33010602011771号