CG2017 PA1-1 Convex Hull (凸包)
Description (描述)
After learning Chapter 1, you must have mastered the convex hull very well. Yes, convex hull is at the kernel of computational geometry and serves as a fundamental geometric structure. That's why you are asked to implement such an algorithm as your first programming assignments.
Specifically, given a set of points in the plane, please construct the convex hull and output an encoded description of all the extreme points.
经过了第一章的学习,想必你对于凸包的认识已经非常深刻。是的,凸包是计算几何的核心问题,也是一种基础性的几何结构。因此你的第一项编程任务,就是来实现这样的一个算法。
具体地,对于平面上的任意一组点,请构造出对应的凸包,并在经过编码转换之后输出所有极点的信息。
Input (输入)
The first line is an integer n > 0, i.e., the total number of input points.
The k-th of the following n lines gives the k-th point:
pk = (xk, yk), k = 1, 2, ..., n
Both xk and yk here are integers and they are delimited by a space.
第一行是一个正整数首行为一个正整数n > 0,即输入点的总数。
随后n行中的第k行给出第k个点:
pk = (xk, yk), k = 1, 2, ..., n
这里,xk与yk均为整数,且二者之间以空格分隔。
Output (输出)
Let { s1, s2, ..., sh } be the indices of all the extreme points, h ≤ n. Output the following integer as your solution:
( s1 * s2 * s3 * ... * sh * h ) mod (n + 1)
若 { s1, s2, ..., sh } 为所有极点的编号, h ≤ n,则作为你的解答,请输出以下整数:
( s1 * s2 * s3 * ... * sh * h ) mod (n + 1)
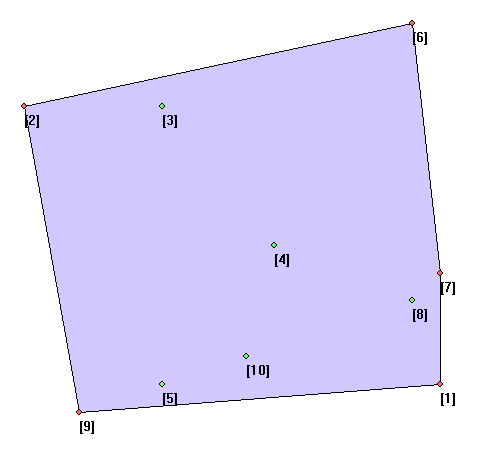
Sample Input (输入样例)
10
7 9
-8 -1
-3 -1
1 4
-3 9
6 -4
7 5
6 6
-6 10
0 8

Sample Output (输出样例)
7 // ( 9 x 2 x 6 x 7 x 1 x 5 ) % (10 + 1)
Limitation (限制)
- 3 ≤ n ≤ 10^5
- Each coordinate of the points is an integer from (-10^5, 10^5). There are no duplicated points. Each point is selected uniformly randomly in (-10^5, 10^5) x (-10^5, 10^5).
- All points on extreme edges are regarded as extreme points and hence should be included in your solution.
- Time Limit: 2 sec
- Space Limit: 512 MB
- 3 ≤ n ≤ 10^5
- 所有点的坐标均为范围(-10^5, 10^5)内的整数,且没有重合点。每个点在(-10^5, 10^5) x (-10^5, 10^5)范围内均匀随机选取
- 极边上的所有点均被视作极点,故在输出时亦不得遗漏
- 时间限制:2 sec
- 空间限制:512 MB
Hint (提示)
Use the CH algorithms presented in the lectures.
课程中讲解过的凸包算法
题解
使用课程中介绍的Graham Scan算法。
在预处理的极角排序部分,分三步:第一步找出Lowest than leftest点;第二步对所有点以LTL为极点进行极角排序,此时若共线取最小距离点优先;第三步,对拥有最大极角的所有共线的点进行排序,此时取最大距离点优先。
最后直接进行Graham Scan算法即可。
注意数据范围是10^5,乘法容易爆int,用long long即可。
如要优化效率,可以开数组去存储下标、XY坐标,手撕nlogn的排序,利用int S 和int T作为索引,在排好序的下标数组上模拟栈的运行即可。
#include<iostream>
#include<vector>
#include<algorithm>
using namespace std;
//#define DEBUG
struct Point2{
long long int x;
long long int y;
long long int n;
Point2(long long int xx, long long int yy, long long int nn) : x(xx), y(yy), n(nn){}
Point2(){
x = 0;
y = 0;
n = 0;
}
bool operator== (const Point2& p) const{
return x == p.x && y == p.y;
}
};
int N;
vector<Point2> points;
Point2 LTL; // lowest than leftest
// 用来做初始极角排序的toLeftTest,当共线时返回距离近的
bool toLeftTest(const Point2& s, const Point2& i, const Point2& j){
long long int x1 = i.x - s.x;
long long int x2 = j.x - s.x;
long long int y1 = i.y - s.y;
long long int y2 = j.y - s.y;
long long int res = x1 * y2 - x2 * y1;
// 共线的情况,返回距离近的
if(res == 0)
return x1 * x1 + y1 * y1 < x2 * x2 + y2 * y2;
return res > 0;
}
// 用来对最大极角上共线的点做排序的toLeftTest,当共线时返回距离远的
bool toLeftTest2(const Point2& s, const Point2& i, const Point2& j){
long long int x1 = i.x - s.x;
long long int x2 = j.x - s.x;
long long int y1 = i.y - s.y;
long long int y2 = j.y - s.y;
long long int res = x1 * y2 - x2 * y1;
// 共线的情况,返回距离远的
if(res == 0)
return x1 * x1 + y1 * y1 > x2 * x2 + y2 * y2;
return res > 0;
}
// 用来进行graham scan算法的toLeftTest,当共线时也返回true
bool gToLeftTest(const Point2& s, const Point2& i, const Point2& j){
long long int x1 = i.x - s.x;
long long int x2 = j.x - s.x;
long long int y1 = i.y - s.y;
long long int y2 = j.y - s.y;
long long int res = x1 * y2 - x2 * y1;
return res >= 0;
}
int main(){
cin >> N;
long long int idx = 0;
for(long long int i = 0; i < N; i ++){
long long int x, y;
cin >> x >> y;
points.emplace_back(Point2(x, y, i + 1));
if(points[i].y < points[idx].y){
idx = i;
}else if(points[i].y == points[idx].y){
if(points[i].x < points[idx].x){
idx = i;
}
}
}
LTL = points[idx];
auto cmp = [](const Point2& p1, const Point2&p2){
return (p1 == LTL) || (!(p2 == LTL) && toLeftTest(LTL, p1, p2));
};
sort(points.begin(), points.end(), cmp);
#ifdef DEBUG
for(auto p : points){
cout << p.n << " " << p.x << " " << p.y << endl;
}
cout << endl;
#endif
// 找出与最大极角共线的距离极点最小的点,确定二次排序范围
long long int nIdx = 0;
for(long long int i = N - 1; i > 0; i --){
Point2& p1 = points[i];
Point2& p2 = points[N - 1];
long long int x1 = p1.x - LTL.x;
long long int x2 = p2.x - LTL.x;
long long int y1 = p1.y - LTL.y;
long long int y2 = p2.y - LTL.y;
int res = x1 * y2 - x2 * y1;
if(res != 0){
nIdx = i;
break;
}
}
#ifdef DEBUG
cout << nIdx << endl;
#endif
auto cmp2 = [](const Point2& p1, const Point2&p2){
return toLeftTest2(LTL, p1, p2);
};
sort(points.begin() + nIdx + 1, points.end(), cmp2);
#ifdef DEBUG
for(auto p : points){
cout << p.n << " " << p.x << " " << p.y << endl;
}
cout << endl;
#endif
// graham scan
/*
int S = 1;
int T = 2;
while (T < N)
{
if(gToLeftTest(points[S - 1], points[S], points[T])){
points[++S] = points[T++];
}else{
--S;
}
}*/
vector<Point2> S, T;
S.push_back(points[0]);
S.push_back(points[1]);
for(long long int i = points.size() - 1; i > 1; i --)T.push_back(points[i]);
while (!T.empty())
{
if(gToLeftTest(S[S.size()-2], S[S.size()-1], T[T.size() - 1])){
S.push_back(T[T.size() - 1]);
T.pop_back();
}else{
S.pop_back();
}
}
long long int res = 1;
//for(int i = 0; i <= S; i ++) {
// Point2& p = points[i];
for(auto p : S){
#ifdef DEBUG
cout << p.n << " " << p.x << " " << p.y << endl;
#endif
res = ((res % (N + 1)) * (p.n % (N + 1))) % (N+1);
}
//res = ((res % (N + 1)) * ((S + 1) % (N + 1))) % (N+1);
res = ((res % (N + 1)) * ((S.size()) % (N + 1))) % (N+1);
cout << res;
return 0;
}
得分:100
未考虑效率,可优化空间很大。





 浙公网安备 33010602011771号
浙公网安备 33010602011771号