【K-D Tree】BZOJ_4303 数列

题意

给出\(n\)个数，每个数有一个标号和标识符。
有\(m\)个询问，每次以标号或标识符为下标进行区间操作。
\(1 \leq n,m \leq 50000\)。

思路

标号和标识符即这个元素的二维上的信息。
用\(K-D\ Tree\)可以轻松处理。
具体地，交替地以\(x\)轴或\(y\)轴进行划分。
贴几个例子，

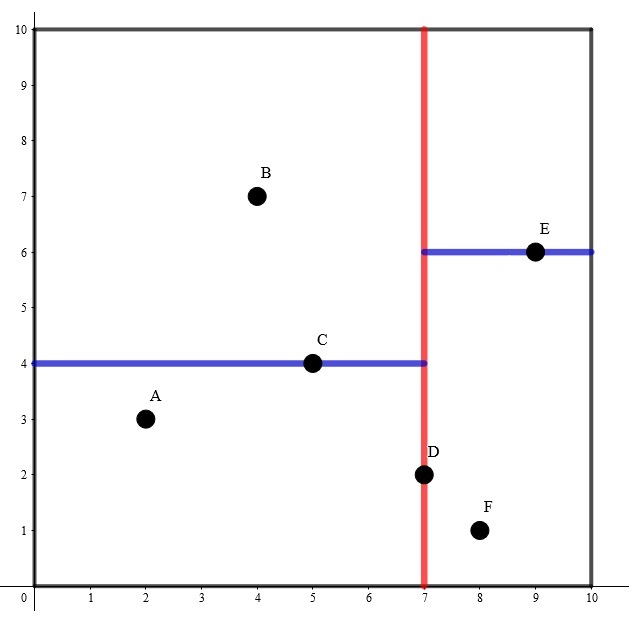
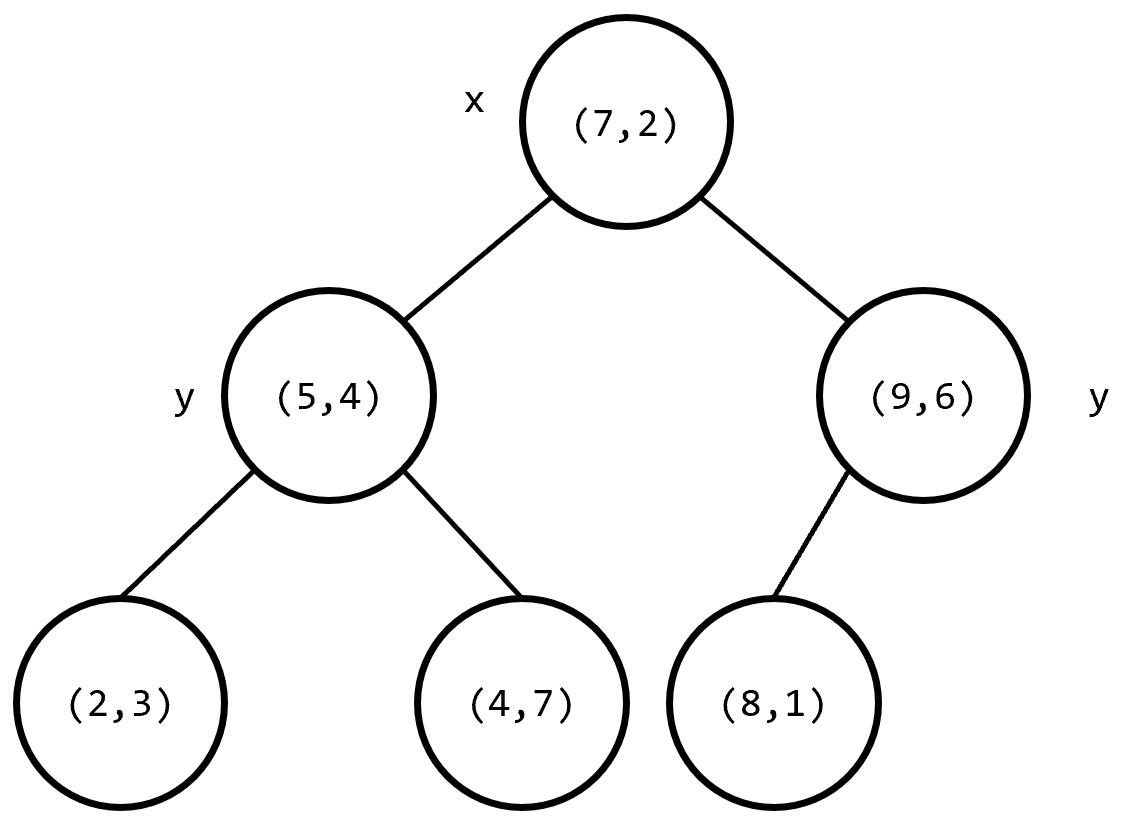
代码

#pragma GCC optimize(2)
#pragma GCC optimize("Ofast")
#include <cctype>
#include <cstdio>
#include <algorithm>
#define int long long
#define getchar() (p1 == p2 && (p2 = (p1 = buf) + fread(buf, 1, 1 << 21, stdin), p1 == p2) ? EOF : *p1++)


const int mod = 536870912;
int Dimen, n, m, rt;
char buf[1 << 23], *p1 = buf, *p2 = buf, obuf[1 << 23], *O = obuf;

inline int read() {
	int res = 0, f = 1;
	char c = getchar();
	while (!isdigit(c)) {
		if (c == '-') f = -1;
		c = getchar();
	}
	while (isdigit(c))
		res = res * 10 + (c ^ 48), c = getchar();
	return res * f;
}

struct kdTree {
	int tp, ls, rs, val;
	int pls, mlt, sum, len;
	int v[2], mx[2], mi[2];//记录当前点的坐标及儿子们的坐标范围 
	bool operator < (const kdTree &y) const {
        return v[Dimen] < y.v[Dimen];
    }
} tree[50001];

void update(int p) {
	int ls = tree[p].ls, rs = tree[p].rs;
	tree[p].mx[0] = std::max(tree[p].v[0], std::max(tree[ls].mx[0], tree[rs].mx[0]));
	tree[p].mx[1] = std::max(tree[p].v[1], std::max(tree[ls].mx[1], tree[rs].mx[1]));
	tree[p].mi[0] = std::min(tree[p].v[0], std::min(tree[ls].mi[0], tree[rs].mi[0]));
	tree[p].mi[1] = std::min(tree[p].v[1], std::min(tree[ls].mi[1], tree[rs].mi[1]));
}

int build(int l, int r, int dimen) {//
	Dimen = dimen;
	int mid = l + r >> 1, p = mid;
	std::nth_element(tree + l, tree + mid, tree + r + 1);
	//tree[mid]上为tree[l~r]的中位数
	tree[p].tp = Dimen;
	tree[p].mlt = 1;
	tree[p].len = r - l + 1;
	if (l < mid)
		tree[p].ls = build(l, mid - 1, dimen ^ 1);
	if (r > mid)
		tree[p].rs = build(mid + 1, r, dimen ^ 1);
	update(p);//!!
	return p;
}

void addMlt(int p, int v) {
	(tree[p].mlt *= v) %= mod;
	(tree[p].pls *= v) %= mod;
	(tree[p].val *= v) %= mod;
	(tree[p].sum *= v) %= mod;
}

void addPls(int p, int v) {
	(tree[p].pls += v) %= mod;
	(tree[p].val += v) %= mod;
	(tree[p].sum += v * tree[p].len) %= mod;
}

void spread(int p) {
	int ls = tree[p].ls, rs = tree[p].rs;
	if (tree[p].mlt != 1) {
		addMlt(ls, tree[p].mlt);
		addMlt(rs, tree[p].mlt);
		tree[p].mlt = 1;
	}
	if (tree[p].pls) {
		addPls(ls, tree[p].pls);
		addPls(rs, tree[p].pls);
		tree[p].pls = 0;
	}
}

void modify(int p, int l, int r, int mlt, int pls) {
	if (tree[p].mx[Dimen] < l || tree[p].mi[Dimen] > r)
		return;
	if (l <= tree[p].mi[Dimen] && tree[p].mx[Dimen] <= r) {
		addMlt(p, mlt);
		addPls(p, pls);
		return;
	}
	spread(p);
	if (l <= tree[p].v[Dimen] && tree[p].v[Dimen] <= r)
		tree[p].val = (tree[p].val * mlt + pls) % mod;
	modify(tree[p].ls, l, r, mlt, pls);
	modify(tree[p].rs, l, r, mlt, pls);
	tree[p].sum = (tree[p].val + tree[tree[p].ls].sum + tree[tree[p].rs].sum) % mod;
}

int query(int p, int l, int r) {
	if (tree[p].mx[Dimen] < l || tree[p].mi[Dimen] > r)
		return 0;
	if (l <= tree[p].mi[Dimen] && tree[p].mx[Dimen] <= r)
		return tree[p].sum;
	spread(p);
	int res = 0;
	if (l <= tree[p].v[Dimen] && tree[p].v[Dimen] <= r)
		res = tree[p].val;
	return (res + query(tree[p].ls, l, r) + query(tree[p].rs, l, r)) % mod;
}

signed main() {
	freopen("sequence.in", "r", stdin);
	freopen("sequence.out", "w", stdout);
	n = read(), m = read();
	tree[0].mx[0] = tree[0].mx[1] = -0x3f3f3f3f;
	tree[0].mi[0] = tree[0].mi[1] = 0x3f3f3f3f;//在建树之前就要操作，不然到0时mx和mi会更新错误
	for (int i = 1; i <= n; i++)
		tree[i].v[0] = i, tree[i].v[1] = read();
	rt = build(1, n, 0);
	for (int i = 1, opt, l, r, x, y; i <= m; i++) {
		opt = read();
		if (opt < 2) {
			Dimen = opt;
			l = read(), r = read(), x = read(), y = read();
			modify(rt, l, r, x, y);
		} else {
			Dimen = opt - 2;
			l = read(), r = read();
			printf("%lld\n", query(rt, l, r) % mod);
		}
	}
}