初赛整理

基础知识

• 1（位）字节(Byte)=8比特(bit)

• Linux下可执行文件的默认扩展名 不需要

• 提出“存储程序”的计算机工作原理的是 冯•诺依曼

• 前缀表达式：从右往左，如果当前字符(或字符串)为数字或 变量，则压入栈内；如果是 运算符，则将栈顶两个元素弹出栈外并作相应运算，再将结果压入栈内
  后缀表达式：从左往右，。。。

• NOI 1984年

• 二进制哈夫曼编码进行压缩
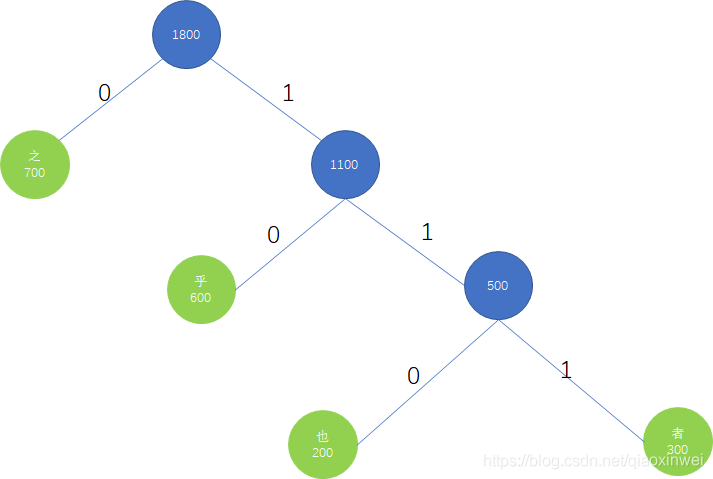
  如图，类似合并果子地建树。

• 阶码、尾数：
  1、阶码指明了小数点在数据中的位置
  2、阶码位数越多，可表示的数的范围越大；
  3、尾数越多，所表示的数的精度越高。

• 如果根结点的深度记为1，则一棵恰有2011个叶子结点的二叉树的深度可能是（CD）。
  A．10 B．11 C．12 D．2011
  很考察审题的一道题，审题店是“叶子结点”，度为0的点为叶子结点（没有子节点的点），由于一层最多容纳2^(n-1)个叶子结点，所以至少12层。

• 原码、反码、补码：

1. 原码
   原码就是符号位加上真值的绝对值, 即用第一位表示符号, 其余位表示值.
2. 反码
   反码的表示方法是:
   正数的反码是其本身
   负数的反码是在其原码的基础上, 符号位不变，其余各个位取反.
3. 补码
   补码的表示方法是:
   正数的补码就是其本身
   负数的补码是在其原码的基础上, 符号位不变, 其余各位取反, 最后+1. (即在反码的基础上+1)

• 整数的补码表示法：补码特性：正0和负0表示相同

• 排序
  堆排序、快速排序、希尔排序、直接选择排序是不稳定的排序算法；
  冒泡排序、直接插入排序、折半插入排序、归并排序是稳定的排序算法。

• 主定理
  

问题求解

排列组合

Catalan数列：

\[H_n=\frac{\binom{2n}{n}}{n+1} \]

可以算出以下问题的方案数：
表示通过连接顶点而将\(n + 2\)边的凸多边形分成三角形的方法个数。
表示长度为\(n\)的入栈序列对应的合法出栈序列个数。

排列组合解题技巧
插入法：要求不相邻。先排好别的再插入。
捆绑法：将需要排在一起的元素捆绑在一起。
剩余法：取法和剩法对应。
对等法：限制条件的肯定与否定对等，那么就各占总方案的一半。
排异法：容斥，总方案-不合法方案。

圆排列：
从n个不同元素中取r个元素的圆排列：

\[\frac{P_{n}^{r}}{r} \]

n个元素的圆排列：

\[\frac{P_{n}^{n}}{n}=(n-1)! \]

错排公式：

\[f_n=(n-1)*(f_{n-1}+f_{n-2})，f_1=0;f_2=1; \]

\[f_n=n!\sum_{i=1}^{n}(-1)^i\frac{1}{i}(容斥原理，至少有i个位置上不合法的个数为(n-i)!，减去即可) \]

递推分两步：
第一步，把第n个元素放在一个位置，比如位置k，一共有n-1种方法；
第二步，放编号为k的元素，这时有两种情况：
⑴把它放到位置n，那么，对于剩下的n-1个元素，由于第k个元素放到了位置n，剩下n-2个元素就有D(n-2)种方法；
⑵第k个元素不把它放到位置n，这时，对于这n-1个元素，有D(n-1)种方法；
还有一个很酷的公式\(f_n=[\frac{n!}{e}+0.5]\)

第二类Stirling数
\(n\)个有区别的球放到\(m\)个相同的盒子中，要求无一空盒，其不同的方案数用\(S(n,m)\)表示，称为第二类Stirling数

\(S(n,m)=m*S(n-1,m)+S(n-1,m-1) (n>1,m>1)\)（新加的第n个球，可以独占一个盒子，也可以和别的球放在一起）
边界条件：S(n,1)=1；S(n,n)=1；S(n,k)=0(k>n)

设\(f(n,k)\)是从集合\({1，2，\cdots，n}\)中能够选择的没有两个连续整数的\(k\)个元素子集的数目，求递归式\(f(n,k)\)。

所以：\(f(n,k)=f(n-2,k-1)+f(n-1,k)\)
边界条件：\(f(n,1)=n, f(n,k)=0(n<=k)\)
（分\(n\)取或不取的情况）

整数划分：
将整数\(n\)分成\(k\)份，且每份不能为空（不考虑顺序）。

用\(f_{i,j}\)表示将整数\(i\)分成\(j\)份的分法
分两类情况：
存在1的情况，\(f_{i,j}=f_{i-1,j-1}\)
不存在1的情况，\(f_{i,j}=f_{i-j,j}\)，即在\(f_{i-1,j}\)的每一份上+1

这里存在1与不存在1是两种对立的情况，而在不存在1的情况中，\(f_{i-1,j}\)的方案是不同的，故每一份加上1也是不同的。
所以\(f_{i,j}=f_{i-1,j-1}+f_{i-1,j}\)。

一些题目

• 记T为一队列,初始时为空,现有n个总和不超过32的正整数依次入列.如果无论这些数具体为何值,都能找到一种出队的方式,使得存在某个时刻队列T中的数之和恰好为9,那么n的最小值是___________.
  本题可用抽屉原理求解.
  设 为各正整数值,则T的队列顺序为 a1,a2,a3… an,设bi为前i项数之和,则 b0=0,b1=a1 ,b2=a1+a2 ,b3=a1+a2+a3 ….如队列T中的数之和恰好为9,实际上即是找到某个bj和bi ,使得 bj-bi=9.由题意可知bi取值范围为1-32,现将这32个数构造为集合{1,10}, {2,11}, …, {8,17}, {18,27}, {19,28},…,{23,32} ,{24},{25},{26},这17个集合中的任一个集合不能包含两个或两个以上的 ,否则它们的差为9.例如设n=17时,队列T为 11111111 10 11111111,即 b1=1, b2 =2,… b8=8, b9 =18, b10=19, b11=20… b17=26,它们中没有任意两个数是在同一集合内的,所以不存在数之和恰好等于9.
  故根据抽屉原理可得,当n=18时,至少存在两个 在同一个集合,即它们的差为9.
  因此,答案为n=18.

• 牛马期望题与牛马的我
  假设一台抽奖机中有红、蓝两色的球，任意时刻按下抽奖按钮，都会等概率
  获得红球或蓝球之一。有足够多的人每人都用这台抽奖机抽奖，假如他们的
  策略均为：抽中蓝球则继续抽球，抽中红球则停止。最后每个人都把自己获
  得的所有球放到一个大箱子里，最终大箱子里的红球与蓝球的比例接近于
  设一个人\(E\)为拿到蓝球的期望个数，有\(E=\frac{1}{2}(E+1)\)，解得\(E=1\)，所以比例接近于\(1:1\)。
  期望公式\(E=\sum p(X_i)X_i\)。将题目代入，分为拿红蓝两种情况，拿蓝的话概率为1/2，对答案贡献为E+1，拿红的话概率也为1/2，但是因为停止了游戏，所以贡献为0。

题目：
书架上有21本书，编号从1到21，从其中选4本，其中每两本的编号都不相邻的选法一共有______种。

选出4本=放入4本，这就要求放入的书不相邻，即只能从17本书的间隔挑4个空放入，答案为\(C_{21-4+1}^{4}\)

题目：
由3个a，5个b和2个c构成的所有字符串中，包含子串“abc”的共有（ ）个。

可以看成有1个abc，2个a，4个b，1个c的全排列个数

\[\frac{(1+2+4+1)!}{1!2!4!1!} \]

还存在有2个abc的方案被算了两次，即2个abc，1个a，3个b的全排列个数

\[\frac{(2+1+3)!}{2!1!3!} \]

也可以先把1个字母的排好，再插入abc，不过不要漏了2个abc排在一起的情况。