【GDOI 2016 Day1】第二题 最长公共子串

题面

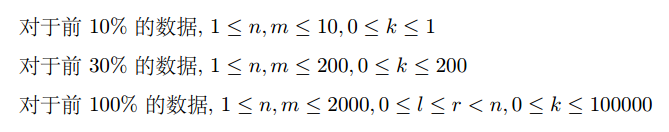
题意

求\(S\)串和\(T\)串的最长公共子串。不同的是\(S\)串中有\(k\)个区间的字母可以重排，且不限重排次数。

思路

容易发现可以重排的区间交叉可以合并，这样最多有2000个区间。
然后dp。
设\(f_{i,j}\)为以\(S\)串的第\(i\)个区间开头，以\(T\)串的第\(j\)个字母开头的最长公共子串。
对于区间\(i\)，判断是否可以与\([j\sim j+len)\)匹配。
如果全部匹配，则\(f_{i,j}=len+f_{i+1,j+len}\)（即可以与\(i+1\)的区间接上）；
否则\(f_{i,j}=len\)（无法接上）。
另外对于左边，可能有部分的子串可以匹配，暴力判断即可。

代码

#include <cstdio>
#include <cstring>
#include <algorithm>

struct node {
	int l, r, len;
}a[100002], b[2001];

int m, n, k, cnt, ans;
int f[2001][2001], pre[2001][27], tmp[27];
char t[2001], s[2001];

bool cmp(node x, node y) {
	return x.l == y.l ? x.r > y.r : x.l < y.l;
}

int main() {
	freopen("lcs.in", "r", stdin);
	freopen("lcs.out", "w", stdout);
	scanf("%s", t + 1);
	scanf("%s", s + 1);
	m = strlen(t + 1);
	n = strlen(s + 1);
	scanf("%d", &k);
	for (int i = 1; i <= k; i++)
		scanf("%d %d", &a[i].l, &a[i].r), a[i].l++, a[i].r++;
	std::sort(a + 1, a + k + 1, cmp);
	a[k + 1] = (node){n + 1};
	int st = a[1].l, ed = a[1].r;
	for (int i = 1; i < st; i++)
		b[++cnt] = (node){i, i, 1};
	for (int i = 1; i <= k + 1; i++)
		if (a[i].l <= ed)
			ed = std::max(ed, a[i].r);
		else {
			b[++cnt] = (node){st, ed, ed - st + 1}, st = a[i].l, ed = a[i].r;
			for (int j = b[cnt].r + 1; j < a[i].l; j++)
				b[++cnt] = (node){j, j, 1};
		}
	for (int i = 1; i <= n; i++) {
		pre[i][s[i] - 96]++;
		for (int j = 1; j <= 26; j++)
			pre[i][j] += pre[i - 1][j];
	}
	int flag;
	for (int i = cnt; i >= 1; i--) 
		for (int j = m; j >= 1; j--) {
			memset(tmp, 0, sizeof(tmp));
			flag = 0;
			for (int l = j; l < j + b[i].len && l <= m; l++) {
				if (tmp[t[l] - 96] == pre[b[i].r][t[l] - 96] - pre[b[i].l - 1][t[l] - 96]) {
					f[i][j] = l - j;
					flag = 1;
					break;
				}
				tmp[t[l] - 96]++;
			}
			if (!flag && j + b[i].len <= m)
				f[i][j] = b[i].len + f[i + 1][j + b[i].len];
			memset(tmp, 0, sizeof(tmp));
			flag = 0;
			for (int l = j - 1; l > j - b[i - 1].len && l >= 1; l--) {
				if (tmp[t[l] - 96] == pre[b[i - 1].r][t[l] - 96] - pre[b[i - 1].l - 1][t[l] - 96])
					break;
				tmp[t[l] - 96]++;
				flag++;
			}
			ans = std::max(f[i][j] + flag, ans);
		}
	printf("%d", ans);
}