【扫描线】luogu_P1502 窗口的星星

题意

有\(n\)个星星，第\(i\)个星星坐标为\((x_i,y_i)\)用一个宽为\(W\)，高为\(H\)的矩形去框住他们，矩形不能旋转只能平移，求出矩形中星星亮度之和的最大值（处于边框上的星星不算）。

数据范围：\(1≤T≤10，1\le n \le 10^4，1\le W,H \le 10^6，0\le x_i,y_i < 2^{31}\)

思路

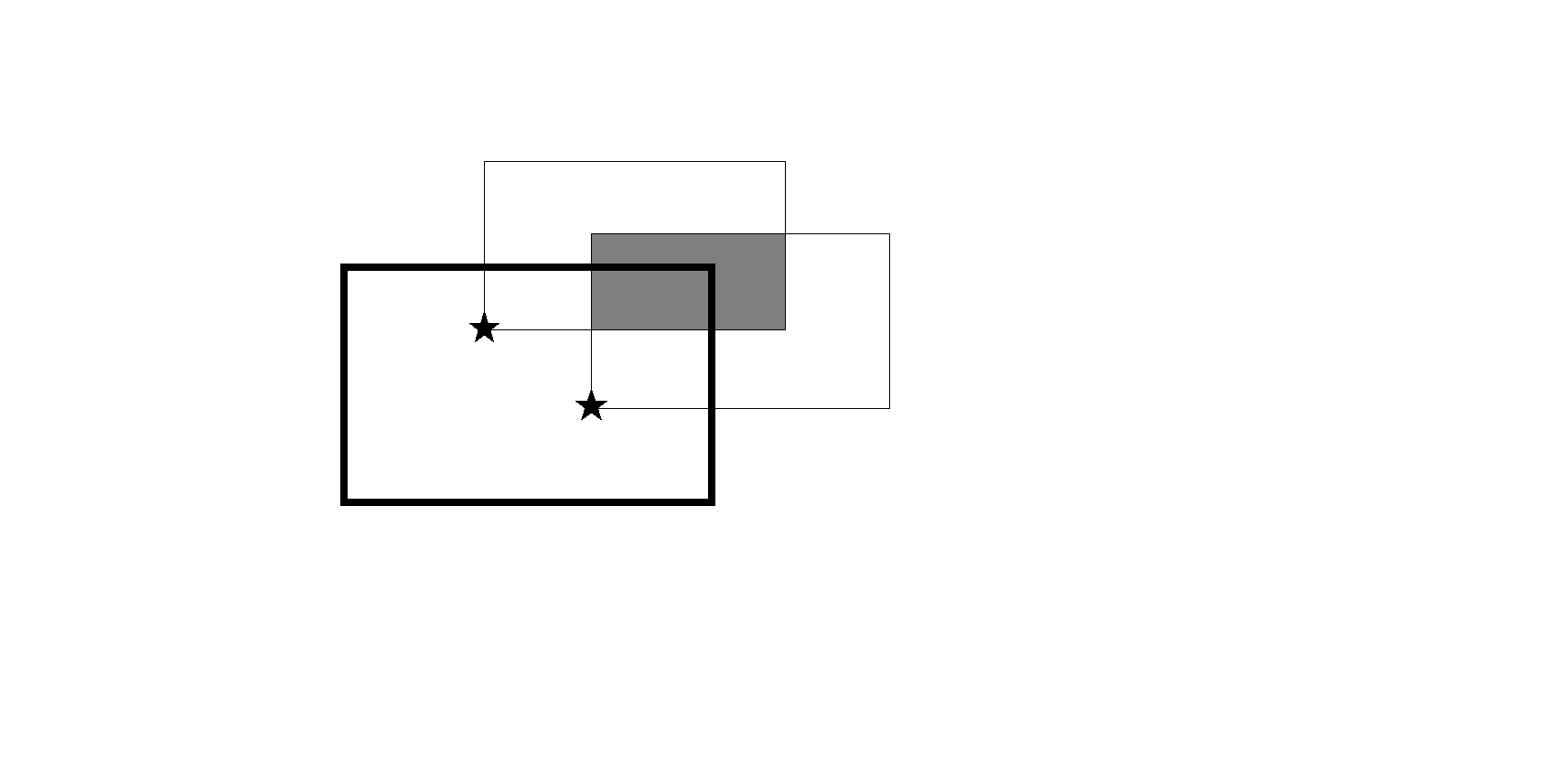
因为矩形大小限定了，所以可以由任意一个顶点来确定它，这里考虑矩形的右上角放在什么地方取得最大值。

（如图所示）对于一个星星，能圈住它的矩形的右上角的范围在\((x\sim x+w-1,y\sim y+h-1)\)，\(-1\)是因为边框不算。这个范围也就形成了一个矩形。
那么对于多个星星，如果能圈住它们的范围矩形有交集，那么代表它们可以被一个矩形同时框到。
对于每个星星的范围矩形，赋予它星星的亮度，那么多个星星的范围矩形的交集即为多个星星亮度之和。
答案即转化为要求一堆范围矩形中交集的最大值，这个我们可以用扫描线做。
具体的，把每个矩形转化为两条线，一条赋值\(l\)，一条赋值\(-l\)，在之前做过求矩形并，这里求得是交的最大值，那么线段树维护的是当前区间最大值和即可，要支持区间加减操作。

一些细节：多组数据答案要清空。
\(x,y\)的范围是\(int\)内的，矩形长宽的范围最大是\(1e6\)，加起来有可能爆\(int\)，要用\(longlong\)。
对于扫描线操作中，扫描的边按高度排序后，还要按赋值排序（大到小），因为同时覆盖了这条线，我们先要把覆盖到的也一起加上算最大值，再减去出去的矩形（即排序的目的是让正数在前面）。

代码

#include <cstdio>
#include <cstring>
#include <algorithm>
#define int long long

struct treenode {
	int l, r, res, add;
}tree[80001];
struct node{
	int l, r, h, mark;
}line[20001];
int t, n, w, h, tot, ans;
int X[20001];

bool cmp(node x, node y) {
	return x.h == y.h? x.mark > y.mark : x.h < y.h;
}

void build(int p, int l, int r) {
	tree[p].l = l;
	tree[p].r = r;
	tree[p].res = tree[p].add =  0;
	if (l == r) return;
	int mid = l + r >> 1;
	build(p << 1, l, mid);
	build(p << 1 | 1, mid + 1, r);
}

void spread(int p) {
	if (tree[p].add) {
		tree[p << 1].res += tree[p].add;
		tree[p << 1 | 1].res += tree[p].add;
		tree[p << 1].add += tree[p].add;
		tree[p << 1 | 1].add += tree[p].add;
		tree[p].add = 0;
	}
}

void change(int p, int L, int R, int val) {
	int l = X[tree[p].l], r = X[tree[p].r];
	if (r < L || l > R) return;
	if (l >= L && r <= R) {
		tree[p].add += val;
		tree[p].res += val;
		return;
	}
	spread(p);
	change(p << 1, L, R, val);
	change(p << 1 | 1, L, R, val);
	tree[p].res = std::max(tree[p << 1].res, tree[p << 1 | 1].res);
}

signed main() {
	scanf("%lld", &t);
	for (; t; t--) {
		memset(tree, 0, sizeof(tree));
		scanf("%lld %lld %lld", &n, &w, &h);
		for (int i = 1; i <= n; i++) {
			int x, y, l;
			scanf("%lld %lld %lld", &x, &y, &l);
			X[i * 2 - 1] = x;
			X[i * 2] = x + w - 1;
			line[i * 2 - 1] = (node){x, x + w - 1, y, l};
			line[i * 2] = (node){x, x + w - 1, y + h - 1, -l};
		}
		n <<= 1;
		std::sort(line + 1, line + n + 1, cmp);
		std::sort(X + 1, X + n + 1);
		int tot = std::unique(X + 1, X + n + 1) - (X + 1);
		build(1, 1, tot);
		ans = 0; 
		for (int i = 1; i <= n; i++) {
			change(1, line[i].l, line[i].r, line[i].mark);
			ans = std::max(ans, tree[1].res);
		}
		printf("%lld\n", ans);
	}
}