【状压DP】Y

题意

一个图中，每条边的边权是0或1，求出长度为d的不同的路径数（路径即经过边的01串）。

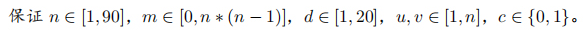
思路

考虑折半，最后把\(d\)分成2部分的01串组合起来。
设\(dp_i\)为状态为\(i\)时的终点点集，\(f_i\)为状态为\(i\)时的起点点集（2个bitset）。
枚举2段01串，判断是否存在中间点可以转移，累加答案。

代码

#include <cstdio>
#include <bitset>

const int MAXS = 1 << 11;
std::bitset<91> dp[MAXS], f[MAXS], g0[91], g1[91];
int n, m, d, d1, d2, ans;

int main() {
	scanf("%d %d %d", &n, &m, &d);
	for (int i = 1, u, v, c; i <= m; i++) {
		scanf("%d %d %d", &u, &v, &c);
		c ? g1[u][v] = g1[v][u] = 1 : g0[u][v] = g0[v][u] = 1;
	}
	d2 = d >> 1;
	d1 = d - d2;//钦定d1>=d2，dp处理d2的部分，f处理d1的部分
	for (int u = n; u; u--) {
		for (int i = 0; i < MAXS; i++)
			dp[i].reset();
		dp[1][u] = 1;//在前面放1钦定状态的长度，起点为u
		for (int i = 1; i < 1 << d1; i++)
			for (int j = 1; j <= n; j++)
				if (dp[i][j]) {
					dp[i << 1] |= g0[j];
					dp[i << 1 | 1] |= g1[j];//左移即下一位是0，|1即下一位为1
				}
		for (int i = 0; i < 1 << d1; i++)
			f[i][u] = dp[1 << d1 | i].any();//u为起点，状态为i
	}
	for (int i = 0; i < 1 << d1; i++)
		for (int j = 0; j < 1 << d2; j++)
			if ((dp[1 << d2 | j] & f[i]).any()) ans++;//有中转点
	printf("%d", ans);
}