【数学 并查集】X

题意

给出\(n\)个数，将它们划分成2个集合，求出\(gcd\)(第1个集合的乘积，第2个集合的乘积）=1的划分方案有多少种。

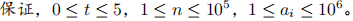
思路

如果\(2\)个数的\(gcd\neq 1\)那么它们就必须同属\(1\)个集合。
对于每个数的质因子，将它们放在一个联通块中，代表含有这些质因子的数都要属于同一个集合。
如果数字可以放在任意一个集合，答案为\(2^n-2\)，所以\(gcd=1\)答案为\(2^{联通块的个数}-2\)

代码

#include <cstdio>
#include <algorithm>

const int MOD = 1e9 + 7;
int t, n, cnt;
int prime[1000001], v[1000001], oo[1000001], fa[1000001];

int find(int x) {
	return fa[x] = fa[x] == x ? x : find(fa[x]);
}

int power(int a, int b) {
	int res = 1;
	for (; b; b >>= 1) {
		if (b & 1) res = (long long)res * a % MOD;
		a = (long long)a * a % MOD;
	}
	return res;
}

int main() {
	scanf("%d", &t);
	for (int i = 2; i <= 1000000; i++) {
		if (!v[i]) {
			v[i] = i;
			prime[++cnt] = i;
		}
		for (int j = 1; j <= cnt; j++) {
			if (prime[j] > v[i] || prime[j] > 1000000 / i) break;
			v[i * prime[j]] = prime[j];
		}
	}
	for (int a; t; t--) {
		int tot = 0;
		scanf("%d", &n);
		for (int i = 1; i <= 1000000; i++)
			fa[i] = i;
		oo[0] = 0;
		for (int i = 1; i <= n; i++) {
			scanf("%d", &a);
			if (a == 1) tot++;
			int last = 0;
			while (a >= 2) {
				int xx = v[a];
				while (a % xx == 0) a /= xx;
				oo[++oo[0]] = xx;
				if (last) {
					int f1 = find(last), f2 = find(xx);
					fa[f2] = f1;
				}
				last = xx;
			}
		}
		std::sort(oo + 1, oo + oo[0] + 1);
		int m = std::unique(oo + 1, oo + oo[0] + 1) - (oo + 1);
		for (int i = 1; i <= m; i++)
			if (fa[oo[i]] == oo[i]) tot++;
		printf("%d\n", power(2, tot) - 2);
	}
}