【线段树 扫描线】luogu_P5490 【模板】扫描线

题意

给出\(n\)个矩形。
一个矩形的左下角坐标为\((x_1,y_1)\)，右上角坐标为\((x_2,y_2)\)。

数据范围：\(1 \le n \le 10^5, 0 \le x_1 < x_2 \le 10^9, 0 \le y_1 < y_2 \le 10^9\)。

思路

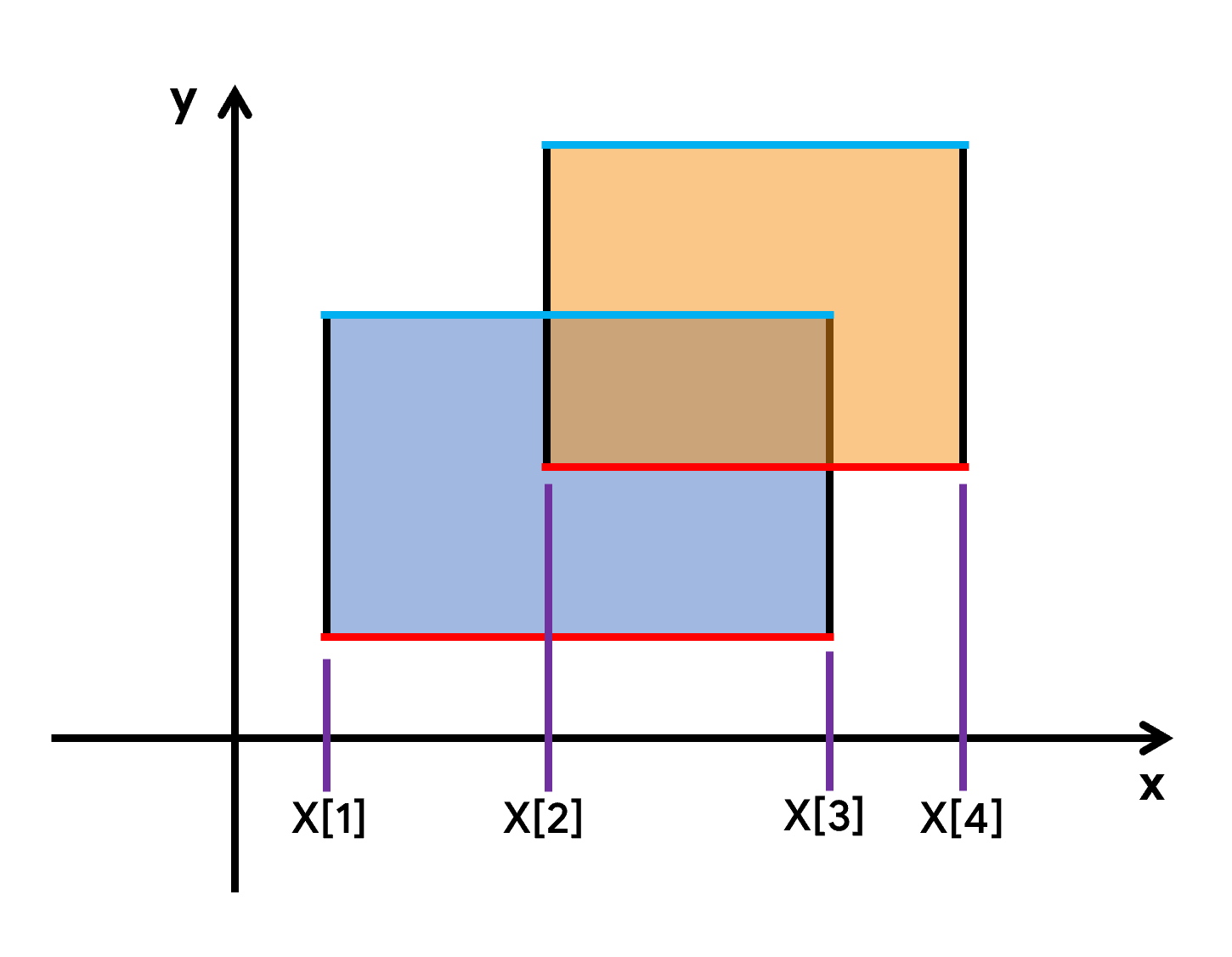
设想一条平行于\(x\)轴的扫描线从下往上扫过整个图形，根据矩形的面积求法，扫过面积等于当前扫到的区间长度\(*\)当前扫过的高度。
用线段树维护当前扫到的区间长度即可。

具体实现：每个矩形分成\(2\)条边，一条赋值\(1\)，一条赋值\(-1\)，\(1\)代表扫到这个矩形时对区间长度做出的贡献，\(-1\)代表扫完后退出。每次都用(下一条边的\(y\)坐标-当前边的\(y\)坐标）\(*\)当前区间长度来累加答案。
坐标较大，都要离散。

有些细节：因为给的点坐标，线段树\([l,r]\)记录的是点\(l\sim\)点\(r+1\)之间的区间。

时间复杂度较多在线段树操作上，即为\(O(nlog_2n)\)

代码

#include <cstdio>
#include <algorithm>

int n;
long long ans;
int x1, y1, x2, y2;
int X[2000001];

struct treenode {//扫描线信息
	int l, r, len, sum;//离散后点的l，r，矩形覆盖长度，被几个矩形覆盖
}tree[4000001];
struct node {
	int l, r, h, mark; 
}line[2000001];

int cmp(node x, node y) {
	return x.h < y.h;
}

void build(int p, int l, int r) {
	tree[p].l = l;
	tree[p].r = r;
	tree[p].len = tree[p].sum = 0;
	if (l == r) return;
	int mid = l + r >> 1;
	build(p << 1, l, mid);
	build(p << 1 | 1, mid + 1, r);
}

void spread(int p) {
	int l = X[tree[p].l], r = X[tree[p].r + 1];
	if (tree[p].sum) tree[p].len = r - l;
	else tree[p].len = tree[p << 1].len + tree[p << 1 | 1].len;
}

void change(int p, int L, int R, int val) {
	int l = X[tree[p].l], r = X[tree[p].r + 1];
	if (r <= L || l >= R) return;
	if (l >= L && r <= R) {
		tree[p].sum += val;
		spread(p);
		return;
	}
	change(p << 1, L, R, val);
	change(p << 1 | 1, L, R, val);
	spread(p);
}

int main() {
	scanf("%d", &n);
	for (int i = 1; i <= n; i++) {
		scanf("%d %d %d %d", &x1, &y1, &x2, &y2);
		X[2 * i - 1] = x1;
		X[2 * i] = x2;
		line[2 * i - 1] = (node){x1, x2, y1, 1};
		line[2 * i] = (node){x1, x2, y2, -1};//添加边
	}
	n <<= 1;
	std::sort(line + 1, line + n + 1, cmp);
	std::sort(X + 1, X + n + 1);
	int tot = std::unique(X + 1, X + n + 1) - (X + 1);
	build(1, 1, tot - 1);//[X_1~X_tot]的区间，即总区间
	for (int i = 1; i < n; i++) {
		change(1, line[i].l, line[i].r, line[i].mark);
		ans += (long long)tree[1].len * (line[i + 1].h - line[i].h);
	}
	printf("%lld", ans);
}