模拟赛题解

T1 辣椒树

题面描述

给定一颗树，求分成三部分后的最小差异值。

• 子任务一，$20$分，保证 $N ≤ 200$；
• 子任务二，$30$分，保证 $N ≤ 2000$；
• 子任务三，$50$分，$N ≤ 2 × 10^5$。

题解

暴力：每次枚举两个点，将其父边断掉，如果存在祖先关系则特判一下，复杂度 $O(n^2)$ ，预计 $50pts$

正解： $dfs$ 搜索每个结点，砍掉它的父边，剩下的尽量等分（易证）。

这一步可以用 $multiset$ 维护。

对于一个点，将其到根节点的链上的点放入 $s2$ ，再将这条链左边的所有点放入$s1$

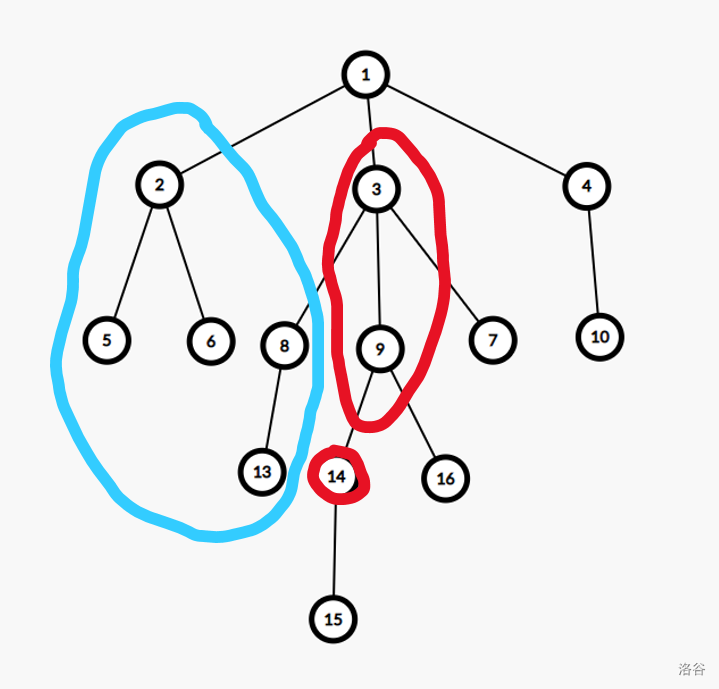
然后令 $x= \dfrac{n-siz[u]}{2}$。 在 $s1$ 中查找最靠近 $x$ 的两个数，在 $s2$ 中查找最靠近 $x+siz[u]$ 的两个数，四种情况讨论一下。

细节：$dfs$ 到一个点时将其放入 $s1$，回溯的时候将其从 $s1$ 中删除，并插入到 $s2$ 中。

预计 $100pts$ 。

code

T2 括号序列

题面描述

给你一个由小写字母组成的字符串 $s$，要你构造一个字典序最小的合法的括号序列与这个字符串匹配。

字符串和括号序列匹配定义为：首先长度必须相等，其次对于一对匹配的左括号和右括号 $i,j$，必须有 $s_i=s_j$。

无解输出 -1。

对于 10% 的数据，保证 $2 ≤ |S| ≤ 20$。

对于 50% 的数据，保证 $2 ≤ |S| ≤ 7000$。

对于 100% 的数据，保证 $2 ≤ |S| ≤ 10^5$。

题解

暴力1：直接 $dfs$ 枚举每个位置状态，复杂度 $O(2^n)$ ，预计 $10pts$ 。

暴力2：考虑贪心，如果一个左括号有多个合法的右括号匹配，则一定选最靠右的，而一对括号匹配当且仅当字符相同且中间部分可以完全匹配。

怎么判断能否一段连续区间可以完全匹配呢？我们可以用栈模拟！

假设该区间为 $[l, r]$ 。如果栈在 $l-1$ 时的形态与 $r$ 时的形态相同，则可以匹配。

而栈的形态我们可以用字符串哈希记录。

所以我们只需要 $O(n)$ 预处理出每个位置的哈希值，然后对于每一个点，从右往左找第一个哈希值相等的位置，递归处理即可。复杂度 $O(n^2)$ ，预计 $50pts$ 。

正解：现在的瓶颈是如何 $O(1)$ 找到最靠右的匹配位置。

我们可以每个点的哈希值离散化并存入 $vector$ 中进行分类。

然后对于当前状态 $dfs(l, r)$ ，我们二分坐标在 $[l, r]$ 范围中与 $l$ 匹配且最靠右的位置，即在 $vec[hash[l]]$ 中进行 upper_bound。

最后复杂度均摊下来就是 $O(nlogn)$ ，预计 $100pts$ 。

code

T3 路由表

题面

link

题解

暴力1：按照题意模拟即可，复杂度 $O(32n^2)$ ，预计 $30pts$ 。

暴力2：将 $IP$ 地址用 unsigned int 存下来，比较 $a$，$b$ 是否匹配就只需要判断 $(a>>len)==(b>>len)$ 即可，复杂度 $O(n^2)$，预计 $50pts$ 。

正解：考虑将当前插入的所有 $IP$ 地址建成一颗 $01Trie$ ，结尾打上标记。

对于每次询问，将路径上的所有标记存入一个维护单调递增序列的栈，二分 $l$ 和 $r$ 的位置并计算一下差值就行了。（信息量有些大......）

复杂度线性，预计 $100pts$ 。

code

T4 旅游路线

题面

link

题解

此处只讲正解。

因为钱花得越多，走的路程也就越多，所以可以二分钱数，然后判断最远路程是否符合预期。

定义 $f[i][j]$ 表示从 $i$ 出发，初始油空，用了不超过 $j$ 的钱，最多能跑多远。

$f[i][j]=max(f[k][j-c[i]]+w[i][k])$

其中 $w[i][j]$ 表示从 $i$ 走到 $j$ ，初始油满（假设为 $C$ ），最多能跑多远。

计算 $w[i][j]$ 采用倍增。

预处理 $dis[k][i][j]$ 表示用了 $2^k$ 的油，从 $i$ 到 $j$ 最多能跑多远。

$dis[k][i][j]=max(dis[k-1][i][mid]+dis[k-1][mid][j])$

辅助地，定义 $g[k][i][j]$ 表示依次考虑了 $2^0$ ，$2^1$ ，$2^2$ ，......，$2^k$ 的油耗，从 $i$ 到 $j$ 最多能跑多远。

若 $C$ 二进制下第 $k$ 位是 $0$ ，那么 $g[k][i][j]=g[k-1][i][j]$ 。

若 $C$ 二进制下第 $k$ 为是 $1$ ，那么 $g[k][i][j] = max(g[k - 1][i][mid] + dis[k][mid][j] )$ 。

最后 $w[i][j]=g[k_{max}][i][j]$ 。

$DP$ 采取记忆化搜索。

复杂度 $O(n^3logC)$ ，预计 $100pts$ 。

code