openmp #pragma omp task优化

0.注意事项

本文所有测试均为x86处理器，所有测试代码的位置为：https://github.com/Beichen-Wang/HPCTest/tree/master/OpenMPTest

 

1.基本原理

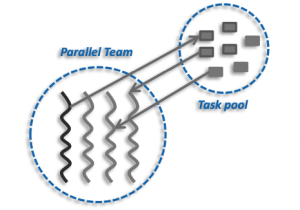
#pragma omp task的基本原理如下图所示，一个是线程池，一个是任务池，每个线程执行任务池中的一个任务。

 

2.使用方法

具体查看README，要注意添加-fopenmp；

3.关键命令

task支持做两种操作：

• 一种是recursive function，按照查到的官方教程中的经典例子，最经典的计算斐波那契数列；

•  另外一种是unbounded loops：

 

3.1 计算斐波那契数列

int OmpFib(int n) {
  int x, y;
  if (n < 2) {
    return n;
  }
#pragma omp task shared(x)
  { x = OmpFib(n - 1); }
#pragma omp task shared(y)
  { y = OmpFib(n - 2); }
#pragma omp taskwait
  return x + y;
}

#pragma omp parallel num_threads(2)
  {
#pragma omp single
    { OmpFib(Num); }
  }

此外还有一个普通的斐波那契数列作为参照：

int NorFib(int n) {
  int x, y;
  if (n < 2)
    return n;
  x = NorFib(n - 1);
  y = NorFib(n - 2);
  return x + y;
}

测试时间结果为：

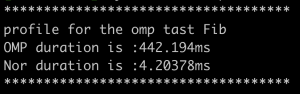
这里发生了非常严重的负优化，猜测原因为task被切分的太细，每个task执行的任务非常短；所以我在这里做了cutoff：

int OmpFib(int n) {
  int x, y;
  if (n < 2) {
    return n;
  }
  if(n > 20){
#pragma omp task shared(x) untied
  { x = OmpFib(n - 1); }
#pragma omp task shared(y) untied
  { y = OmpFib(n - 2); }
#pragma omp taskwait
  } else {
    x = OmpFib(n - 1);
    y = OmpFib(n - 2);
  }
  return x + y;
}

双线程的效果良好，测试结果为：

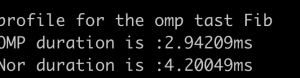
3.2unbounded loops

OMP task的版本：

        int OMPProcess(){
            mulSum = 1;
            NodeList * current;
            current = node.get();
            #pragma omp parallel num_threads(2)
            {
                #pragma omp single 
                {
                    while(current){
                        #pragma omp task
                            subProcess.template operator()<decltype(&SubProcess::SubProcess1)>(mulSum, current->val);
                        current = (current->next).get();
                    }
            }
            }
            return mulSum;
        }
    

Normal版本：

int NorProcess(){
           mulSum = 1;
            NodeList * current;
            current = node.get();
            while(current){
                subProcess.template operator()<decltype(&SubProcess::SubProcess1)>(mulSum, current->val);
                current = (current->next).get();
            }
            return mulSum;
        }

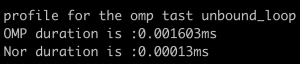
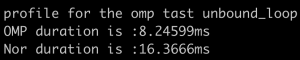
• SubProcess1

  • 

• SubProcess2

  • 

3.3 #pragma omp taskloop

其基本语法为：

#pragma omp taskloop [clause[, clause] ...]
for (init-expr; test-expr; incr-expr)
{
    // loop body
}

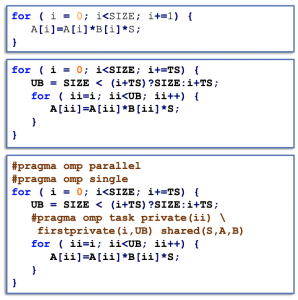
下面来用task和用taskloop来分别对一个循环做处理：

• task的实现方式：

  

• taskloop的实现方式：

可以看到taskloop的实现方式更简单，其中grainsize就是tilesize，我也做了测试，测试核心代码为：

class GrainSizeSubProcess final: public SubProcessBase {
public:
  size_t operator()(size_t n) override {
    size_t sum = 0;
#pragma omp taskloop grainsize(100000) shared(sum)
    for (size_t i = 0; i < n - 1; i++) {
      sum += (i * (i + 1));
    }
    return sum;
  }
};

• 此处grainsize我选用的是100000，n为500000时，测试结果为：

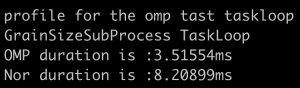
• 同样，当grainsize过小时，同样会造成负优化，所以每一个task所处理的grain size不应该过小；

4.总结

• 如果产生task的数量过多且每个task处理的内容很少，会发生极其严重的负向优化；
• 在unbloundloop结构中，如果process的的内容与前后的task有关(reduce除外)，也是负向优化；
• 在unbloundloop结构中，只有每个task处理的内容与前后无关，会产生正向优化；
• taskloop可以有效降低运行时间，但是grainsize不应该选用过小；