5.26~6.1
基环树
基环树不是树,而是只有一个连通环的图,它有$ n \(个点和\) n $条边。
- 无向图上的基环树。在一颗基于无向图的无根树加上一条边,就形成了基环树。去掉环上任意一条边,基环树就变成了一颗真正的树
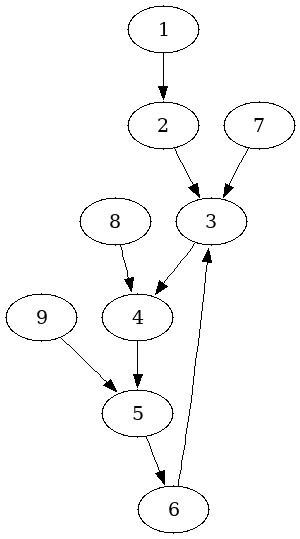
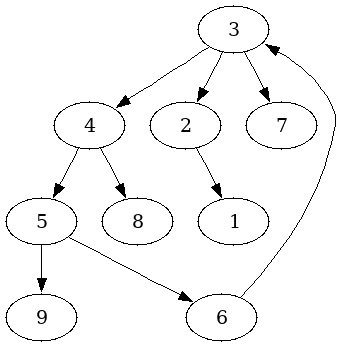
- 有向图上的基环树。一个有向无环图,如果能在图中加一条边形成一个自连通的环,则形成一颗基环树。把环看成一个整体,根据它与环外点的关系,把基环树分为两种:内向树,环外的点只能进入环内,所有边都指向环;外向树,环外的点无法进入环内,所有边都背离环。
(图是丑了一点,意思到位就行...)
基环树的找环问题,就是“图的连通性”的一个简化问题。
无向图,用拓扑排序的BFS找出环,操作结束后,度数大于$ 1 \(的点就是环上的点。具体做法:①计算所有点的度数;②把所有度数为\) 1
\(的点入队;③队列弹出度数为1的点,把它连的所有边都去掉,并将边所连的邻居点的度数减\) 1
\(,如果这个邻居的度数变为\) 1
\(就入队;④重复以上操作,直到队列为空。操作结束后,统计度数大于\) 1
$的点,就是环上的点。(这种找环的方法只适用于只有一个环的基环树)
找环上的一点,用DFS可以方便的找到:如果一个点$ v \(第二次被访问,那么就存在环,且\) v $在环上。这个方法同时适用于有向图和无向图。
看一道例题:洛谷P2607

树形DP+基环树
骑士之间的关系构成了基环树森林。并且这道题从任意一个节点出发,一定可以找到一个环。所以解体主要是找到一个环,并用mark记录环上一点,把这个点的一条边断开,然后分别在父节点和子节点上做树上DP,取最大值;再去找其它没有访问过的环重复操作。
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
const int maxn = 1e6+5;
class node{
public:
int father,val;
}p[maxn];
vector <int> G[maxn];
int n,mark;
bool vis[maxn];
ll dp[maxn][2];
void add(int i,int f,int v){
G[f].push_back(i);
p[i] = {f,v};
}
int findp(int u){
vis[u] = 1;
int f = p[u].father;
if(vis[f]) return f;
else return findp(f);
}
void dfs(int u){
dp[u][0] = 0;
dp[u][1] = p[u].val;
vis[u] = 1;
for(auto v:G[u]){
if(v == mark) continue;
dfs(v);
dp[u][1] += dp[v][0];
dp[u][0] += max(dp[v][0],dp[v][1]);
}
}
ll solve(int u){
ll res = 0;
mark = findp(u);
dfs(mark);
res = max(res,dp[mark][0]);
mark = p[mark].father;
dfs(mark);
res = max(res,dp[mark][0]);
return res;
}
int main(void){
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
cin >> n;
for(int i=1;i<=n;i++){
int v,f;
cin >> v >> f;
add(i,f,v);
}
ll ans = 0;
for(int i=1;i<=n;i++){
if(!vis[i]) ans += solve(i);
}
cout << ans << '\n';
return 0;
}
洛谷P1453 城市环路

基环树+树形DP
基环树用拓扑排序来找到环上一条边,也就是两个点,然后断开这条边,分别以两个点为根进行树上DP,求出最大值
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e5+5;
using pii = pair<int,int>;
int n,ans = 0,dp[maxn][2],in[maxn],val[maxn];
vector <int> e[maxn];
queue <int> q;
double k;
bool vis[maxn];
pii topo(){
for(int i=1;i<=n;i++)
if(in[i] == 1) q.push(i);
while(!q.empty()){
int t = q.front();
q.pop();
in[t]--;
for(auto i:e[t]){
in[i]--;
if(in[i] == 1) q.push(i);
}
}
int index;
for(int i=1;i<=n;i++)
if(in[i] > 1) index = i;
for(auto i:e[index])
if(in[i] > 1) return {index,i};
}
void dfs(int x){
dp[x][0] = 0;
dp[x][1] = val[x];
vis[x] = 1;
for(auto i:e[x]){
if(vis[i]) continue;
dfs(i);
dp[x][1] += dp[i][0];
dp[x][0] += max(dp[i][1],dp[i][0]);
}
}
void solve(){
pii mark = topo();
dfs(mark.first);
ans = max(ans,dp[mark.first][0]);
memset(vis,0,sizeof(vis));
dfs(mark.second);
ans = max(ans,dp[mark.second][0]);
}
int main(void){
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
cin >> n;
for(int i=1;i<=n;i++) cin >> val[i];
for(int i=1;i<=n;i++){
int u,v; cin >> u >> v;
in[++u]++,in[++v]++;
e[u].push_back(v);
e[v].push_back(u);
}
cin >> k;
solve();
cout << fixed << setprecision(1) << k*ans << '\n';
return 0;
}
🏀杯第14届国赛
这里可以找到第14届C++国赛的题
填空A
dp
先把1到2023的序列转换为字符串,再dp转移
要转移四次,分别对应“2023”里的四位数字
状态转移方程:
$ 若s[i] == 当前数字,dp[i] = dp[i-1] + dp_{pre}[i-1] $
$ 否则,dp[i] = dp[i-1] $
$ dp_{pre}表示2023里某位数字的前一个数字的dp $
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
const int maxn = 7000;
ll f21[maxn],f0[maxn],f22[maxn],f3[maxn];
int main(void){
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
string s;
stack <int> z;
for(int i=1;i<=2023;i++){
int j = i;
if(j >= 10){
while(j >= 10){
z.push(j % 10);
j /= 10;
}
s = s + char('0' + j);
while(!z.empty()){
char c = '0' + z.top();
z.pop();
s = s + c;
}
}
else s = s + char('0' + j);
}
int si = s.size();
s = ' ' + s;
for(int i=1;i<=si;i++){
f21[i] = f21[i-1] + (s[i] == '2');
}
for(int i=1;i<=si;i++){
f0[i] = (s[i] == '0' ? f0[i-1] + f21[i-1] : f0[i-1]);
}
for(int i=1;i<=si;i++){
f22[i] = (s[i] == '2' ? f22[i-1] + f0[i-1] : f22[i-1]);
}
for(int i=1;i<=si;i++){
f3[i] = (s[i] == '3' ? f3[i-1] + f22[i-1] : f3[i-1]);
}
cout << f3[si];
return 0;
}
填空B
埃氏筛+枚举+剪枝
剪枝有坑!普通剪枝会有爆long long的问题,算出来的答案比正确答案多10
应该用除法判断来避免爆ll
if(prime2[i] > sup/prime2[j]) break;
#include <bits/stdc++.h>
#define int long long
using namespace std;
const int maxn = 1e7+10;
const int inf = 2333, sup = 23333333333333;
bool vis[maxn];
vector <int> prime,prime2;
void ps(){
for(int i=2;i*i<=maxn;i++){
if(!vis[i])
for(int j=i*i;j<=maxn;j+=i)
vis[j] = 1;
}
for(int i=2;i<=maxn;i++)
if(!vis[i]) prime.push_back(i);
for(auto i:prime)
if(i*i <= sup) prime2.push_back(i*i);
}
int solve(){
ps();
int cnt = 0, si = prime2.size();
for(int i=0;i<si;i++){
for(int j=i+1;j<si;j++){
if(prime2[i] > sup/prime2[j]) break;
int num = prime2[i] * prime2[j];
if(num >= inf && num <= sup) cnt++;
}
}
return cnt;
}
signed main(void){
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
cout << solve() << '\n';
return 0;
}
C
简单的模拟,分类讨论。
计算缺和多的个数,并分类讨论即可
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e5+5;
map <int,int> ma;
int main(void){
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
int n; cin >> n;
for(int i=1;i<=n;i++){
int c; cin >> c;
ma[c]++;
}
int que = 0, duo = 0;
for(auto i:ma){
if(i.second == 1) que++;
else if(i.second > 2) duo += i.second - 2;
}
int ans = min(que,duo), res = max(que,duo) - ans;
//cout << que << ' ' << duo << '\n';
if(que < duo) ans += res;
else ans += res/2;
cout << ans << '\n';
return 0;
}
D
双指针
由题目的意思可以知道,两个数组一定是可以通过合并相邻元素而全等的,因此可以双指针,一个指q1,一个指q2,从头开始走。如果碰到p1不等于p2,就进行合并,知道相等为止
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e5+10;
int n,m,cnt = 0;
vector <int> q1,q2;
void solve(){
vector<int>::iterator it1,it2;
it1 = q1.begin(), it2 = q2.begin();
while(it1 != q1.end() && it2 != q2.end()){
if(*it1 == *it2) it1++,it2++;
else if(*it1 < *it2){
int temp = *it1;
while(temp != *it2){
it1++, cnt++;
temp += *it1;
}
it1++,it2++;
}
else{
int temp = *it2;
while(temp != *it1){
it2++, cnt++;
temp += *it2;
}
it1++,it2++;
}
}
cout << cnt << '\n';
}
int main(void){
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
cin >> n >> m;
for(int i=1;i<=n;i++){
int a; cin >> a;
q1.push_back(a);
}
for(int i=1;i<=m;i++){
int b; cin >> b;
q2.push_back(b);
}
solve();
return 0;
}
E
走迷宫plus版
vis数组的第三个维度是个巧思,能使bfs正确判重
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e3+5;
int n,m,k;
char room[maxn][maxn];
bool vis[maxn][maxn][11];
int explore[][2] = {0,1,0,-1,1,0,-1,0};
class node{
public:
int x,y,st,s;
};
inline bool check(node p){
return p.x>=1 && p.x<=n && p.y>=1 && p.y<=m;
}
void bfs(){
queue <node> q;
q.push({1,1,0,1});
while(!q.empty()){
node start = q.front();
q.pop();
if(start.x == n && start.y == m){
cout << start.st<< '\n';
return;
}
if(vis[start.x][start.y][start.s]) continue;
vis[start.x][start.y][start.s] = 1;
if(start.s == k){
for(int i=0;i<4;i++){
node next = {start.x+explore[i][0],start.y+explore[i][1],start.st+1,1};
if(check(next) && room[start.x][start.y] != room[next.x][next.y])
q.push(next);
}
}
else{
for(int i=0;i<4;i++){
node next = {start.x+explore[i][0],start.y+explore[i][1],start.st+1,start.s+1};
if(check(next) && room[start.x][start.y] == room[next.x][next.y])
q.push(next);
}
}
}
cout << "-1\n";
return;
}
int main(void){
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
cin >> n >> m >> k;
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
cin >> room[i][j];
bfs();
return 0;
}
复习高代去了,端午一结束就考试 T_T


 浙公网安备 33010602011771号
浙公网安备 33010602011771号