4.7~4.13
本部蓝桥试炼
续上回
B

线段树板子,但奈何我现在没法手撕线段树哇(码太长了)
遂选择树状数组,但是--按理说树状数组(nlog2n)的复杂度是能过此题的,而且赛后题解里也说了树状数组能过,为什么才拿25分??
(后来发现问题了--忘记取模,唉)
题补就写线段树的吧
#include <bits/stdc++.h>
#define int long long
using namespace std;
const int N = 1e5+10;
const int mod = 1e9+7;
int a[N];
int tree[N<<2];
int tag[N<<2];
int ls(int p){return p<<1;}
int rs(int p){return p<<1|1;}
void push_up(int p){
tree[p] = tree[ls(p)] + tree[rs(p)];
//tree[p] = min(tree[ls(p)],tree[rs(p)]);
}
void build(int p,int pl, int pr){
tag[p] = 0;
if(pl == pr){tree[p] = a[pl];return;}
int mid = (pl + pr) >> 1;
build(ls(p),pl,mid);
build(rs(p),mid+1,pr);
push_up(p);
}
void addtag(int p,int pl,int pr,int d){
tag[p] += d;
tree[p] += d*(pr-pl+1);
}
void push_down(int p,int pl,int pr){
if(tag[p]){
int mid = (pl+pr)>>1;
addtag(ls(p),pl,mid,tag[p]);
addtag(rs(p),mid+1,pr,tag[p]);
tag[p] = 0;
}
}
void update(int L,int R,int p, int pl,int pr,int d){
if(L<=pl && pr<=R){
addtag(p,pl,pr,d);
return;
}
push_down(p,pl,pr);
int mid = (pl+pr)>>1;
if(L <= mid) update(L,R,ls(p),pl,mid,d);
if(R > mid) update(L,R,rs(p),mid+1,pr,d);
push_up(p);
}
int query(int L,int R,int p,int pl,int pr){
if(pl >= L&&R >= pr) return tree[p];
push_down(p,pl,pr);
int res = 0;
int mid = (pl+pr)>>1;
if(L<=mid) res+=query(L,R,ls(p),pl,mid);
if(R>mid) res+=query(L,R,rs(p),mid+1,pr);
return res;
}
signed main(void){
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
int n,m;
cin >> n >> m;
for(int i=1;i<=n;i++)
cin >> a[i];
build(1,1,n);
while(m--){
int q,L,R,d;
cin >> q;
if(q == 1){
cin >> L >> R >> d;
update(L,R,1,1,n,d);
}
else{
cin >> L >> R;
cout << query(L,R,1,1,n)%mod << '\n';
}
}
return 0;
}
C
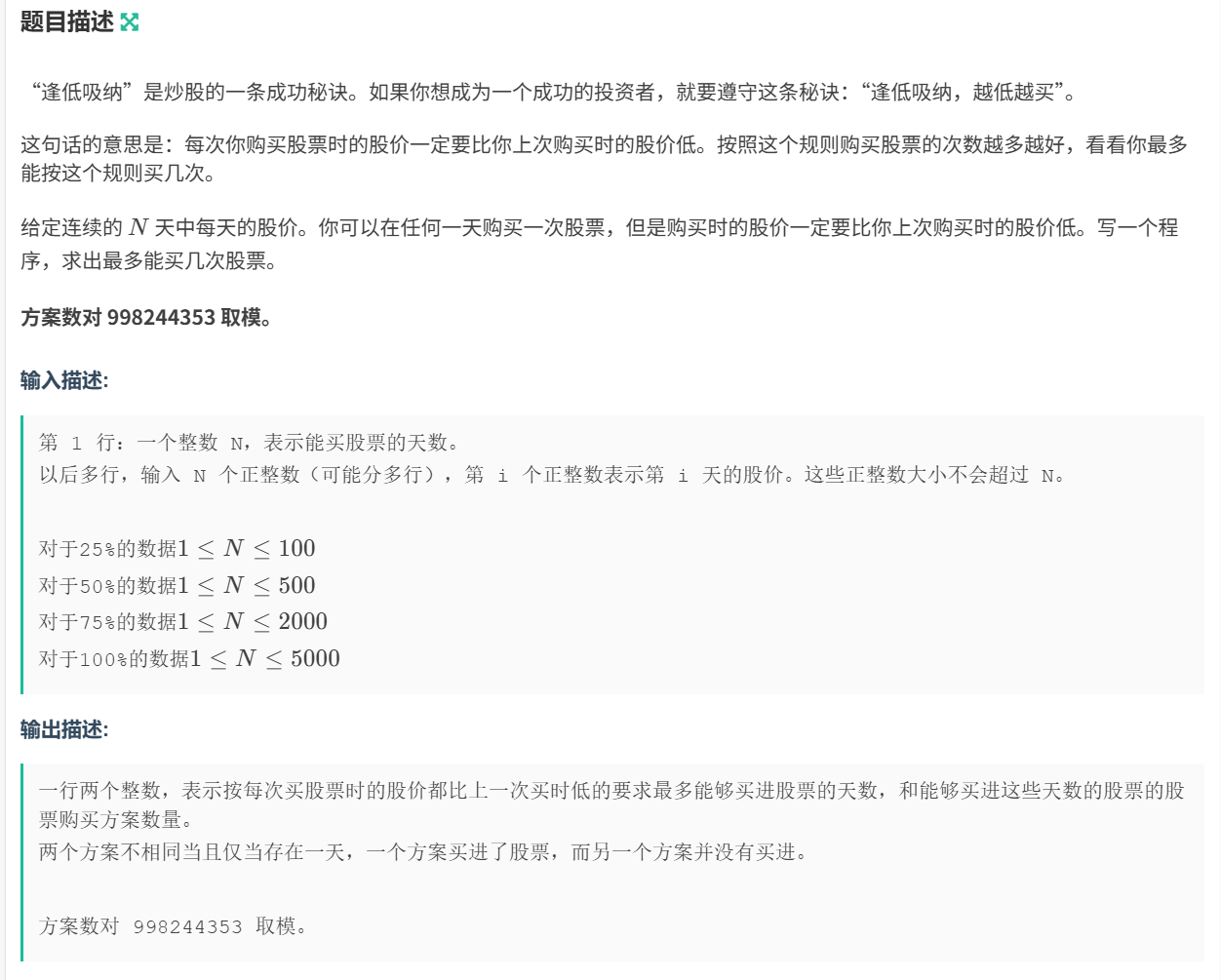
最长下降子序列,这题还加了一个方案数,会比基础dp麻烦一些,和B题一样,也要注意取模
code:
#include <bits/stdc++.h>
#define int long long
using namespace std;
const int maxn = 5005;
const int mod = 998244353;
int a[maxn],dp[maxn],way[maxn];
signed main(void){
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
int n;
cin >> n;
for(int i=1;i<=n;i++){
cin >> a[i];
dp[i] = 1;
way[i] = 1;
}
for(int i=2;i<=n;i++){
for(int j=1;j<i;j++){
if(a[j] > a[i]){
if(dp[i] == dp[j]+1)
(way[i]+=way[j])%=mod;
else if(dp[j]+1>dp[i]){
way[i] = way[j];
dp[i] = dp[j]+1;
}
}
}
}
int ans=1,ways=0;
for(int i=1;i<=n;i++)
if(dp[i] > ans) ans = dp[i];
for(int i=1;i<=n;i++)
if(dp[i] == ans) (ways+=way[i])%=mod;
cout << ans << ' ' << ways << '\n';
return 0;
}
A

填空题
用DFS暴力搜,剪枝啥的都不要,反正是填空题
#include <bits/stdc++.h>
using namespace std;
int ans = 0;
int a[6][6];
bool win(int x,int y,int k){
bool pd;
for(int i=1;i<=5;i++){
pd = 1;
for(int j=1;j<=5;j++){
if(a[i][j]!=k || (i==x&&j==y)){
pd = 0;
break;
}
}
if(pd) return 1;
pd = 1;
for(int j=1;j<=5;j++){
if(a[j][i]!=k || (j==x&&i==y)){
pd = 0;
break;
}
}
if(pd) return 1;
}
pd = 1;
for(int i=1;i<=5;i++){
if(a[i][i]!=k || (i==x&&i==y)){
pd = 0;
break;
}
}
if(pd) return 1;
pd = 1;
for(int i=1;i<=5;i++){
if(a[i][6-i]!=k || (i==x&&(6-i)==y)){
pd = 0;
break;
}
}
if(pd) return 1;
return 0;
}
bool check(){
int sum = 0;
for(int i=1;i<=5;i++)
for(int j=1;j<=5;j++)
if(a[i][j]) sum+=1;
if(sum!=13) return 0;
for(int i=1;i<=5;i++){
for(int j=1;j<=5;j++){
if(!a[i][j]) continue;
if(win(i,j,0) || win(i,j,1))
return 0;
}
}
return 1;
}
void dfs(int x,int y){
if(y == 6){
x++,y=1;
}
if(x == 6){
ans += check();
return;
}
a[x][y] = 1;
dfs(x,y+1);
a[x][y] = 0;
dfs(x,y+1);
}
int main(void){
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
dfs(1,1);
cout << ans << '\n';
return 0;
}
第15届蓝桥真题
填空AB

模拟人握手,第一个人握49次,第二个人握48次....倒数第二个人握1次,最后一个人没得握,这些次数求和,减去7个人之间握的次数即可
#include <bits/stdc++.h>
using namespace std;
int main(void){
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
int ans = 0;
for(int i=49;i>0;i--)
ans += i;
cout << ans-21 << '\n';
return 0;
}
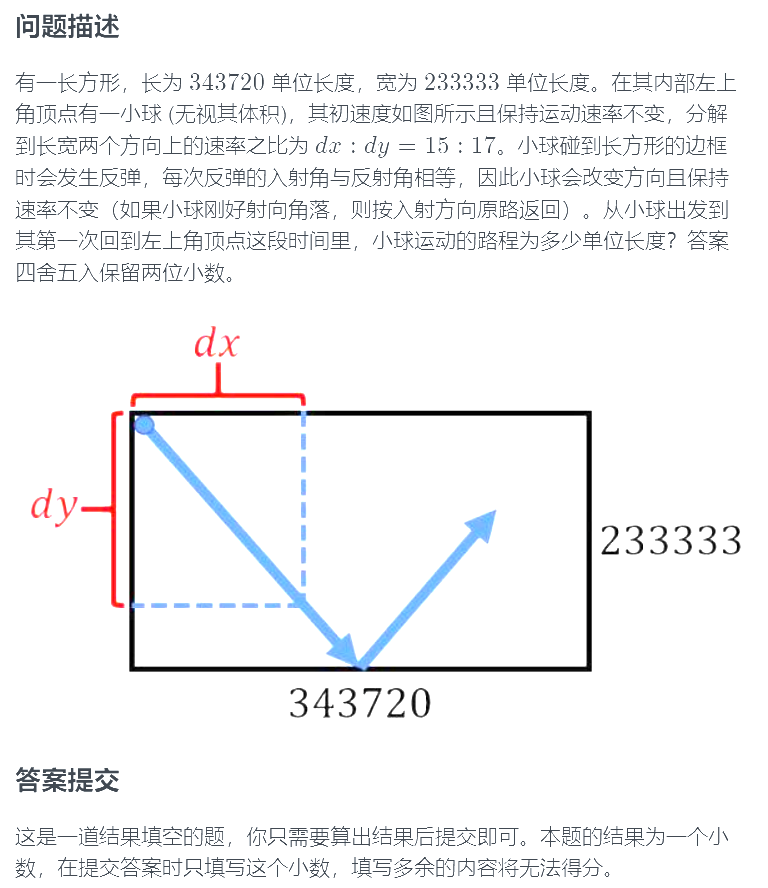
本想暴搜的,看了题解才发现有巧♂妙的数学方法:将长方形无限铺展开,小球每次碰壁后反向,都相当于进入了下一个长方形。因此当x方向路程和y方向路程都能整除长方形的长和宽时,就相当于走了一半,算出距离乘二即可
#include <bits/stdc++.h>
#define int long long
using namespace std;
const int x_ = 343720;
const int y_ = 233333;
signed main(void){
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
int t = 1;
while(1){if((15*t)%x_==0 && (17*t)%y_==0) break;t++;}
cout << fixed << setprecision(2) << 2*sqrt(15*t*15*t+17*t*17*t) << '\n';
return 0;
}
C

暴!
#include <bits/stdc++.h>
using namespace std;
int main(void){
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
int n,sum = 0;
cin >> n;
for(int i=1;i<=n;i++){
int i_=i;
while(i_>0){
if(i_%2) i_/=10;
else break;
if(!(i_%2)) i_/=10;
else break;
if(!i_) sum++;
}
}
cout << sum << '\n';
return 0;
}
D

高精度处理
#include <bits/stdc++.h>
using namespace std;
const int maxn = 2001;
int n,a[maxn]={0},si,poi;
string s;
void check(){
for(int i=1;i<=si;i++){
a[i+1] += a[i]/10;
a[i] %= 10;
}
if(a[si+1]) si++;
}
int main(void){
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
cin >> n >> s;
reverse(s.begin(),s.end());
poi = s.find('.');
s.erase(poi,1);
si = s.size();
//cout << si << '\n';
for(int i=0;i<si;i++)
a[i+1] = s[i]-'0';
for(int i=1;i<=n;i++){
for(int j=1;j<=si;j++)
a[j] *= 2;
check();
}
//for(int i=1;i<=si;i++) cout << a[i];
//cout << '\n';
if(a[poi]>=5){
a[poi+1]++;
check();
}
//cout << poi << ' ' << si << '\n';
for(int i=si;i>poi;i--)
cout << a[i];
cout << '\n';
return 0;
}
E

题目给出的S的公式可以化简,化简后就是三个数的最大公因数。
由于最大公因数的最大者不会超过输入的数据中的最大数,因此先取输入的数据中的最大数h,然后从h到1逐个枚举,当某次枚举可以枚举出3个公因数时就ok
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e5+1;
int a[maxn]={0};
int main(void){
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
int n,h=0;
cin >> n;
for(int i=1;i<=n;i++){
int cache;
cin >> cache;
a[cache]++;
h = max(h,cache);
}
for(int i=h;i>=1;i--){
int sum=0, pos=0, ans[3];
for(int j=i;j<=h;j+=i){
if(a[j]){
sum += a[j];
for(int k=0;k<a[j] && pos<3;k++)
ans[pos++] = j;
}
if(sum >= 3){
for(int i=0;i<3;i++)
cout << ans[i] << ' ';
cout << '\n';
return 0;
}
}
}
return 0;
}
G

先做一个前缀和,然后用multiset维护每个左右区间,当取了左区间后,二分找出右区间内最接近左区间的值,然后取这些值里的最小值
#include <bits/stdc++.h>
#define int long long
using namespace std;
const int midn = 1e3+1;
const int maxn = 1e6+1;
const int sup = 1e15;
const int inf = -1e15;
int a[midn];
multiset <int> ms;
signed main(void){
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
int n;
cin >> n;
for(int i=1;i<=n;i++){
cin >> a[i];
a[i] += a[i-1];
}
ms.insert(sup);
ms.insert(inf);
int ans = 0x3f;
for(int i=1;i<=n;i++){
for(int j=1;j<=i-1;j++)
ms.insert(a[i-1]-a[j-1]);
for(int k=i;k<=n;k++){
int sum = a[k]-a[i-1];
auto it = ms.lower_bound(sum);
ans = min(ans,*it-sum);
--it;
ans = min(ans,sum-*it);
}
}
cout << ans << '\n';
return 0;
}
第14届蓝桥真题
填空AB

这题按常规思路来做麻烦死人,正常人都不想写的。所以要来一个思路转换:枚举2023年的每一个日期,然后判断从这些数里能不能找出这个日期
#include <bits/stdc++.h>
using namespace std;
int main(void){
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
int a[101],sum = 0;
int date[] = {20250410,31,28,31,30,31,30,31,31,30,31,30,31};
for(int i=1;i<=100;i++) cin >> a[i];
for(int m=1;m<=12;m++){
for(int d=1;d<=date[m];d++){
int s[] = {2,0,2,3,m/10,m%10,d/10,d%10};
int cnt = 0;
for(int k=1;k<=100;k++){
if(a[k] == s[cnt]) cnt++;
if(cnt == 8) {sum++;break;}
}
}
}
cout << sum << '\n';
return 0;
}

如题,公式也给了,自己再化个简,然后从1到n/2逐个枚举就行。填空B要比A简单。。。
#include <bits/stdc++.h>
using namespace std;
const double N = 23333333.0;
const double num = 11625907.5798;
double cul(int x,int y){
return -(1.0*x*x/N)*log2(1.0*x/N)-(1.0*y*y/N)*log2(1.0*y/N);
}
int main(void){
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
for(int i=1;i<=11666666;i++){
if(fabs(cul(i,N-i)-num) < 0.0001) cout << i;
}
return 0;
}
C

数学题,想到了(其实很多情况下是猜到了)就简单
#include <bits/stdc++.h>
using namespace std;
int main(void){
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
int n;
cin >> n;
int maxn=0x3f3f3f3f,minn=0;
for(int i=0;i<n;i++){
int a,b;
cin >> a >> b;
maxn = min(maxn,a/b);
minn = max(minn,a/(b+1)+1);
}
cout << minn << ' ' << maxn << '\n';
return 0;
}
D

DFS暴搜,确实是暴力杯的做法
#include <bits/stdc++.h>
using namespace std;
const int maxn = 12;
int start_[maxn] ,end_[maxn], l[maxn], pd = 0, n;
bool vis[maxn];
void dfs(int now,int index,int cnt){
if(now < start_[index]) now = start_[index];
if(!pd && now && now>end_[index]) {
//cout<<"now: "<<now<<" index:"<<index<<" cnt:"<<cnt<<'\n';
return;}
else now+=l[index];
if(now < start_[index]) now = start_[index];
if(cnt == n){
pd = 1;
return;
}
//cout<<"now:"<<now<<" index:"<<index<<" cnt:"<<cnt<<'\n';
for(int i=1;i<=n;i++){
if(!vis[i]){
vis[i] = 1;
//scout << "index:"<<index<<" i:"<<i<<'\n';
dfs(now,i,cnt+1);
vis[i] = 0;
}
}
return;
}
int main(void){
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
int T;
cin >> T;
while(T--){
cin >> n;
pd = 0;
for(int i=1;i<=n;i++){
cin >> start_[i] >> end_[i] >> l[i];
end_[i] += start_[i];
}
dfs(0,0,0);
cout << (pd ? "YES\n" : "NO\n");
}
return 0;
}
E

dp
求最少要删的数的个数,直接求不好求,转换思维,求最长的序列,n减去最长的序列就是最少要删的数的个数。
用dp[i]表示以数字i结尾的最长序列,由于上个数字末尾和这个数字开头一样,因此来的方向是dp[s[0]-'0']。状态转移方程:
dp[s[si-1]-'0'] = max(dp[s[si-1]-'0'],dp[s[0]-'0']+1);
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e5+1;
int dp[10] = {0};
int main(void){
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
int n;
cin >> n;
string s;
for(int i=0;i<n;i++){
cin >> s;
int si = s.size();
dp[s[si-1]-'0'] = max(dp[s[si-1]-'0'],dp[s[0]-'0']+1);
}
int ans = 0;
for(int i=0;i<10;i++)
ans = max(ans,dp[i]);
cout << n-ans << '\n';
return 0;
}
F

篮球杯是真喜欢考逆向思维啊......
常规思路就是判断外岛是否构成环,内岛是否被外岛包围而变成子岛屿,但这样很不好写。逆向思维:一个岛屿不是子岛屿的充要条件是它向八个方向的海水格延伸,可以延伸到地图外去。因此两个bfs,一个把所有当前的岛相连的岛搜出来,另一个判断这堆岛是不是子岛屿。
#include <bits/stdc++.h>
using namespace std;
int n,m,ans;
char room[55][55];
bool vis_i[55][55],vis_s[55][55];
int explore[][2] = {1,0,-1,0,0,1,0,-1,1,1,1,-1,-1,1,-1,-1};
struct node{
int x,y;
};
void bfs_i(int x,int y){
queue <node> q;
q.push({x,y});
vis_i[x][y] = 1;
while(!q.empty()){
node start= q.front();
q.pop();
node next;
for(int i=0;i<4;i++){
next.x = start.x + explore[i][0];
next.y = start.y + explore[i][1];
if(room[next.x][next.y]=='1' && !vis_i[next.x][next.y] && next.x>=1 && next.x<=n && next.y>=1 && next.y<=m){
vis_i[next.x][next.y] = 1;
q.push({next.x,next.y});
}
}
}
}
bool bfs_s(int x,int y){
queue <node> q;
q.push({x,y});
while(!q.empty()){
node start = q.front();
q.pop();
if(start.x<=1 || start.x>=n || start.y<=1 || start.y>=m) return 1;
node next;
for(int i=0;i<8;i++){
next.x = start.x + explore[i][0];
next.y = start.y + explore[i][1];
if(room[next.x][next.y]=='0' && !vis_s[next.x][next.y]){
vis_s[next.x][next.y] = 1;
q.push({next.x,next.y});
}
}
}
return 0;
}
void solve(){
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
if(room[i][j]=='1' && !vis_i[i][j]){
memset(vis_s,0,sizeof(vis_s));
bfs_i(i,j);
if(bfs_s(i,j)) ans++;
}
}
}
}
int main(void){
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
int t;
cin >> t;
while(t--){
memset(vis_i,0,sizeof(vis_i));
ans = 0;
cin >> n >> m;
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
cin >> room[i][j];
solve();
cout << ans << '\n';
}
return 0;
}
欧拉筛(Sieve of Euler)
和欧拉筛相见恨晚啊,以前一直用埃氏筛,这不就有更好的
欧拉筛是一种线性筛,时间复杂度为O(n),求得1~n内所有素数。欧拉筛是对埃氏筛的改进
欧拉筛原理:
一个合数肯定有一个最小质因数;让每个合数只被它的最小质因数筛选一次,以达到不重复筛的目的。
欧拉筛可以处理约n=1e8的问题,bool vis[N]约100MB,因为N=1e8时有5761455个素数,因此int prime[5800000],约23MB,否则大小为N就会超出限制
const int N = 1e8;
int prime[5800000]={0};
bool vis[N]={0};
int euler_sieve(int n){
int cnt = 0; //记录素数个数
for(int i=2;i<=n;i++){
if(!vis[i]) prime[cnt++] = i; //如果没被筛过,是素数,记录
for(int j=0;j<cnt;j++){ //用已得到的素数去筛后面的数
if(i*prime[j] > n) break; //只筛<=n的数
vis[i*prime[j]] = 1; //关键1:用x的最小质因数筛去x
if(i%prime[j] == 0) break; //关键2:如果不是这个数的最小质因数,打断
}
}
return cnt;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号