Python科学计算库读书报告：NumPy、SciPy、Pandas和Matplotlib

1. NumPy基本函数用法
   NumPy是Python中用于科学计算的基础库，提供了强大的多维数组对象和各种派生对象。
   基本数组操作

创建数组

import numpy as np
arr1 = np.array([1, 2, 3, 4, 5]) # 一维数组
arr2 = np.array([[1, 2, 3], [4, 5, 6]]) # 二维数组
zeros_arr = np.zeros((3, 3)) # 3x3全零数组
ones_arr = np.ones((2, 4)) # 2x4全1数组
range_arr = np.arange(0, 10, 2) # 类似range函数

数组运算

a = np.array([1, 2, 3])
b = np.array([4, 5, 6])
print(a + b) # 元素相加 [5 7 9]
print(a * b) # 元素相乘 [4 10 18]
print(np.dot(a, b)) # 点积 32

数组索引和切片

arr = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
print(arr[1, 2]) # 6
print(arr[:, 1]) # 第二列 [2 5 8]
data = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])

print(np.mean(data)) # 平均值 5.0
print(np.median(data)) # 中位数 5.0
print(np.std(data)) # 标准差 2.58198889747
print(np.max(data)) # 最大值 9
print(np.min(data)) # 最小值 1
print(np.sum(data)) # 总和 45
2. SciPy基本函数用法
SciPy是基于NumPy的科学计算库，提供了许多高级数学函数和算法。

线性代数
from scipy import linalg

解线性方程组

A = np.array([[3, 2, 0], [1, -1, 0], [0, 5, 1]])
b = np.array([2, 4, -1])
x = linalg.solve(A, b)
print(x) # [ 2. -2. 9.]

计算行列式

det = linalg.det(A)
print(det) # -5.0

特征值和特征向量

eigenvalues, eigenvectors = linalg.eig(A)
print(eigenvalues) # [ 3.61803399 -1.61803399 1. ]

优化问题
from scipy.optimize import minimize

最小化函数

def rosen(x):
return sum(100.0*(x[1:]-x[:-1]2.0)2.0 + (1-x[:-1])**2.0)

x0 = np.array([1.3, 0.7, 0.8, 1.9, 1.2])
res = minimize(rosen, x0, method='nelder-mead', options={'xtol': 1e-8})
print(res.x) # [1. 1. 1. 1. 1.]
3. Pandas基本函数用法
Pandas提供了高效的数据结构和数据分析工具。

Series和DataFrame
import pandas as pd

创建Series

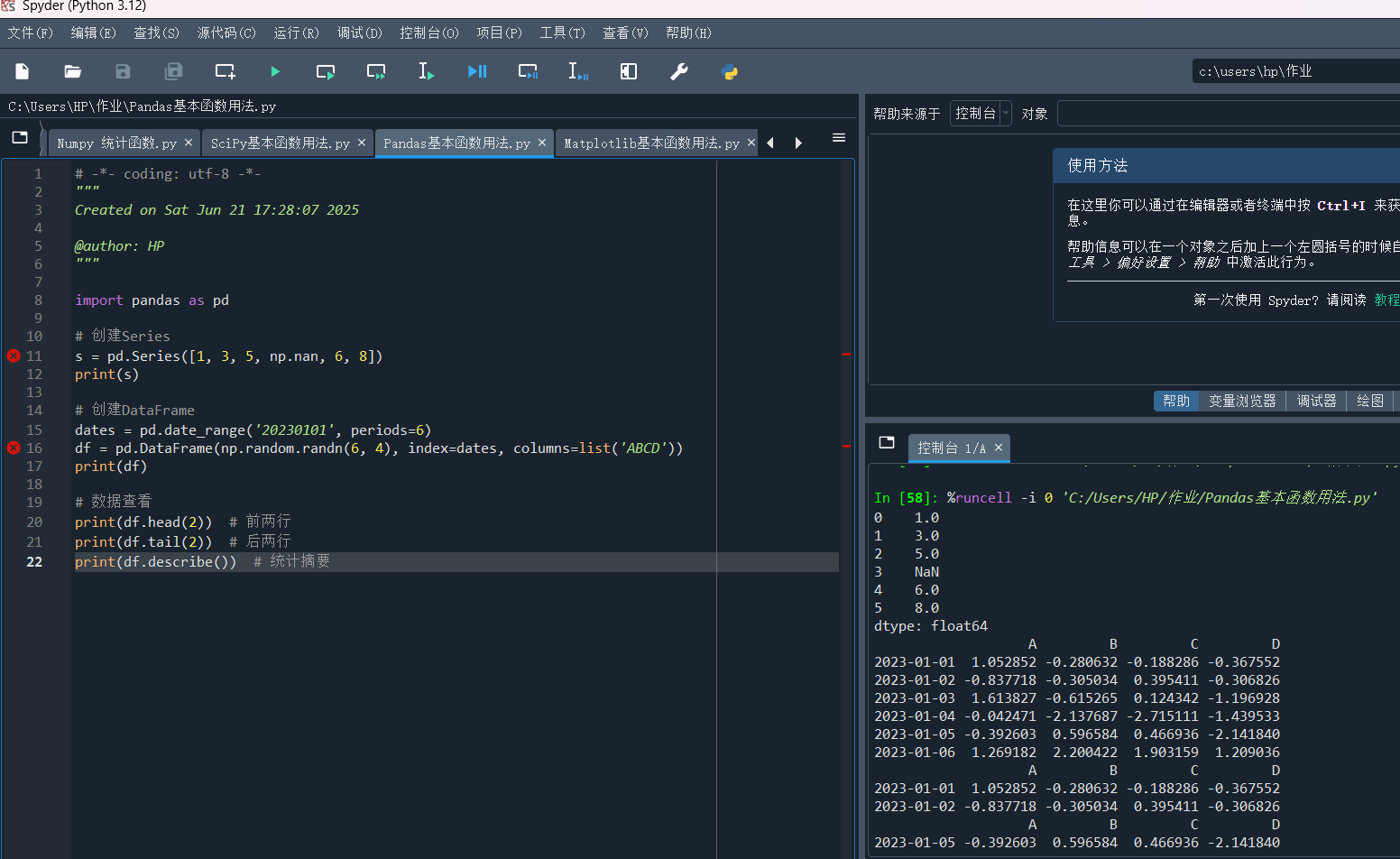
s = pd.Series([1, 3, 5, np.nan, 6, 8])
print(s)

创建DataFrame

dates = pd.date_range('20230101', periods=6)
df = pd.DataFrame(np.random.randn(6, 4), index=dates, columns=list('ABCD'))
print(df)

数据查看

print(df.head(2)) # 前两行
print(df.tail(2)) # 后两行
print(df.describe()) # 统计摘要
数据操作

选择数据

print(df['A']) # 选择A列
print(df[0:3]) # 选择前三行
print(df.loc['20230102':'20230104', ['B', 'C']]) # 按标签选择

数据清洗

df2 = df.copy()
df2['E'] = ['one', 'one', 'two', 'three', 'four', 'three']
print(df2[df2['E'].isin(['two', 'four'])]) # 过滤

分组聚合

print(df2.groupby('E').mean()) # 按E列分组求均值

4. Matplotlib基本函数用法
   Matplotlib是Python中最流行的绘图库。

基本绘图
import matplotlib.pyplot as plt

线图

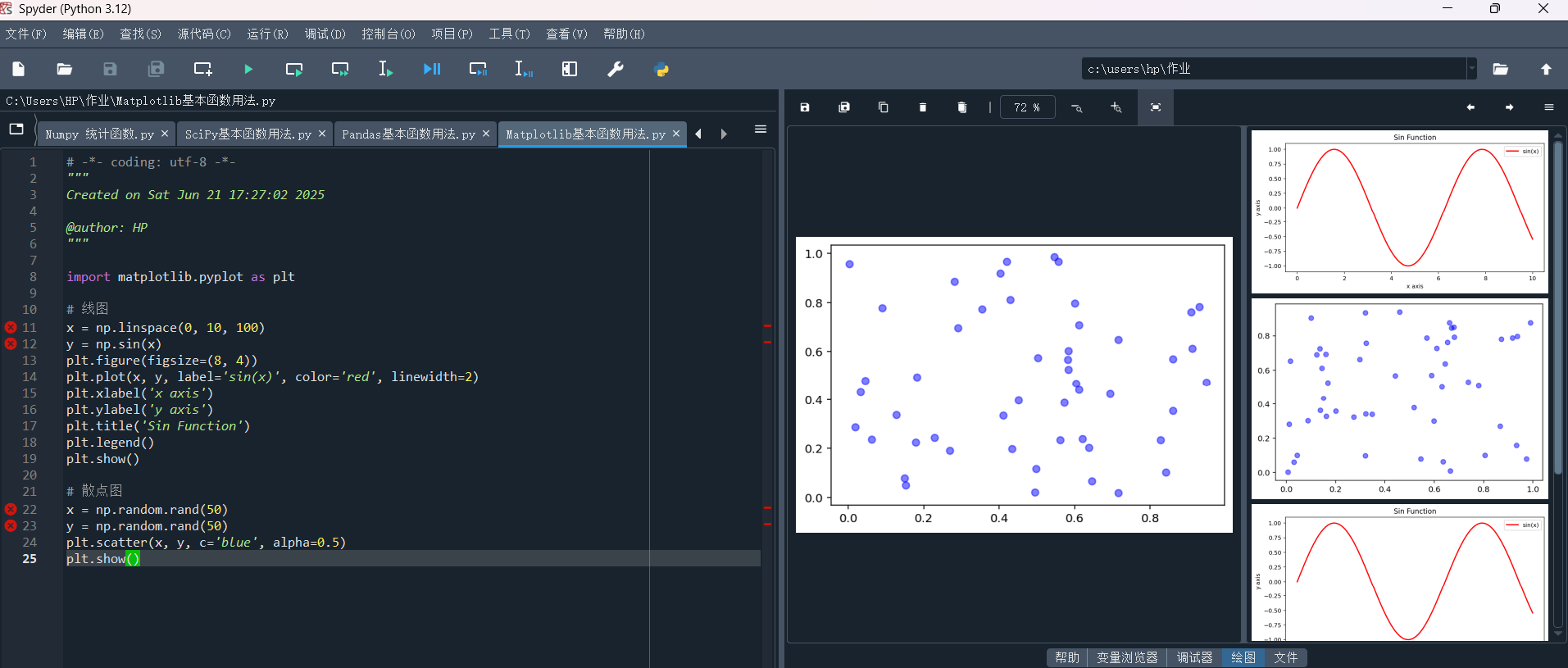
x = np.linspace(0, 10, 100)
y = np.sin(x)
plt.figure(figsize=(8, 4))
plt.plot(x, y, label='sin(x)', color='red', linewidth=2)
plt.xlabel('x axis')
plt.ylabel('y axis')
plt.title('Sin Function')
plt.legend()
plt.show()

散点图

x = np.random.rand(50)
y = np.random.rand(50)
plt.scatter(x, y, c='blue', alpha=0.5)
plt.show()
多子图

创建2x2的子图

fig, axs = plt.subplots(2, 2, figsize=(10, 8))

第一个子图

axs[0, 0].plot(x, np.sin(x))
axs[0, 0].set_title('Sin')

第二个子图

axs[0, 1].plot(x, np.cos(x), 'r--')
axs[0, 1].set_title('Cos')

第三个子图

axs[1, 0].plot(x, np.tan(x), 'g-.')
axs[1, 0].set_title('Tan')

第四个子图

axs[1, 1].plot(x, np.exp(x), 'b:')
axs[1, 1].set_title('Exp')

plt.tight_layout()
plt.show()

5. 具体问题求解示例
   求解线性回归问题

使用NumPy求解线性回归

X_b = np.c_[np.ones((100, 1)), X] # 添加x0=1
theta_best = np.linalg.inv(X_b.T.dot(X_b)).dot(X_b.T).dot(y)
print("最佳参数:", theta_best) # 接近[4, 3]

绘制结果

plt.scatter(X, y)
plt.plot(X, X_b.dot(theta_best), 'r-')
plt.xlabel('X')
plt.ylabel('y')
plt.title('线性回归')
plt.show()
求解微分方程
from scipy.integrate import odeint

定义微分方程

def model(y, t):
k = 0.3
dydt = -k * y
return dydt

初始条件

y0 = 5

时间点

t = np.linspace(0, 20, 100)

求解ODE

y = odeint(model, y0, t)

绘图

plt.plot(t, y)
plt.xlabel('time')
plt.ylabel('y(t)')
plt.title('一阶微分方程求解')
plt.show()
6. 图像处理示例
使用NumPy和Matplotlib进行图像处理
from scipy import misc

生成一个简单的图像

face = misc.face(gray=True)
plt.imshow(face, cmap=plt.cm.gray)
plt.title('原始图像')
plt.show()

图像反转

inverted_face = np.invert(face)
plt.imshow(inverted_face, cmap=plt.cm.gray)
plt.title('反转图像')
plt.show()

边缘检测

from scipy import ndimage

Sobel边缘检测

sx = ndimage.sobel(face, axis=0, mode='constant')
sy = ndimage.sobel(face, axis=1, mode='constant')
sobel = np.hypot(sx, sy)

plt.imshow(sobel, cmap=plt.cm.gray)
plt.title('Sobel边缘检测')
plt.show()
图像滤波
from scipy.ndimage import gaussian_filter

高斯模糊

blurred_face = gaussian_filter(face, sigma=3)
plt.imshow(blurred_face, cmap=plt.cm.gray)
plt.title('高斯模糊')
plt.show()

中值滤波

noisy_face = face + 0.5 * face.std() * np.random.random(face.shape)
median_face = ndimage.median_filter(noisy_face, size=3)
plt.imshow(median_face, cmap=plt.cm.gray)
plt.title('中值滤波去噪')
plt.show()
总结
本报告介绍了Python中四个重要的科学计算库：NumPy、SciPy、Pandas和Matplotlib的基本用法，并通过具体示例展示了它们在数值计算、数据分析、可视化和图像处理方面的应用。这些库共同构成了Python科学计算生态系统的基础，为数据科学、机器学习和工程计算提供了强大的工具支持。

通过掌握这些库的基本函数和高级功能，可以高效地解决各种科学计算问题，从简单的数组操作到复杂的数学建模和数据分析任务。在实际应用中，这些库通常结合使用，发挥各自的优势，为数据分析和科学研究提供全面的解决方案。