算法设计与分析课-实验-分治
算法设计与分析
第一题
暴力法
众数问题:【问题描述】给定含有S个元素的多重集合S,每个元素在S中出现的次数称为该元素的重数。多重集S中重数最大的元素称为众数。例如,S={1,2,2,2,3,5}。多重数S的众数是2,其重数为3 。
【算法设计】对于给定的由n个自然数组成的多重集S,计算S的众数及其重数。
【输入形式】第1行为多重数集S中元素个数n;接下来的n行中,每行有一个自然数。
【输出形式】输出文件有2行,第1行是众数,第2行是重数。
【样例输入】
6
1
2
2
2
3
5
【样例输出】
2
3
#include<iostream>
#define MAXSIZE 100+5
using namespace std;
typedef struct
{
int num;
int count;
}Node;
Node func()
{
int n;
cin>>n;
int S[MAXSIZE];
Node node[MAXSIZE];
for(int i=0; i<MAXSIZE; ++i)
{
node[i].count=0;
node[i].num=-1;
}
int num=0, count=0, k=0;
for(int i=0; i<n; ++i)
{
cin>>S[i];
if(i==0)
{
node[k].num=S[i];
node[k].count++;
}
else
{
if(node[k].num==S[i])
{
node[k].count++;
}
else
{
node[++k].num=S[i];
node[k].count++;
}
}
}
for(int i=0; i<=k; ++i)
{
if(count<node[i].count)
{
num=node[i].num;
count=node[i].count;
}
}
Node p;
p.count=count;
p.num=num;
return p;
}
int main()
{
Node p = func();
cout<<p.num<<endl;
cout<<p.count<<endl;
return 0;
}
分治法
分治法思路:将整个问题分解成若干个子问题后在解决,如果得到的子问题还是很大,则可以反复利用分治策略将这些子问题分解成更小的子问题,直到便于进行求解,必要时逐步合并这些子问题的解,从而得到问题的解。分治算法可以由递归过程来表示,因为分治法就是一种找大规模问题与小规模问题关系的方法,是递归设计的一种具体策略。(copy的)
该问题中,先假设第一个数为众数,将不小于它的移到它的右边,不大于它的移到它的左边,然后以该数(即key)为分界,分别求解其左边和右边的众数,最后进行比较得解。
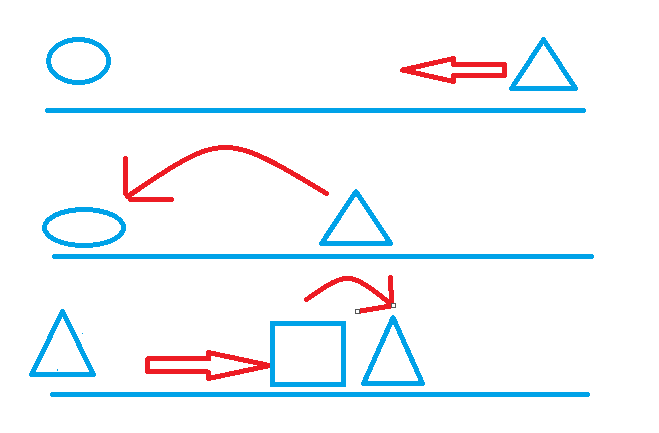
从high1往左开始,找到小于key的,把它放到low1位置(此时数组中多了一个high1位的值,少了key),然后从low1位置开始往右,找到大于key的,把它放到high1(此时high1位的值被换成了low1位的值,消掉了,但low1位的值重复了),最后low1等于high1的时候把key放到low1位置(恢复了key,消掉了重复的),则查找完成。
#include<iostream>
#define maxn 100+5
using namespace std;
//分治法
typedef struct Node
{
int num;
int count;
}Node;
Node getMax(Node a, Node b, Node c)
{
Node tmp;
tmp.num=0;
tmp.count=0;
if(a.count>b.count)
{
tmp=a;
}
else
{
tmp=b;
}
if(c.count>tmp.count)
{
tmp=c;
}
return tmp;
}
Node getMany(int a[], int length, int low, int high)
{
Node p,p1,p2;
p.num=a[low];//假设众数为第一个
p.count=1;
if(low<high)
{
int key=a[low];
int tmp;
int low1=low, high1=high;
while(low1<high1)
{
while(low1<high1&&a[high1]>=key)//从右边不小于key的找与key相等的,找到比key小的将其换到low1
{
if(a[high1]==key)
{
p.count++;
}
high1--;
}
a[low1]=a[high1];
while(low1<high1&&a[low1]<=key)//从左边不大于key的找与key相等的,找到比key大的将其换到high1
{
if(a[low1]==key)
{
p.count++;
}
low1++;
}
a[high1]=a[low1];
}
a[low1]=key;//换到最后low1等于high1,把key换到low1,此时key1左边都是不大于它的,右边都是不小于它的
int index=low1;
p1=getMany(a,length,low,index-1);
p2=getMany(a,length,index+1,high);
p=getMax(p,p1,p2);
}
return p;
}
int main()
{
int n;
cin>>n;
int a[maxn];
for(int i=0; i<n; i++)
{
cin>>a[i];
}
Node ans;
ans=getMany(a, n, 0, n-1);
cout<<ans.num<<" "<<ans.count<<endl;
return 0;
}
第二题
双色汉诺塔问题:【问题描述】设 A、B、C 是 3 个塔座。开始时,在塔座 A 上有一叠共 n 个圆盘,这些圆盘自下而上, 由大到小地叠在一起。各圆盘从小到大编号为 1,2,……,n,奇数号圆盘着蓝色,偶数号圆盘着红色,如图所示。现要求将塔座 A 上的这一叠圆盘移到塔座 B 上,并仍按同样顺序叠置。在移动圆盘时应遵守以下移动规则:
规则(1):每次只能移动 1 个圆盘;
规则(2):任何时刻都不允许将较大的圆盘压在较小的圆盘之上;
规则(3):任何时刻都不允许将同色圆盘叠在一起;
规则(4):在满足移动规则(1)-(3)的前提下,可将圆盘移至 A,B,C 中任一塔座上。
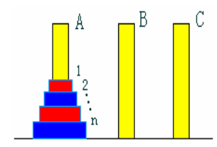
【输入形式】输入圆盘个数n
【输出形式】每一行由一个正整数 k 和 2 个 字符 c1 和 c2 组成,表示将第 k 个圆盘从塔座 c1 移到塔座 c2 上
#include<iostream>
using namespace std;
void move_hanoi(char A, char B, int n)
{
cout<<n<<" "<<A<<" "<<B<<endl;
}
void Hanoi(char A, char B, char C, int n)
{
if(n==1)
{
move_hanoi(A,C,n);
return ;
}
Hanoi(A, C, B, n-1);
move_hanoi(A,C,n);
Hanoi(B, A, C, n-1);
}
/*
先把前n-1个圆盘借助C移动到B上,再把第n个圆盘移动到C上
然后把前n-1个圆盘借助A移动到C上
*/
int main()
{
int n;
cin>>n;
Hanoi('A','B','C',n);
return 0;
}
第三题
半数集问题:

半数集即对于给定的一个数,在它的左边加上一个数,但是新加上的数不超过最近添加的数的一半,得到的所有数组成的集合就是半数集。以本题为例,求解6的半数集。
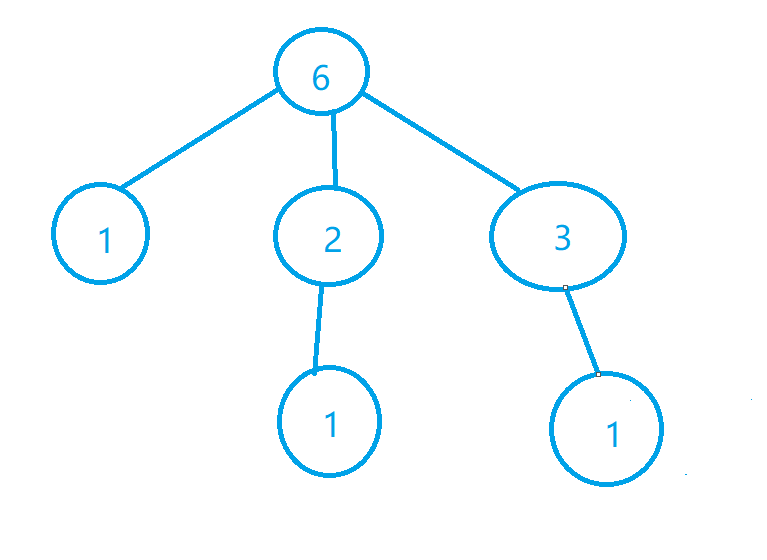
如图所示,在6的左边可以加1、2、3,在2、3的左边又可以分别加个1,所以6的半数集为{6,16,26,36,126,136}。利用分治的思想,求一个数的半数集元素个数就是求不超过该数一半的数的半数集的元素个数的和,只需递归的求解问题即可。
#include<iostream>
using namespace std;
int halfNum(int n)
{
int ans=1;
for(int i=1; i<=n/2; ++i)
{
ans+=halfNum(i);
}
return ans;
}
int main()
{
int n;
cin>>n;
cout<<halfNum(n)<<endl;
return 0;
}
最后还要加上该数自己,也即最初给ans赋值为1。
第四题
逆序对问题:

对于给定的数组,逆序对的定义就是对于两个元素A[i]和A[j],A[i]>A[j]且i<j,即左边的值大于右边的值得就是逆序对。
简单的解法就是用嵌套的for循环,遍历数组一个一个比较,但这种方法的时间复杂度为O(n2)。
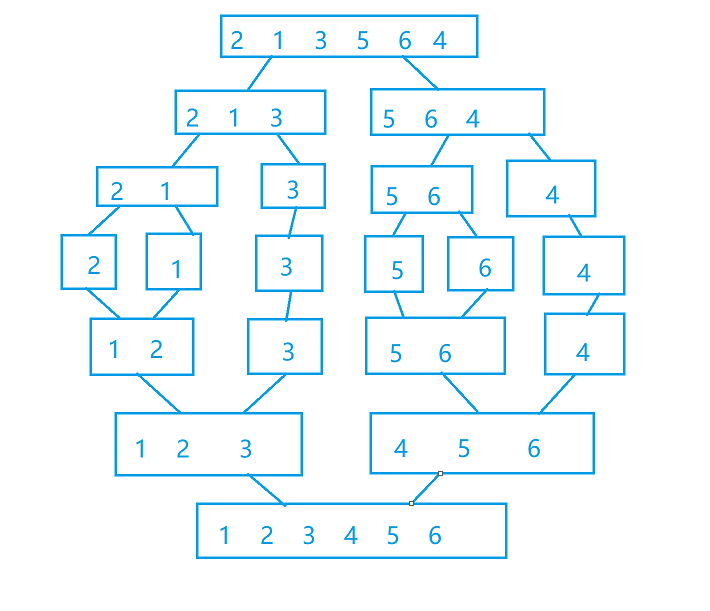
分治的思想为将原问题分解为若干个子问题,先求子问题中的逆序对,再不断合并子问题再求逆序对。
但是合并子问题再去求逆序对还是需要遍历合并的序列去求逆序对,这样时间复杂度还是一样。解决办法为:因为求解子问题的逆序对的过程中,子问题的序列中的逆序对已经找到了,再合并子问题去求逆序对的时候就是找该序列与另一个序列中的元素组成的逆序对了,那么可以将该子问题的序列排序,这样在合并子问题进行查找的时候就可以从左右子序列的最后一位开始比较了。(因为最后一位是最大的,如果能构成逆序对,说明该元素和右边序列当前位置及其之前的所有元素都能组成逆序对)
#include<iostream>
//#define maxn 1000000+5
#define maxn 500000+5
using namespace std;
int merge(int a[], int temp[], int left, int mid, int right);
int antiPair(int a[], int temp[], int left, int right);
int main()
{
int n; cin>>n;
int A[maxn], temp[maxn];
for(int i=0; i<n; ++i) cin>>A[i];
cout<<antiPair(A, temp, 0, n-1);
return 0;
}
long long merge(int a[], int temp[], int left, int mid, int right)
{
int count=0;
for(int i=left; i<=right; ++i)
{
temp[i]=a[i];
}
int k=right;
for(int i=mid, j=right; i>=left&&j>=mid+1; )
{
if(temp[i]>temp[j])
{
//count+=j-mid-2; 错误
count+=j-mid;
a[k--]=temp[i--];
}
else
{
a[k--]=temp[j--];
}
if(i<left)
{
while(j>=mid+1)
{
a[k--]=temp[j--];
}
}
else if(j<mid+1)
{
while(i>=left)
{
a[k--]=temp[i--];
}
}
}
return count;
}
int antiPair(int a[], int temp[], int left, int right)
{
if(left == right)
{
return 0;
}
int mid = (left + right) / 2;
int suml=antiPair(a, temp, left, mid);
int sumr=antiPair(a, temp, mid+1, right);
int sumlr=merge(a, temp, left, mid, right);
return suml+sumr+sumlr;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号