归并排序C++实现

把归并排序看作二叉树的后序遍历的确是一种好的思路，使代码的逻辑更加清晰。

但是具体实现还是遇到了很多的困难。

有太多报错，自己也觉得有些莫名其妙。但是事后看来，大多数还是自己粗心所致。

以后都可以采用这个框架来处理需要归并排序的问题。

class Solution {
public:
    vector<int> temp;
    std::vector<int> sortArray(std::vector<int>& nums) {
        temp.resize(nums.size());
        mergeSort(nums, 0, nums.size() - 1);
        return nums;
    }
 
    void mergeSort(std::vector<int>& nums, int low, int high) {
        if (low >= high) return;
        int mid = low + (high - low) / 2;
        mergeSort(nums, low, mid);
        mergeSort(nums, mid + 1, high);
        merge(nums, low, mid, high);
    }
 
    void merge(std::vector<int>& arr, int low, int mid, int high) {
        for (int i = low; i <= high; i++) {
            temp[i] = arr[i];
        }
        int i = low, j = mid + 1;
        for (int p = low; p <= high; p++) {
            if (i == mid + 1) {
                arr[p] = temp[j++];
            } else if (j == high + 1) {
                arr[p] = temp[i++];
            } else if (temp[i] > temp[j]) {
                arr[p] = temp[j++];
            } else {
                arr[p] = temp[i++];
            }
        }
    }
};

活用：利用归并排序计算右侧小的元素数量。乐扣315。
同样的框架：关键在于两个细节。

1. 重复元素的指针移动问题，根据题目要求题目要求是小于，移动左指针。
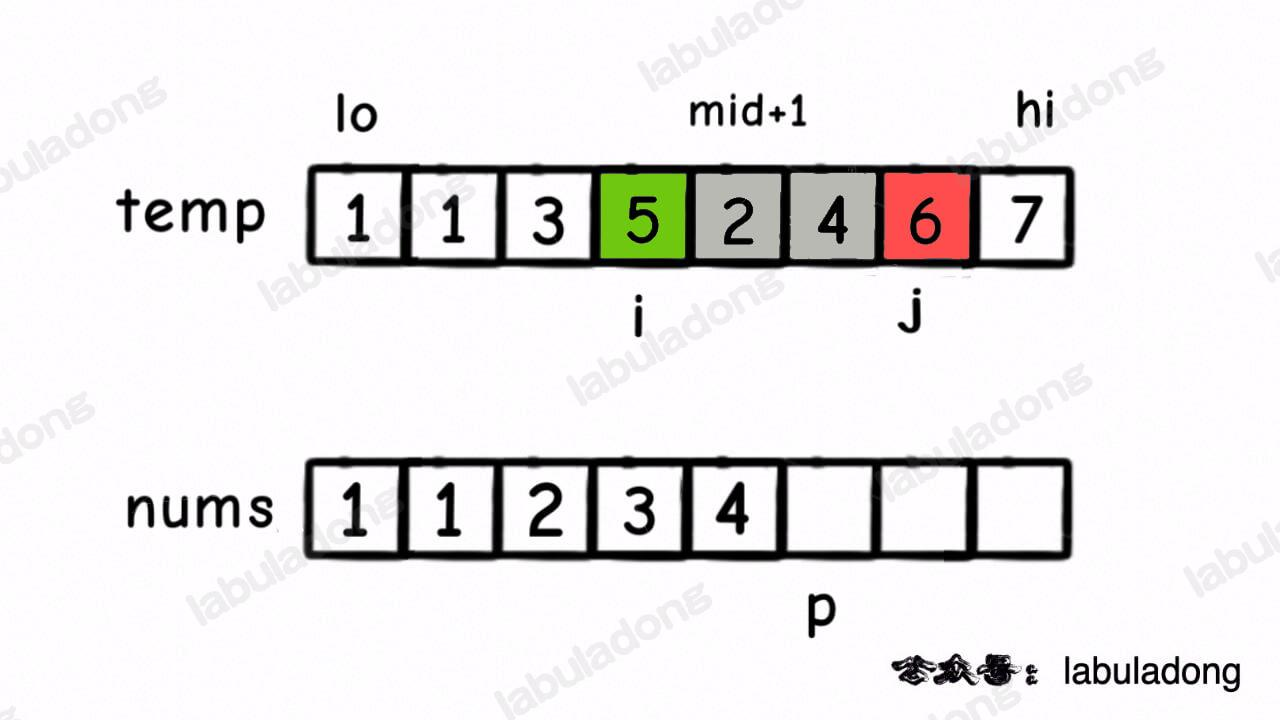
2. 在对 nuns[lo..hi] 合并的过程中，每当执行 nums[p] = temp[i] 时，就可以确定 temp[i] 这个元素后面比它小的元素个数为 j - mid - 1。
   

class Solution {
private:
    // 归并排序所用的辅助数组
    vector<pair<int, int>> temp;
    // 记录每个元素后面比自己小的元素个数
    vector<int> count;
 
public:
    // 主函数
    vector<int> countSmaller(vector<int>& nums) {
        int n = nums.size();
        count.resize(n);
        temp.resize(n);
        vector<pair<int, int>> arr;
        // 记录元素原始的索引位置，以便在 count 数组中更新结果
        for (int i = 0; i < n; i++)
            arr.push_back({nums[i], i});
 
        // 执行归并排序，本题结果被记录在 count 数组中
        mergeSort(arr, 0, n - 1);
 
        return count;
    }
 
private:
    // 归并排序
    void mergeSort(vector<pair<int, int>>& arr, int lo, int hi) {
        if (lo >= hi) return;
 
        int mid = lo + (hi - lo) / 2;
        mergeSort(arr, lo, mid);
        mergeSort(arr, mid + 1, hi);
        merge(arr, lo, mid, hi);
    }
 
    // 合并两个有序数组
    void merge(vector<pair<int, int>>& arr, int lo, int mid, int hi) {
        for (int i = lo; i <= hi; i++) {
            temp[i] = pair(arr[i].first, arr[i].second);
        }
 
        int i = lo, j = mid + 1;
        for (int p = lo; p <= hi; p++) {
            if (i == mid + 1) {
                arr[p] = temp[j++];
            } else if (j == hi + 1) {
                arr[p] = temp[i++];
                // 更新 count 数组
                count[arr[p].second] += j - mid - 1;
            } else if (temp[i].first > temp[j].first) {
                arr[p] = temp[j++]; 
            } else {
                arr[p] = temp[i++];
                // 更新 count 数组
                count[arr[p].second] += j - mid - 1;
            }
        }
    }
};

参考：归并排序详解及应用