lxl 数据结构(一)(2)
书接上回。Link。
Day 3 莫队 + 根号分治
20231204
根号数据结构 /kk
当天下午去补 cf 去了,于是没补题。
Keynote
莫队算法其实是包含了很多的数据结构算法,lxl:这是我最擅长的板块。
莫队相当于 二维扫描线,它是有两个自由度的。
而我们普通的扫描线其实也相当于一个 前缀莫队,所以莫队是包含扫描线的。
而莫队解决的问题就是没有办法同时降两维的问题,也就是 区间不独立。
具体来说,
类似于区间颜色数,区间小 Z 的袜子,和区间逆序对。
这些贡献都是于区间本身相关,是扫描线不能完成的,这个时候就只能用莫队完成。
而把莫队拍到树上,就会变成两个东西:树上莫队 和 子树莫队。
子树莫队 说简单一点就是 dsu on tree,它是可以以 \(\mathcal O(n \log n)\) 时间完成的。
关于莫队的复杂度,具体来说是 \(\mathcal O(n \sqrt m+m)\) 的,前者为修改复杂度,后者为查询复杂度。
而在具体的做题当中,
差分 是一种很重要的思想,它可以 无代价地降低自由度,从而使得问题更好处理。
而差分又不只是前缀差分,还可以是后缀差分,后面有道题会用到。
再来讲一讲 区间子区间 问题,
我们在 Day 2 中已经知道可以用扫描线完成了,
而区间子区间的另一种解决方案就是 莫队 + 差分,后面的题目也会涉及到。
莫队还有一个应用就是 回滚莫队,
其实它于普通莫队的时间最多是 \(\log\) 的,因为回滚莫队就相当于把莫队线段树分治一下。
关于 分块和莫队 有很多小技巧,
感觉课上用的最多的就是去均摊时间。
比如修改的时候莫队的时间已经是 \(n \sqrt m\),为了使整个复杂度不带 \(\log\),
我们可以使用分块去做到 \(\mathcal O(1)\) 修改和 \(\mathcal O(\sqrt n)\) 查询。
这样就可以把时间复杂度变成 \(\mathcal O(n \sqrt m+m \sqrt n)\)。
而对于那些插入代价非 \(\mathcal O(1)\) 的题目,我们可以考虑拆点使得插入的代价变成 \(\mathcal O(1)\)。
很多时候我们还会去 改变块的长度去均摊复杂度,或许在后面也会用到。
还有一个很重要的东西是:
矩阵乘法归约。
感觉还挺有意思的,可以证明一些算法的时间复杂度一定高于矩阵乘法的时间复杂度。
这里讲一个例子:
我们设这里有一个代码
std.cpp,它是用来解决 树上多次询问路径颜色数的。现在我们考虑矩阵乘法,构造两个矩阵 \(A,B\),我们令我们把这两个矩阵丢给
std.cpp,它可以帮我们算出 \(A \times B = C\)。这里我们钦定 \(A,B\) 的值域都是 \([0,1]\) 的,(如果不是也是可以完成的,就相当于进行一个二进制的拆位)
那么现在考虑如何转化?
我们设矩阵是 \(\sqrt n \times \sqrt n\) 的,
于是我们去构造一棵树,使得它有 \(\sqrt n\) 条链且每条链都是 \(\sqrt n\) 个节点。
那么 \(A_{i,j}\) 表示第 \(i\) 条链是否有第 \(j\) 种颜色。
同理我们将 \(B\) 矩阵转置后也像这样表示到一棵树上面,
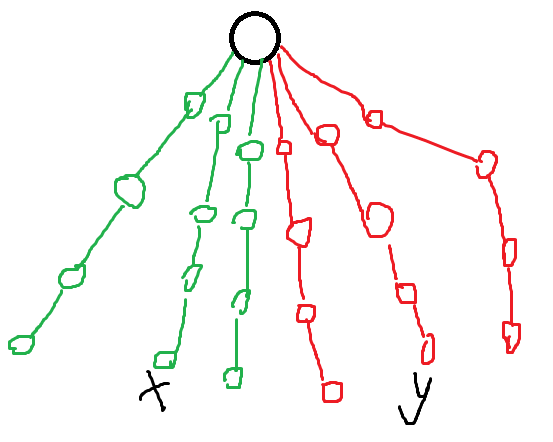
这棵树就成了这样:
绿色和红色分别表示 \(A,B\) 矩阵所构成的链。
现在我们考虑进行 \(n\) 次询问,
每一次询问绿色的端点 \(x\) 到红色的端点 \(y\) 上面的颜色数。
令得到的矩阵是 \(C\),
那么
\[C_{x,y} = \sum_{i=1}^\sqrt n A_{x,i} | B_{i,y} \]由于我们的 \(B\) 是转置后才映射到图上面的,所以是正确的。
发现这个形式和矩阵乘法很像,而 \(|\) 可以等价于 \(\times\)。
而 \(\sqrt n \times \sqrt n\) 矩阵乘法的时间复杂度是 \(\mathcal O(n \sqrt n)\) 的,
所以我们可以证明到这个问题的时间复杂度是 \(\ge n \sqrt n\) 的。
很多问题都可以被这里的矩阵乘法归约掉,这里其他的不做详细介绍,lxl PPT 上面该是有的。
前置题目 P1494 小 Z 的袜子
在 lxl 口中这似乎已经不是一道题,而是一类问题的名字。
给出一个长度为 \(n\) 的序列 \(a\)。
\(m\) 次询问每次求区间 \([l,r]\) 中有多少 \(i,j\) 满足 \(a_i = a_j\)。
\(1 \le n,m \le 5 \times 10^4\)。
还是比较容易的一道题目。
设 \(c\) 数组表示每一种颜色的出现次数,
那么我们其实就是求
于是直接用莫队维护一下每个颜色的个数平方和即可。
Code
#include <bits/stdc++.h>
using namespace std;
#define ll long long
const int N=1e6+5;
int n,m,a[N],c[N],bl[N],B,l,r;
ll ans;
struct node{
int l,r,id;
bool operator <(const node &rhs) const{
if(bl[l]!=bl[rhs.l]) return bl[l]<bl[rhs.l];
return r<rhs.r;
}
}q[N];
struct Answer{ll a,b;}p[N];
ll gcd(ll x,ll y){
if(y==0) return x;
return gcd(y,x%y);
}
void chg(int x,int v){
if(x==0) return;
ans-=1ll*c[a[x]]*c[a[x]];
c[a[x]]+=v;
ans+=1ll*c[a[x]]*c[a[x]];
}
int main(){
/*2023.12.5 H_W_Y P1494 [国家集训队] 小 Z 的袜子 fk*/
ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
cin>>n>>m;B=(int)floor(sqrt(n));
for(int i=1;i<=n;i++) cin>>a[i],bl[i]=(i-1)/B+1;
for(int i=1;i<=m;i++) cin>>q[i].l>>q[i].r,q[i].id=i;
sort(q+1,q+m+1);l=r=0;ans=0;
for(int i=1;i<=m;i++){
if(q[i].l==q[i].r){p[q[i].id]=(Answer){0,1};continue;};
while(r<q[i].r) chg(++r,1);
while(l>q[i].l) chg(--l,1);
while(r>q[i].r) chg(r--,-1);
while(l<q[i].l) chg(l++,-1);
ll g=gcd(ans-1ll*(q[i].r-q[i].l+1),1ll*(q[i].r-q[i].l+1)*(q[i].r-q[i].l));
p[q[i].id].a=(ans-1ll*(q[i].r-q[i].l+1))/g;
p[q[i].id].b=1ll*(q[i].r-q[i].l+1)*(q[i].r-q[i].l)/g;
}
for(int i=1;i<=m;i++) cout<<p[i].a<<'/'<<p[i].b<<'\n';
return 0;
}
P4396 [AHOI2013] 作业 - 莫队基础
查询区间 \([l,r]\) 中值在 \([a,b]\) 内的不同数个数。
\(1 \le n,m \le 10^5\)。
首先容易想到对于 \([l,r]\) 进行莫队,
而对于 \([a,b]\),我们可以用树状数组维护,但是这样会多一个 \(\log\)。
所以我们考虑分块值域做到 \(\mathcal O(1)\) 修改。
于是就做完了,时间复杂度 \(\mathcal O(n \sqrt m)\)。
Code
#include <bits/stdc++.h>
using namespace std;
const int N=1e5+5;
int n,m,a[N],bl[N],B,c[N],b[N],l,r,B2;
struct fk{int num,s;}t[N],ans[N];
struct node{
int l,r,a,b,id;
bool operator <(const node &rhs) const{
if((l/B2)!=(rhs.l/B2)) return (l/B2)<(rhs.l/B2);
return r<rhs.r;
}
}q[N];
void ins(int x){
c[x]++;if(c[x]==1) t[bl[x]].num++;
t[bl[x]].s++;
}
void del(int x){
c[x]--;if(c[x]==0) t[bl[x]].num--;
t[bl[x]].s--;
}
fk calc(int L,int R){
fk res=(fk){0,0};
for(int i=L;i<=min(R,bl[L]*B);++i) res.num+=(c[i]>0),res.s+=c[i];
if(bl[L]==bl[R]) return res;
for(int i=(bl[R]-1)*B+1;i<=R;++i) res.num+=(c[i]>0),res.s+=c[i];
for(int i=bl[L]+1;i<bl[R];++i) res.num+=t[i].num,res.s+=t[i].s;
return res;
}
int main(){
/*2023.12.5 H_W_Y P4396 [AHOI2013] 作业 md*/
ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
cin>>n>>m;B=sqrt(100000),B2=(int)sqrt(n);
for(int i=1;i<=100000;i++) bl[i]=(i-1)/B+1;
for(int i=1;i<=n;i++) cin>>a[i],b[i]=a[i];
for(int i=1;i<=m;i++) cin>>q[i].l>>q[i].r>>q[i].a>>q[i].b,q[i].id=i;
sort(q+1,q+m+1);l=1,r=0;
for(int i=1;i<=m;i++){
while(r<q[i].r) ins(a[++r]);
while(l>q[i].l) ins(a[--l]);
while(r>q[i].r) del(a[r--]);
while(l<q[i].l) del(a[l++]);
ans[q[i].id]=calc(q[i].a,q[i].b);
}
for(int i=1;i<=m;i++) cout<<ans[i].s<<' '<<ans[i].num<<'\n';
return 0;
}
CF617E XOR - 莫队基础 + 区间子区间
CF617E XOR and Favorite Number
给定一个长度为 \(n\) 的序列 \(a\),然后再给一个数字 \(k\),再给出 \(m\) 组询问,每组询问给出一个区间,求这个区间里面有多少个子区间的异或值为 \(k\)。
\(1 \le n,m \le 10 ^ 5\),\(0 \le k,a_i \le 10^6\),\(1 \le l_i \le r_i \le n\)。
区间子区间 问题,我们用莫队处理。
首先做一个差分,也就是维护异或的前缀和。
于是每一次插入一个数的时候我们就加上 \(x \oplus k\) 的出现次数,于是直接用莫队维护就可以了。
Code
#include <bits/stdc++.h>
using namespace std;
#define ll long long
const int N=1e5+5,M=1048577;
int n,m,k,a[N],c[M],B,l,r;
ll ans[N],res=0;
struct node{
int l,r,id;
bool operator <(const node &rhs) const{
if((l/B)!=(rhs.l/B)) return (l/B)<(rhs.l/B);
return r<rhs.r;
}
}q[N];
void ins(int x){res+=1ll*c[x^k];c[x]++;}
void del(int x){c[x]--,res-=1ll*c[x^k];}
int main(){
/*2023.12.5 H_W_Y CF617E XOR and Favorite Number md*/
ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
cin>>n>>m>>k;B=sqrt(n);
for(int i=1;i<=n;i++) cin>>a[i],a[i]^=a[i-1];
for(int i=1;i<=m;i++) cin>>q[i].l>>q[i].r,q[i].l--,q[i].id=i;
sort(q+1,q+m+1);l=0,r=-1;
for(int i=1;i<=m;i++){
while(r<q[i].r) ins(a[++r]);
while(l>q[i].l) ins(a[--l]);
while(r>q[i].r) del(a[r--]);
while(l<q[i].l) del(a[l++]);
ans[q[i].id]=res;
}
for(int i=1;i<=m;i++) cout<<ans[i]<<'\n';
return 0;
}
P5268 莫队基础
给你一个长度为 \(N\) 的序列 \(a_i\),\(1\leq i\leq N\),和 \(q\) 组询问,每组询问读入 \(l_1,r_1,l_2,r_2\),需输出
\[\sum\limits_{x=0}^\infty \text{get}(l_1,r_1,x)\times \text{get}(l_2,r_2,x) \]$ \text{get}(l,r,x)$ 表示计算区间 \([l,r]\) 中,数字 \(x\) 出现了多少次。
\(1 \le N \le 5 \times 10^4,1 \le a_i \le N\)。
差分之后直接用莫队维护即可。
具体就是按照前缀差分一下——真没什么好讲的。
实现的时候分别维护 \(l,r\) 的前缀中每一个数的出现次数即可。
Code
#include <bits/stdc++.h>
using namespace std;
#define ll long long
const int N=2e5+5;
int n,m,cnt=0,cl[N],cr[N],l,r,a[N],B;
ll ans[N],res=0;
struct node{
int l,r,id,op;
bool operator <(const node &rhs) const{
if((l/B)!=(rhs.l/B)) return (l/B)<(rhs.l/B);
return r<rhs.r;
}
}q[N];
void ml(int x){
if(x==1) ++l,cl[a[l]]++,res+=cr[a[l]];
else cl[a[l]]--,res-=cr[a[l]],--l;
}
void mr(int x){
if(x==1) ++r,cr[a[r]]++,res+=cl[a[r]];
else cr[a[r]]--,res-=cl[a[r]],--r;
}
int main(){
/*2023.12.5 H_W_Y P5268 [SNOI2017] 一个简单的询问 md*/
ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
cin>>n;B=sqrt(n);
for(int i=1;i<=n;i++) cin>>a[i];
cin>>m;
for(int i=1,l1,l2,r1,r2;i<=m;i++){
cin>>l1>>r1>>l2>>r2;
q[++cnt]=(node){r1,r2,i,1};
q[++cnt]=(node){r1,l2-1,i,-1};
q[++cnt]=(node){l1-1,r2,i,-1};
q[++cnt]=(node){l1-1,l2-1,i,1};
}
for(int i=1;i<=cnt;i++) if(q[i].l>q[i].r) swap(q[i].l,q[i].r);
sort(q+1,q+cnt+1);l=r=0;
for(int i=1;i<=cnt;i++){
while(r<q[i].r) mr(1);
while(r>q[i].r) mr(-1);
while(l<q[i].l) ml(1);
while(l>q[i].l) ml(-1);
ans[q[i].id]+=1ll*q[i].op*res;
}
for(int i=1;i<=m;i++) cout<<ans[i]<<'\n';
return 0;
}
P4689 差分好题 - 莫队基础
给一个树,\(n\) 个点,有点权,初始根是 \(1\)。
\(m\) 个操作,每次操作:
- 将树根换为 \(x\)
- 给出两个点 \(x,y\),从 \(x\) 的子树中选每一个点,\(y\) 的子树中选每一个点,如果两个点点权相等,\(ans++\),求 \(ans\)
\(1 \le n \le 10^5,1 \le m \le 5 \times 10^5\)。
首先换根是假的。
可以直接在 dfs 序上面变成区间查询或者区间的补集。
于是我们再对询问进行一个差分,和上面那道题类似去维护即可。
注意 dep 的减法不要写反了!
Code
#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define pb push_back
#define pii pair<int,int>
#define fi first
#define se second
const int N=1e5+5,M=2e6+5;
int n,m,a[N],col[N],dfn[N],idx=0,sz[N],dep[N],f[N][19],cl[N],cr[N],l,r,B,cnt=0,tim=0,b[N],rt;
ll ans[M],cur;
struct node{
int l,r,id,op;
bool operator <(const node &rhs) const{
if((l/B)!=(rhs.l/B)) return (l/B)<(rhs.l/B);
return r<rhs.r;
}
}q[M];
struct edge{int v,nxt;}e[N<<1];
int head[N],tot=0;
void add(int u,int v){
e[++tot]=(edge){v,head[u]};head[u]=tot;
e[++tot]=(edge){u,head[v]};head[v]=tot;
}
void dfs(int u,int fa){
dep[u]=dep[fa]+1;dfn[u]=++idx;sz[u]=1;
f[u][0]=fa;
for(int i=1;f[f[u][i-1]][i-1];++i) f[u][i]=f[f[u][i-1]][i-1];
for(int i=head[u];i;i=e[i].nxt){
int v=e[i].v;
if(v==fa) continue;
dfs(v,u);sz[u]+=sz[v];
}
}
int getk(int x,int k){
for(int i=17;i>=0;i--) if(k>=(1<<i)) k-=(1<<i),x=f[x][i];
return x;
}
void ins(int l1,int r1,int l2,int r2,int t){
q[++cnt]=(node){l1-1,l2-1,t,1};
q[++cnt]=(node){r1,r2,t,1};
q[++cnt]=(node){r1,l2-1,t,-1};
q[++cnt]=(node){l1-1,r2,t,-1};
}
vector<pii> calc(int x){
vector<pii> res;res.resize(0);
if(x==rt){res.pb({1,n});return res;}
if(dfn[x]<=dfn[rt]&&dfn[x]+sz[x]-1>=dfn[rt]){
int u=getk(rt,dep[rt]-dep[x]-1);
if(dfn[u]-1>=1) res.pb({1,dfn[u]-1});
if(dfn[u]+sz[u]<=n) res.pb({dfn[u]+sz[u],n});
}
else res.pb({dfn[x],dfn[x]+sz[x]-1});
return res;
}
void ml(int x){
if(x==1) ++l,++cl[col[l]],cur+=cr[col[l]];
else --cl[col[l]],cur-=cr[col[l]],--l;
}
void mr(int x){
if(x==1) ++r,++cr[col[r]],cur+=cl[col[r]];
else --cr[col[r]],cur-=cl[col[r]],--r;
}
int main(){
/*2023.12.6 H_W_Y P4689 [Ynoi2016] 这是我自己的发明 md*/
ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
cin>>n>>m;rt=1;
for(int i=1;i<=n;i++) cin>>a[i],b[i]=a[i];
sort(b+1,b+n+1);int len=unique(b+1,b+n+1)-b-1;
for(int i=1,u,v;i<n;i++) cin>>u>>v,add(u,v);
dfs(1,0);
for(int i=1;i<=n;i++) col[dfn[i]]=lower_bound(b+1,b+len+1,a[i])-b;
for(int i=1,op,x,y;i<=m;i++){
cin>>op;
if(op==1) cin>>rt;
else{
cin>>x>>y;++tim;
vector<pii> px,py;
px=calc(x);py=calc(y);
for(auto j:px) for(auto k:py) ins(j.fi,j.se,k.fi,k.se,tim);
}
}
B=sqrt(n);
for(int i=1;i<=cnt;i++) if(q[i].l>q[i].r) swap(q[i].l,q[i].r);
sort(q+1,q+cnt+1);l=r=1;cur=0;
for(int i=1;i<=cnt;i++){
while(r<q[i].r) mr(1);
while(r>q[i].r) mr(-1);
while(l<q[i].l) ml(1);
while(l>q[i].l) ml(-1);
ans[q[i].id]+=1ll*q[i].op*cur;
}
for(int i=1;i<=tim;i++) cout<<ans[i]<<'\n';
return 0;
}
P3245 大数 - 差分 + 莫队基础 + 区间子区间
给一个数字串以及一个质数 \(p\)。
多次查询这个数字串的一个子串里有多少个子串是 \(p\) 的倍数。
\(1 \le n,m \le 2 \times 10^5\)。
一道让我印象非常深刻的题目。
还是先考虑差分,
但是发现前缀做差分是很难做的,因为不同的区间长度会带来乘上不同的 \(10^i\)。
所以我们考虑对于后缀做差分。
一个区间 \([l,r]\) 满足条件当且仅当 \(suf[r+1] \equiv suf[l] \pmod p\),
于是我们直接维护就好了。
离散化之后就变成小 Z 的袜子了。
而要注意我们需要对 \(p=2,5\) 进行特判,而这也是好处理的,
直接判断奇偶或者 \(0,5\) 即可。
Code
#include <bits/stdc++.h>
using namespace std;
#define ll long long
const int N=2e5+5;
int n,m,a[N],b[N],B,c[N],l,r;
ll p,ans[N],res=0,nw=1ll;
string s;
struct node{
int l,r,id;
bool operator <(const node &rhs) const{
if((l/B)!=(rhs.l/B)) return (l/B)<(rhs.l/B);
return r<rhs.r;
}
}q[N];
void ins(int x){res+=c[x];++c[x];}
void del(int x){--c[x];res-=c[x];}
bool chk(ll p,char ch){
if(p==2&&(ch-'0')%2==0) return true;
if(p==5&&(ch-'0')%5==0) return true;
return false;
}
void sol(){
n=s.size();
for(int i=0;i<n;i++) if(chk(p,s[i])) ++c[i+1],ans[i+1]=1ll*(i+1);
for(int i=1;i<=n;i++) c[i]+=c[i-1],ans[i]+=ans[i-1];
cin>>m;
for(int i=1;i<=m;i++){
cin>>l>>r;
cout<<(ans[r]-ans[l-1]-1ll*(c[r]-c[l-1])*(l-1))<<'\n';
}
}
int main(){
/*2023.12.5 H_W_Y P3245 [HNOI2016] 大数 md*/
ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
cin>>p>>s;
if(p==2||p==5) sol(),exit(0);
n=s.size();B=sqrt(n);nw=1ll;
for(int i=n-1;i>=0;i--) a[i+1]=(1ll*a[i+2]+1ll*nw*(s[i]-'0')%p)%p,nw=10ll*nw%p;
++n;
for(int i=1;i<=n;i++) b[i]=a[i];
sort(b+1,b+n+1);
for(int i=1;i<=n;i++) a[i]=lower_bound(b+1,b+n+1,a[i])-b;
cin>>m;
for(int i=1;i<=m;i++) cin>>q[i].l>>q[i].r,++q[i].r,q[i].id=i;
sort(q+1,q+m+1);l=1,r=0;
for(int i=1;i<=m;i++){
while(r<q[i].r) ins(a[++r]);
while(l>q[i].l) ins(a[--l]);
while(r>q[i].r) del(a[r--]);
while(l<q[i].l) del(a[l++]);
ans[q[i].id]=res;
}
for(int i=1;i<=m;i++) cout<<ans[i]<<'\n';
return 0;
}
P3604 美好的每一天 - 莫队基础 + 区间子区间
给一个小写字母的字符串。
每次查询区间有多少子区间可以重排成为一个回文串。
\(n,m \le 6 \times 10^4\)。
同样发现一个区间满足条件当且仅当只有最多一种字符出现了奇数次,
于是我们不难想到可以异或完成。
把这 \(26\) 个字符分别变成 \(2^i\),
于是满足条件就变成了区间的异或和为 \(0,2^0,2^1,\dots,2^{25}\)。
这样同样就变成了一个简单的问题,
每次加入一个元素的时候我们枚举一下 \(26\) 种合法的值就可以了。
Code
#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define pb push_back
const int N=1e5+5;
int n,m,a[N],p[27],B,l,r,c[N],b[N],len;
ll ans[N],res=0;
map<int,int> mp;
vector<int> g[N];
char ch;
struct node{
int l,r,id;
bool operator <(const node &rhs) const{
if((l/B)!=(rhs.l/B)) return (l/B)<(rhs.l/B);
return r<rhs.r;
}
}q[N];
void init(){p[0]=1;for(int i=1;i<26;i++) p[i]=2*p[i-1];p[26]=0;}
void ins(int x){for(auto i:g[x]) res+=1ll*c[i];++c[x];}
void del(int x){--c[x];for(auto i:g[x]) res-=1ll*c[i];}
int main(){
/*2023.12.5 H_W_Y P3604 美好的每一天 md*/
ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
cin>>n>>m;init();B=sqrt(n);
memset(c,0,sizeof(c));
for(int i=1;i<=n;i++){
cin>>ch;
while(!(ch>='a'&&ch<='z')) cin>>ch;
a[i]=a[i-1]^p[ch-'a'];b[i]=a[i];
}
b[++n]=0;
sort(b+1,b+n+1);len=unique(b+1,b+n+1)-b-1;
for(int i=0;i<=n;i++) a[i]=lower_bound(b+1,b+len+1,a[i])-b;
for(int i=1;i<=len;i++) mp[b[i]]=i;
for(int i=1;i<=len;i++){
for(int j=0;j<=26;j++) if(mp.count(b[i]^p[j])) g[i].pb(mp[b[i]^p[j]]);
}
for(int i=1;i<=m;i++) cin>>q[i].l>>q[i].r,--q[i].l,q[i].id=i;
sort(q+1,q+m+1);l=0,r=-1;
for(int i=1;i<=m;i++){
while(r<q[i].r) ins(a[++r]);
while(l>q[i].l) ins(a[--l]);
while(r>q[i].r) del(a[r--]);
while(l<q[i].l) del(a[l++]);
ans[q[i].id]=res;
}
for(int i=1;i<=m;i++) cout<<ans[i]<<'\n';
return 0;
}
P5906 - 回滚莫队
给定一个序列,多次询问一段区间 \([l,r]\),求区间中相同的数的最远间隔距离。
序列中两个元素的间隔距离指的是两个元素下标差的绝对值。
\(1\leq n,m\leq 2\cdot 10^5\),\(1\leq a_i\leq 2\cdot 10^9\)。
回滚莫队的板子。
发现删除操作是不好做的,
于是我们用栈维护一下,把删除改成撤销去维护即可。
Code
#include <bits/stdc++.h>
using namespace std;
int read(){
int x=0,f=1;char ch=getchar();
while(!isdigit(ch)){if(ch=='-') f=-1;ch=getchar();}
while(isdigit(ch)){x=(x<<1)+(x<<3)+ch-'0';ch=getchar();}
return x*f;
}
void print(int x){
int p[15],tmp=0;
if(x==0) putchar('0');
if(x<0) putchar('-'),x=-x;
while(x) p[++tmp]=x%10,x/=10;
for(int i=tmp;i>=1;--i) putchar(p[i]+'0');
putchar('\n');
}
inline int max(const int &x,const int &y){return x>y?x:y;}
const int N=2e5+5;
int n,m,a[N],b[N],lst[N],ans[N],num=0,bl[N],B,len,st[N],del[N],ct=0;
struct node{
int l,r,id;
bool operator <(const node &rhs) const{
if(bl[l]!=bl[rhs.l]) return bl[l]<bl[rhs.l];
return r<rhs.r;
}
}q[N];
int calc(int l,int r){
int res=0;
for(int i=l;i<=r;++i) (!lst[a[i]])?lst[a[i]]=i:res=max(res,i-lst[a[i]]);
for(int i=l;i<=r;++i) lst[a[i]]=0;
return res;
}
int main(){
/*2023.12.5 H_W_Y P5906 【模板】回滚莫队&不删除莫队 md*/
n=read();B=sqrt(n);
for(int i=1;i<=n;++i) a[i]=read(),b[i]=a[i],bl[i]=(i-1)/B+1;
sort(b+1,b+n+1);len=unique(b+1,b+n+1)-b-1;num=bl[n];
for(int i=1;i<=n;++i) a[i]=lower_bound(b+1,b+len+1,a[i])-b;
m=read();
for(int i=1;i<=m;++i) q[i].l=read(),q[i].r=read(),q[i].id=i;
sort(q+1,q+m+1);
for(int i=1,j=1;j<=num;++j){
int br=min(n,j*B),l=br+1,r=br,res=0;ct=0;
for(;i<=m&&bl[q[i].l]==j;++i){
if(bl[q[i].r]==j){ans[q[i].id]=calc(q[i].l,q[i].r);continue;}
while(r<q[i].r){
++r;lst[a[r]]=r;
if(!st[a[r]]) st[a[r]]=r,del[++ct]=a[r];
res=max(res,r-st[a[r]]);
}
int cur=res;
while(l>q[i].l){
--l;
if(!lst[a[l]]) lst[a[l]]=l;
res=max(res,lst[a[l]]-l);
}
ans[q[i].id]=res;
while(l<=br){
if(lst[a[l]]==l) lst[a[l]]=0;
l++;
}
res=cur;
}
while(ct) lst[del[ct]]=st[del[ct]]=0,--ct;
}
for(int i=1;i<=m;i++) print(ans[i]);
return 0;
}
把 \(num\) 赋值成 \(b[n]\),虚空调试半个小时。
BZOJ 4358 premu - 回滚莫队
给一个长为 \(n\) 的排列。
有 \(m\) 次查询,每次查询给出 \([l,r]\),输出最大的 \((j-i)\) 满足:
\(i,i+1,\dots, j\) 这些值都在区间 \([l,r]\) 中出现过。
\(1 \le n,q \le 2 \times 10^5\)。
我们用 \(01\) 去维护值域,
\(1\) 表示出现过的,于是我们只需要维护每一个 \(1\) 的段的左端点和右端点,左端点指向右端点,右端点指向左端点,
加入一个节点时直接 \(\mathcal O(1)\) 修改,用链表维护序列即可。
而由于我们需要取最大值,是不支持删除的,
所以用回滚莫队完成即可。
想是好想的,但是发现实现好难?!
可是一看代码?!怎么这么断,可能是对回滚莫队有一些无解吧。
具体实现中,我们用 \(u,d\) 两个数组分别记录第 \(i\) 个点往左往右能走到的地方即可。
Code
#include <bits/stdc++.h>
using namespace std;
#define pii pair<int,int>
#define fi first
#define se second
const int N=2e5+5;
int n,a[N],u[N],d[N],B,m,tp=0,ans[N],res=0,cur=0,bl[N];
struct node{
int l,r,id;
bool operator <(const node &rhs) const{
if(bl[l]!=bl[rhs.l]) return bl[l]<bl[rhs.l];
return r<rhs.r;
}
}q[N];
pii s[N];
void ins(int x){
u[x]=u[x+1]+1;d[x]=d[x-1]+1;
int len=u[x]+d[x]-1;
s[++tp]={x+u[x]-1,d[x+u[x]-1]};
s[++tp]={x-d[x]+1,u[x-d[x]+1]};
d[x+u[x]-1]=u[x-d[x]+1]=len;
res=max(res,len);
}
int main(){
/*2023.12.6 H_W_Y bzoj4358 permu md*/
ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
cin>>n>>m;B=sqrt(n);
for(int i=1;i<=n;i++) cin>>a[i],bl[i]=(i-1)/B+1;
for(int i=1;i<=m;i++) cin>>q[i].l>>q[i].r,q[i].id=i;
sort(q+1,q+m+1);
for(int i=1,r=0,br=0;i<=m;i++){
if(bl[q[i].l]!=bl[q[i-1].l]){
for(int j=0;j<=n;j++) u[j]=d[j]=0;
cur=res=0;r=br=B*bl[q[i].l];
}
res=tp=0;
while(r<q[i].r) ins(a[++r]);
tp=0;cur=res=max(cur,res);
for(int j=q[i].l;j<=min(q[i].r,br);j++) ins(a[j]);
ans[q[i].id]=res;
for(int j=tp;j>=1;j--) (j&1)?d[s[j].fi]=s[j].se:u[s[j].fi]=s[j].se;
for(int j=q[i].l;j<=min(q[i].r,br);j++) u[a[j]]=d[a[j]]=0;
}
for(int i=1;i<=m;i++) cout<<ans[i]<<'\n';
return 0;
}
P5386 [Cnoi2019] 数字游戏 - 回滚莫队(对值域)+ 区间子区间
给定一个排列,多次询问,求一个区间 \([l,r]\) 有多少个子区间的值都在区间 \([x,y]\) 内。
\(1 \le n,q \le 2 \times 10^5\)。
我们对值域莫队,而用上一题类似的方法即可得到一个 \(01\) 串,
于是我们需要维护的就是最长的全 \(1\) 段的平方和。
这个东西我们可以对它进行分块,直接维护即可。
没看题解代码打出来了(虽然时间有点长。)
Code
#include <bits/stdc++.h>
using namespace std;
#define ll long long
const int N=5e5+5;
int n,m,pos[N],bl[N],B,Bq,L[N],R[N],num,tp,tpn=0,u[N],d[N];
ll ans[N];
struct query{
int l,r,id,a,b;
bool operator <(const query &rhs)const{
if(((l-1)/Bq)!=((rhs.l-1)/Bq)) return ((l-1)/Bq)<((rhs.l-1)/Bq);
return r<rhs.r;
}
}q[N];
struct node{ll ans;int l,r;bool vis;}t[N];
struct stk{int op,id,val;}s[N];
struct stn{int id;node val;}st[N];
ll sq(int x){return 1ll*x*(x+1)/2ll;}
node merge(node a,node b){
node res;res.vis=false;
if(a.vis&&b.vis) return (node){0,a.l+b.l,a.r+b.r,1};
if(a.vis) res.l=a.l+b.l,res.r=b.r,res.ans=b.ans;
else if(b.vis) res.l=a.l,res.r=b.r+a.r,res.ans=a.ans;
else res.l=a.l,res.r=b.r,res.ans=a.ans+b.ans+sq(a.r+b.l);
return res;
}
void ins(int x){
int nw=bl[x],len=0;
st[++tpn]=(stn){nw,t[nw]};
if(x==L[nw]){
d[x]=1;u[x]=len=u[x+1]+1;
s[++tp]=(stk){1,u[x]+x-1,d[u[x]+x-1]};
if(len==R[nw]-L[nw]+1) t[nw].l=t[nw].r=len,t[nw].vis=true,t[nw].ans=0;
else t[nw].ans-=sq(u[x+1]),t[nw].l=len;
d[u[x]+x-1]=len;
}
else if(x==R[nw]){
d[x]=len=d[x-1]+1,u[x]=1;
s[++tp]=(stk){0,x-d[x]+1,u[x-d[x]+1]};
if(len==R[nw]-L[nw]+1) t[nw].l=t[nw].r=len,t[nw].vis=true,t[nw].ans=0;
else t[nw].ans-=sq(d[x-1]),t[nw].r=len;
u[x-d[x]+1]=len;
}
else{
d[x]=d[x-1]+1,u[x]=u[x+1]+1;len=u[x]+d[x]-1;
s[++tp]=(stk){0,x-d[x]+1,u[x-d[x]+1]};
s[++tp]=(stk){1,x+u[x]-1,d[x+u[x]-1]};
if(len==R[nw]-L[nw]+1) t[nw].l=t[nw].r=len,t[nw].vis=true,t[nw].ans=0;
else if(x-d[x]+1==L[nw]) t[nw].ans-=sq(u[x+1]),t[nw].l=len;
else if(x+u[x]-1==R[nw]) t[nw].ans-=sq(d[x-1]),t[nw].r=len;
else t[nw].ans+=sq(len)-sq(d[x-1])-sq(u[x+1]);
d[x+u[x]-1]=u[x-d[x]+1]=len;
}
}
node g(int l,int r){
int lf=0,rf=0,lst=0;
node res;res.ans=res.vis=0;
for(int i=r;i>=l;i--) if(!u[i]){rf=i,res.r=r-i;break;}
if(!rf) return (node){0,r-l+1,r-l+1,1};
for(int i=l;i<=r;i++) if(!u[i]){lf=i,res.l=i-l;break;}
for(int i=lf;i<=rf;i++){
if(u[i]&&!lst) lst=i;
if(!u[i]&&lst) res.ans+=sq(i-lst),lst=0;
}
return res;
}
ll qry(int l,int r){
if(bl[l]==bl[r]){
node res=g(l,r);
if(res.vis) return sq(res.l);
return res.ans+sq(res.l)+sq(res.r);
}
node res=g(l,R[bl[l]]);
for(int i=bl[l]+1;i<bl[r];i++) res=merge(res,t[i]);
res=merge(res,g(L[bl[r]],r));
if(res.vis) return sq(res.l);
return res.ans+sq(res.l)+sq(res.r);
}
int find(int i){return (i-1)/Bq+1;}
int main(){
/*2023.12.6 H_W_Y P5386 [Cnoi2019] 数字游戏 回滚莫队*/
ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
cin>>n>>m;Bq=(int)1.0*n/sqrt(m);B=sqrt(n);num=(n-1)/B+1;
for(int i=1,x;i<=n;i++) cin>>x,pos[x]=i,bl[i]=(i-1)/B+1;
for(int i=1;i<=num;i++) L[i]=R[i-1]+1,R[i]=min(L[i]+B-1,n);
for(int i=1;i<=m;i++) cin>>q[i].a>>q[i].b>>q[i].l>>q[i].r,q[i].id=i;
sort(q+1,q+m+1);
for(int i=1,br=0,r=0;i<=m;i++){
if(i==1||find(q[i].l)!=find(q[i-1].l)){
for(int j=0;j<=n;j++) u[j]=d[j]=0;
for(int j=0;j<=num;j++) t[j].l=t[j].r=t[j].ans=t[j].vis=0;
r=br=find(q[i].l)*Bq;
}
tp=tpn=0;
while(r<q[i].r) ins(pos[++r]);
tp=tpn=0;
for(int j=q[i].l;j<=min(q[i].r,br);j++) ins(pos[j]);
ans[q[i].id]=qry(q[i].a,q[i].b);
for(int j=tp;j>=1;j--) (s[j].op)?d[s[j].id]=s[j].val:u[s[j].id]=s[j].val;
for(int j=tpn;j>=1;j--) t[st[j].id]=st[j].val;
for(int j=q[i].l;j<=min(q[i].r,br);j++) u[pos[j]]=d[pos[j]]=0;
}
for(int i=1;i<=m;i++) cout<<ans[i]<<'\n';
return 0;
}
感觉比 Day 1 的好调多了。
P5901 [IOI2009] Regions - 根号分治
\(N\) 个节点的树,有 \(R\) 种属性,每个点属于一种属性。
有 \(Q\) 次询问,每次询问 \(r1,r2\),回答有多少对 \((e1,e2)\) 满足 \(e1\) 属性是 \(r1\),\(e2\) 属性是 \(r2\),\(e1\) 是 \(e2\) 的祖先。
\(1 \le N,Q \le 2 \times 10^5\)。
将询问离线下来
直接对属性进行根号分治即可。
具体来说,对于个数 \(\ge \sqrt n\) 的属性我们提前预处理出来它与其他属性的答案。
而对于其他的,我们直接用双指针跑就可以了。
双指针可以优化掉一个 \(\log\)!!!
Code
#include <bits/stdc++.h>
using namespace std;
#define pb push_back
const int N=1e6+5;
int n,m,q,a[N],sz[N],dfn[N],ed[N],lim,idx=0,s[N],head[N],tot=0;
vector<int> g[N],rev[N],lg,ans[2][N];
bool vis[N];
struct edge{
int v,nxt;
}e[N<<1];
void add(int u,int v){e[++tot]=(edge){v,head[u]};head[u]=tot;}
void dfs(int u){
dfn[u]=++idx;
for(int i=head[u];i;i=e[i].nxt) dfs(e[i].v);
ed[u]=idx;
}
void dfs1(int u){for(int i=head[u];i;i=e[i].nxt) dfs1(e[i].v),s[u]+=s[e[i].v];}
void dfs2(int u){for(int i=head[u];i;i=e[i].nxt) s[e[i].v]+=s[u],dfs2(e[i].v);}
bool cmp1(int x,int y){return dfn[x]<dfn[y];}
bool cmp2(int x,int y){return ed[x]<ed[y];}
void init(){for(int i=0;i<=n;i++) s[i]=0;}
int main(){
/*2023.12.6 H_W_Y P5901 [IOI2009] Regions ghfz*/
ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
cin>>n>>m>>q>>a[1];lim=sqrt(n);sz[a[1]]++;g[a[1]].pb(1);
for(int i=2,x;i<=n;i++) cin>>x>>a[i],add(x,i),g[a[i]].pb(i),sz[a[i]]++;
dfs(1);
for(int i=1;i<=m;i++){
if(sz[i]>=lim) lg.pb(i),vis[i]=true;
sort(g[i].begin(),g[i].end(),cmp1),rev[i]=g[i],sort(rev[i].begin(),rev[i].end(),cmp2);
}
for(int i=0;i<(int)lg.size();i++){
int nw=lg[i];
ans[0][nw].resize(m+1);ans[1][nw].resize(m+1);
init();for(auto j:g[nw]) ++s[j];dfs1(1);
for(int j=1;j<=n;j++) ans[0][nw][a[j]]+=s[j];
init();for(auto j:g[nw]) ++s[j];dfs2(1);
for(int j=1;j<=n;j++) ans[1][nw][a[j]]+=s[j];
}
while(q--){
int x,y;cin>>x>>y;
if(vis[x]) cout<<ans[1][x][y]<<endl;
else if(vis[y]) cout<<ans[0][y][x]<<endl;
else{
int cur=sz[x]*sz[y];
for(int i=0,j=-1;i<(int)g[x].size();i++){
while(j+1<(int)g[y].size()&&dfn[g[y][j+1]]<dfn[g[x][i]]) ++j;
cur-=j+1;
}
for(int i=(int)g[x].size()-1,j=(int)g[y].size();i>=0;i--){
while(j-1>=0&&dfn[g[y][j-1]]>ed[rev[x][i]]) --j;
cur-=(int)g[y].size()-j;
}
cout<<cur<<endl;
}
}
return 0;
}
P9809 Homework - 根号分治
1 X: 在集合 \(S\) 中加入一个X,保证 X 在当前集合中不存在。
2 Y: 在当前的集合中询问所有 \(X \mod Y\) 最小的值
\(X,Y \le 10^5\)。
很明显直接对 \(Y\) 根号分治即可。
而对于 \(Y\) 较大的,我们对值域分块,最多只会有 \(\sqrt n\) 个块,
具体实现时直接用 set 维护一下即可。
Code
#include <bits/stdc++.h>
using namespace std;
const int N=1e5+5,inf=0x3f3f3f3f;
int n,a[N],x;
set<int> s;
int main(){
/*2023.12.5 H_W_Y P9809 [SHOI2006] 作业 Homework 根号分治*/
ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
cin>>n;memset(a,0x3f,sizeof(a));
for(int i=1;i<=n;i++){
char ch;cin>>ch;
while(ch!='A'&&ch!='B') cin>>ch;
cin>>x;
if(ch=='A'){s.insert(x);for(int j=1;j<549;j++) a[j]=min(a[j],x%j);}
else{
if(x<549) cout<<a[x]<<'\n';
else{
int nw=x,ans;auto it=s.lower_bound(0);
ans=(*it)%x;
while((it=s.lower_bound(nw))!=s.end())
ans=min(ans,(*it)%x),nw+=x;
cout<<ans<<'\n';
}
}
}
return 0;
}
P9060 Ynoi2002 - 根号分治 + 区间子区间
P9060 [Ynoi2002] Goedel Machine
给定一个长度为 \(n\) 的序列 \(a_1\cdots a_n\)。你需要回答 \(m\) 个询问,第 \(i\) 个询问给定一个区间 \([l_i,r_i]\),请你求出这个区间中所有非空子集的最大公约数的乘积。
由于答案可能很大,每次询问请你求出其对 \(998244353\) 取模的结果。
\(1 \le n,m,a_i \le 10^5\)。
居然是 2023.8.5 的联考题,不愧是 CQYC 的。
当时记得在机场看的这道题,才办完托运,感觉真的根本不可做——那一场都不可做吧。
后面到了 London 看了后面一道题的题解就没有管这道题了。
看到区间子区间就不知道怎么下手了。
感觉可以用单调栈,对于每一个质数拆开算贡献,然后再用一个扫描线维护一下,
也就是扫描线的区间子区间问题,
而对于大的质数我们直接暴力?
可能还真可以,只不过常数比较大,可能写着也比较复杂。
考虑正常的做法。
首先按每一个质数分别算贡献是没有问题的,
那么如果这个质数再 \(x\) 个数中都出现了,那么它的贡献是 \(p^{2^x-1}\),这是好理解的。
但是现在发现了一个严重的问题——\(p\) 还有很多的幂,这是不好统计的。
于是我们考虑根号分治,按照 \(\sqrt w\) 分成两部分。
对于 \(\le \sqrt w\) 的部分,有大概 \(\frac{\sqrt n}{\log n}\) 个质数,于是加上它们的幂就有 \(\sqrt n\) 个数。
于是我们对这 \(\sqrt n\) 个数分别算出在每一个数中的出现次数,加上它们的贡献即可,这是可以提前预处理得到的。
对于 \(\gt \sqrt w\) 的部分,每一个数只会出现一次,就是说幂是 \(1\) 的。
所以我们直接用莫队维护一下出现次数即可。
代码中用到了算 \(2^k-1\) 的技巧,就每一次加上 \(2^i\) 就可以了。
注意空间问题,有可能会越界(\(t\) 数组),所以循环的时候只能枚举到 \(\lt s[i]\)。
Code
#include <bits/stdc++.h>
using namespace std;
#define ll long long
const ll mod=998244353;
const int N=1e5+5;
int lim,n,m,a[N],p[N],cnt=0,s[N],mx,B,len=0,c[N],t[N],l,r,pos[N];
ll ans[N],res_pos,res_inv;
bool vis[N];
struct node{
int l,r,id;
bool operator <(const node &rhs) const{
if((l/B)!=(rhs.l/B)) return (l/B)<(rhs.l/B);
return r<rhs.r;
}
}q[N];
ll qpow(ll a,ll b){
ll res=1ll;
while(b){if(b&1) res=res*a%mod;a=a*a%mod;b>>=1;}
return res;
}
void init(int lim){
for(int i=2;i<=lim;++i){
if(!vis[i]) p[++cnt]=i;
for(int j=1;j<=cnt&&p[j]*i<=lim;++j){
vis[p[j]*i]=true;
if(i%p[j]==0) break;
}
}
}
void ins(int x){if(x>1) res_pos=1ll*res_pos*t[pos[x]+(c[x]++)]%mod;}
void del(int x){if(x>1) res_inv=1ll*res_inv*t[pos[x]+(--c[x])]%mod;}
int main(){
/*2023.12.5 H_W_Y P9060 [Ynoi2002] Goedel Machine md*/
ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
cin>>n>>m;B=n/sqrt(m);
for(int i=1;i<=n;++i) cin>>a[i],mx=max(mx,a[i]);
init((lim=sqrt(mx)));
for(int i=1;i<=m;i++) cin>>q[i].l>>q[i].r,q[i].id=i,ans[i]=1ll;
for(int k=1;k<=cnt;k++){
int nw=1ll*p[k],inv=(int)qpow(nw,mod-2);t[0]=nw;
for(int i=1;i<=n;++i) t[i]=1ll*t[i-1]*t[i-1]%mod;
for(int j=nw;j<=mx;j*=nw){
for(int i=1;i<=n;i++) s[i]=s[i-1]+(a[i]%j==0);
for(int i=1;i<=m;i++) ans[i]=1ll*ans[i]*t[s[q[i].r]-s[q[i].l-1]]%mod*inv%mod;
}
for(int i=1;i<=n;i++) while(a[i]%nw==0) a[i]/=nw;
}
memset(s,0,sizeof(s));cnt=0;
for(int i=1;i<=n;i++) if(a[i]>1) s[a[i]]++;
for(int i=1;i<=mx;i++) if(s[i]){
t[pos[i]=++cnt]=i;
for(int j=1;j<s[i];j++) ++cnt,t[cnt]=1ll*t[cnt-1]*t[cnt-1]%mod;
}
memset(c,0,sizeof(c));
sort(q+1,q+m+1);l=1,r=0;res_pos=res_inv=1ll;
for(int i=1;i<=m;i++){
while(r<q[i].r) ins(a[++r]);
while(l>q[i].l) ins(a[--l]);
while(r>q[i].r) del(a[r--]);
while(l<q[i].l) del(a[l++]);
ans[q[i].id]=1ll*ans[q[i].id]*res_pos%mod*qpow(res_inv,mod-2)%mod;
}
for(int i=1;i<=m;i++) cout<<ans[i]<<'\n';
return 0;
}
Conclusion
- 有关质因子一般都是根号分治之后,小的暴力预处理,大的用莫队维护。
- 一定要注意值域的范围,从而很有可能出现越界情况。(很多题)
- 双指针很多时候可以优化掉一个 \(\log\),可以常往这方面思考。(P5901 [IOI2009] Regions)
- 回滚莫队撤销的时候一定要倒序撤销!(BZOJ4358 permu)
2023.12.6 21:04 补完。
Day 4 分块 + 树套树 + cdq 分治
20231205
主要是一些分块的技巧和树套树。
根号分治+莫队:P5071,P9060
分块:P6779,P7446,P5063
树套树:P3810,P4054,P3157,P3759,P3332,P9068,P4690,LOJ6120
树套树标记永久化:P3242,BZOJ3489
Keynote
分块 的技巧。
分块希望完成的:快速整块修改 和 快速零散块重构。
- 一个数本质不同的质因子个数是 \(O(\frac{\log V}{\log \log V})\)。
- 分块很多时候都可以用均摊的思路,我们可以把每一个块拿出来单独处理。
cdq 分治和树套树主要是解决 单点修改,矩形求和 的问题。
cdq:时间常数小,空间复杂度低,离线
STS:在线(不能下放标记)
做题时还是要首先考虑差分,
能差分就可以直接用树状数组维护,这样会大大减少代码量。
所以树套树最常见的就是 树状数组 + 平衡树。
对于 升维,降维,有以下几种方法:
升维:
- 区间中颜色数 \(\to \mathcal O(\log n)\)。
- 区间中值在一个区间 \(\to \mathcal O(\log^2n)\)。
- 区间颜色数带修 \(\to\) 多了时间轴。
降维:
- 差分
- 容斥(总的减去不满足条件的)
\(n=1e5,m=1e6\) 的数据范围:
- 用根号数据结构做到 \(\mathcal O(n \sqrt m)\)。
- 用 polylog 的做法,一般 \(\mathcal O(n \log ^2n+m\log n)\)。
P5071 Ynoi2015 - 根号分治
珂朵莉给你了一个长为 \(n\) 的序列,有 \(m\) 次查询,每次查询一段区间的乘积的约数个数 \(\mod 19260817\) 的值。
\(1 \le n,m \le 10^5,v \le 10^9\)。
很容易发现我们只需要把每一个数进行质因数分解,
因数个数就是 \((c_1+1)(c_2+1) \dots\)(小学奥数知识)。
这样直接用分块维护,复杂度时带 \(\log\) 的,
在这道题中根本过不了。
所以我们需要考虑一种新的方法。
发现对于每一个数 \(\ge 1000\) 的质数只有可以有两个,
于是我们对于 \(\lt 1000\) 的 \(168\) 个质数进行暴力的维护,而只对那两个大质数在莫队时维护即可。
具体实现的时候就需要先把 \(\lt 1000\) 的质数做一个前缀和即可。
Code
#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define pb push_back
const ll mod=19260817;
const int N=1e5+5,M=1e6+5;
int n,m,x,s[N][169],c[M],cnt=0,p[M],bl[N],B,l,r,len=0;
vector<int> g[N];
ll inv[M],ans[M],res=0;
struct node{
int l,r,id;
bool operator <(const node &rhs) const{
if(bl[l]!=bl[rhs.l]) return bl[l]<bl[rhs.l];
return r<rhs.r;
}
}q[M];
bool vis[M];
void init(){
inv[1]=1;
for(int i=2;i<M;i++) inv[i]=inv[mod%i]*(mod-mod/(1ll*i))%mod;
for(int i=2;i<M;i++){
if(!vis[i]) p[++cnt]=i;
for(int j=1;j<=cnt&&p[j]*i<M;j++){
vis[p[j]*i]=true;
if(i%p[j]==0) break;
}
}
}
void chg(int i,int v){
for(auto j:g[i]){
res=res*inv[c[j]+1]%mod;
c[j]+=v;
res=1ll*res*(c[j]+1ll)%mod;
}
}
int main(){
/*2023.12.5 H_W_Y P5071 [Ynoi2015] 此时此刻的光辉 md*/
ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
init();
cin>>n>>m;B=(int)floor(sqrt(n));
for(int i=1;i<=n;i++){
cin>>x;bl[i]=(i-1)/B+1;
for(int j=1;j<=168;j++)
while(x%p[j]==0) s[i][j]++,x/=p[j];
for(int j=169;j<=cnt&&p[j]*p[j]<=x;j++)
if(x%p[j]==0){
g[i].pb(p[j]),x/=p[j];
c[++len]=p[j];
break;
}
if(x!=1) g[i].pb(x),c[++len]=x;
}
sort(c+1,c+len+1);
len=unique(c+1,c+len+1)-c-1;
for(int i=1;i<=n;i++){
for(int j=0;j<(int)g[i].size();j++)
g[i][j]=lower_bound(c+1,c+len+1,g[i][j])-c;
for(int j=1;j<=168;j++)
s[i][j]+=s[i-1][j];
}
memset(c,0,sizeof(c));
for(int i=1;i<=m;i++){
cin>>q[i].l>>q[i].r;
ans[i]=1ll;q[i].id=i;
for(int j=1;j<=168;j++)
ans[i]=1ll*ans[i]*(s[q[i].r][j]-s[q[i].l-1][j]+1ll)%mod;
}
sort(q+1,q+m+1);
l=1;r=0;res=1ll;
for(int i=1;i<=m;i++){
while(r<q[i].r) chg(++r,1);
while(l>q[i].l) chg(--l,1);
while(r>q[i].r) chg(r--,-1);
while(l<q[i].l) chg(l++,-1);
(ans[q[i].id]*=res)%=mod;
}
for(int i=1;i<=m;i++) cout<<ans[i]<<'\n';
return 0;
}
P6779 Ynoi2009 - 分块逐块处理 + 均摊
给定一棵 \(n\) 个节点的树,树有边权,与一个长为 \(n\) 的序列 \(a\)。
定义节点 \(x\) 的父亲为 \(fa(x)\),根 \(rt\) 满足 \(fa(rt)=rt\)。
定义节点 \(x\) 的深度 \(dep(x)\) 为其到根简单路径上所有边权和。
有 \(m\) 次操作:
1 l r:对于 \(l \le i \le r\), \(a_i := fa(a_i)\) 。
2 l r:查询对于 \(l \le i \le r\),最小的 \(dep(a_i)\)。\(1 \le n,m \le 2 \times 10^5\)。
感觉就很复杂的题目。
考虑 分块。
对于每一个整块而言,如果块内有 \(x\) 在 \(y\) 上面,那么 \(y\) 是没用的。
这样的 \(y\) 是不需要统计的,
所以如果我们暴力维护每一个点所在位置,每一次往上跳的时候,
如果一个点跳到了块内有一个点跳过的位置,那么这个点就没有用了。
于是对于每一个块,它只会把树上的每一个点遍历一次,
均摊下来的复杂度是 \(\mathcal O(n \sqrt n)\) 的。
再来考虑剩下来的散块。
发现我们希望快速往上面跳 \(k\) 次祖先。
于是我们可以采用重链剖分去重构即可。
由于这题卡空间,所以需要用到逐块处理的技巧,对于每一个块分别处理。
注意树剖跳 \(k\) 级祖先的写法!!!小心常数。代码。
Code
inline int find(int u,int k){
if(dep[u]-1<=k) return rt;
while(dfn[u]-dfn[top[u]]+1<=k) k-=dfn[u]-dfn[top[u]]+1,u=fa[top[u]];
return rev[dfn[u]-k];//不需要暴力跳!
}
int c[N],st[N];
bool vis[N],inv[N];
inline void sol(int id){
int L=(id-1)*B+1,R=min(id*B,n),tag=0,tmp=0,tp=0;
res=inf;
for(int i=1;i<=n;i++)
vis[i]=inv[i]=c[i]=st[i]=0;
for(int i=L;i<=R;i++)
if(!vis[a[i]]) vis[a[i]]=inv[i]=1,st[++tp]=i,res=min(res,d[a[i]]);
for(int i=1;i<=m;i++){
int l=max(q[i].l,L),r=min(q[i].r,R);
if(l>r) continue;
if(q[i].op==1){
if(l==L&&r==R){
tmp=tp;
tp=0,++tag;
for(int i=1;i<=tmp;i++){
c[st[i]]++;
a[st[i]]=fa[a[st[i]]];
if(vis[a[st[i]]]) inv[st[i]]=0;
else{
st[++tp]=st[i];
res=min(res,d[a[st[i]]]);
vis[a[st[i]]]=1;
}
}
}else{
for(int j=l;j<=r;j++){
a[j]=find(a[j],tag-c[j]+1);
c[j]=tag;
if(!vis[a[j]]){
res=min(res,d[a[j]]);
vis[a[j]]=1;
if(!inv[j]) st[++tp]=j,inv[j]=1;
}
}
}
}else{
if(l==L&&r==R) ans[i]=min(ans[i],res);
else
for(int j=l;j<=r;j++)
ans[i]=min(ans[i],d[a[j]=find(a[j],tag-c[j])]),c[j]=tag;
}
}
}
int main(){
/*2024.3.25 H_W_Y P6779 [Ynoi2009] rla1rmdq 分块 + 均摊*/
ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
cin>>n>>m>>rt;
for(int i=1,u,v,w;i<n;i++) cin>>u>>v>>w,add(u,v,w);
dfs1(rt,rt);dfs2(rt,rt);
for(int i=1;i<=n;i++) cin>>a[i],bl[i]=(i-1)/B+1;
for(int i=1;i<=m;i++) cin>>q[i].op>>q[i].l>>q[i].r,ans[i]=inf;
for(int i=1;i<=bl[n];i++) sol(i);
for(int i=1;i<=m;i++) if(q[i].op==2) cout<<ans[i]<<'\n';
return 0;
}
P7446 Ynoi2007 - 分块逐块处理
给定一棵大小为 \(n\) 的 \(1\) 为根节点的树,树用如下方式给出:输入 \(a_2,a_3,\dots,a_n\),保证 \(1\leq a_i<i\),将 \(a_i\) 与 \(i\) 连边形成一棵树。
接下来有 \(m\) 次操作,操作有两种:
1 l r x令 \(a_i=\max(a_i-x,1)(l\leq i\leq r)\)。2 u v查询在当前的 \(a\) 数组构成的树上 \(u,v\) 的 LCA。\(2\leq n,q\leq 4\times 10^5\),\(2\leq l\leq r\leq n\),\(1\leq x\leq 4\times 10^5\),\(1\leq u,v\leq n\)。
被 smb 秒了。/bx,上一道题相当于它的铺垫吧。
我们同样考虑分块,每个点维护它下一次跳到的位置 \(fa_i\) 和第一次跳出块的地方 \(pa_i\)。
考虑每一次修改,对于散块我们暴力重构,但是整块呢?
由于每次的 \(x \ge 1\),所以对于每一个块,最多做这样的整块修改 \(\sqrt n\) 次后所有的元素的 \(pa_i=fa_i\) 了。
所以当修改次数 \(\le \sqrt n\) 时,我们就直接暴力重构整个块;
而之后就直接对于整块打标记即可。
跳的时候类似于倍增往上跳就可以了。
总时间复杂度 \(\mathcal O(n \sqrt n)\)。代码。
P5063 Ynoi2014 - 分块
线段树是一种特殊的二叉树,满足以下性质:
每个点和一个区间对应,且有一个整数权值;
根节点对应的区间是 \([1,n]\);
如果一个点对应的区间是 \([l,r]\),且 \(l<r\),那么它的左孩子和右孩子分别对应区间 \([l,m]\) 和 \([m+1,r]\),其中 \(m=\lfloor\frac{l+r}{2}\rfloor\);
如果一个点对应的区间是 \([l,r]\),且 \(l=r\),那么这个点是叶子;
如果一个点不是叶子,那么它的权值等于左孩子和右孩子的权值之和。
珂朵莉需要维护一棵线段树,叶子的权值初始为 \(0\),接下来会进行 \(m\) 次操作:
操作 \(1\):给出 \(l,r,a\),对每个 \(x\)(\(l\leq x\leq r\)),将 \([x,x]\) 对应的叶子的权值加上 \(a\),非叶节点的权值相应变化;
操作 \(2\):给出 \(l,r,a\),询问有多少个线段树上的点,满足这个点对应的区间被 \([l,r]\) 包含,且权值小于等于 \(a\)。
\(1 \le n,m \le 10^5\)。
崩。
对于一棵线段树,最多只有 \(O(\log n)\) 个长度不同的节点。
而不同长度的区间,修改是非常不好维护的,所以我们对于每一种节点大小分层,维护一个数据结构:
- 区间加
- 单点修改
- 区间 rank
这是经典问题,归约可以证明上界是 \(O(m \sqrt n)\)。
可以证明线段树的每层只有 \(O(1)\) 种不同大小的节点,那么我们的总时间复杂度是 \(O( m \sqrt n + m \sqrt {\frac n 2} + m \sqrt {\frac n 4} +\cdots ) = O(m \sqrt n)\)。
实现需要比较精细,否则要卡常的。代码。
Code
#include <bits/stdc++.h>
using namespace std;
#define ll long long
const int N=1e5+5;
int mp[N],tp=0,n,m;
struct Nod{
int n,len,T,S;
struct Nd{
int l,r;
ll v;
Nd(int L=0,int R=0,ll V=0){l=L,r=R,v=V;}
bool operator <(const Nd &a) const{return v<a.v;}
}A[N];
struct Bl{
int L,R,lm,rm;
ll tag;
Bl(int a=0,int b=0,int c=0,int d=0,ll t=0){L=a,R=b,lm=c,rm=d,tag=t;}
bool operator <(const Bl &a) const{return rm<a.rm;}
}B[405];
void init(){
S=sqrt(n),T=0;
while(B[T].R<n){
++T;
B[T].L=B[T-1].R+1;
B[T].R=B[T-1].R+S;
}
B[T].R=n;
for(int i=1;i<=T;i++) B[i].lm=A[B[i].L].l,B[i].rm=A[B[i].R].r;
}
void upd(int x,int l,int r,ll v){
for(int i=B[x].L;i<=B[x].R;i++){
if(A[i].l>r||A[i].r<l) continue;
A[i].v+=1ll*(min(r,A[i].r)-max(l,A[i].l)+1)*v;
}
sort(A+B[x].L,A+B[x].R+1);
}
void Upd(int l,int r,ll v){
int x=lower_bound(B+1,B+T+1,Bl(-1,-1,-1,l,-1))-B;
if(x>T) return;
if(B[x].lm<=l&&B[x].rm>=r){
if(B[x].lm==l&&B[x].rm==r) B[x].tag+=1ll*len*v;
else upd(x,l,r,v);
return;
}
if(B[x].lm<l) upd(x,l,r,v),++x;
while(x<=T&&B[x].rm<=r) B[x++].tag+=1ll*len*v;
if(x>T) return;
if(B[x].lm<=r) upd(x,l,r,v);
}
ll qry(int x,bool fl,int l,int r,ll v){
if(fl) return upper_bound(A+B[x].L,A+B[x].R+1,Nd(-1,-1,v-B[x].tag))-A-B[x].L;
ll res=0;
for(int i=B[x].L;i<=B[x].R;i++)
res+=(A[i].l>=l&&A[i].r<=r&&A[i].v<=v-B[x].tag);
return res;
}
ll Qry(int l,int r,ll v){
int x=lower_bound(B+1,B+T+1,Bl(-1,-1,-1,l,-1))-B;
if(x>T) return 0;
if(B[x].lm<=l&&B[x].rm>=r){
if(B[x].lm==l&&B[x].rm==r) return qry(x,1,l,r,v);
return qry(x,0,l,r,v);
}
ll res=0;
if(B[x].lm<l) res+=qry(x,0,l,r,v),++x;
while(x<=T&&B[x].rm<=r) res+=qry(x,1,l,r,v),++x;
if(x>T) return res;
if(B[x].lm<=r) res+=qry(x,0,l,r,v);
return res;
}
}G[40];
#define mid ((l+r)>>1)
void build(int l,int r){
int len=r-l+1;
if(!mp[len]) mp[len]=++tp,G[tp].len=len;
++G[mp[len]].n;
int nw=G[mp[len]].n;
G[mp[len]].A[nw].l=l;
G[mp[len]].A[nw].r=r;
if(l==r) return;
build(l,mid),build(mid+1,r);
}
void Upd(int l,int r,ll v){
for(int i=1;i<=tp;i++) G[i].Upd(l,r,v);
}
ll Qry(int l,int r,ll v){
ll res=0;
for(int i=1;i<=tp;i++) res+=G[i].Qry(l,r,v);
return res;
}
int main(){
/*2024.3.28 H_W_Y P5063 [Ynoi2014] 置身天上之森 分块*/
ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
cin>>n>>m;
build(1,n);
for(int i=1;i<=tp;i++) G[i].init();
while(m--){
int op,l,r,a;
cin>>op>>l>>r>>a;
if(op==1) Upd(l,r,a);
else cout<<Qry(l,r,a)<<'\n';
}
return 0;
}
P3810 【模板】三维偏序 - 树套树
有 $ n $ 个元素,第 $ i $ 个元素有 $ a_i,b_i,c_i $ 三个属性,设 $ f(i) $ 表示满足 $ a_j \leq a_i $ 且 $ b_j \leq b_i $ 且 $ c_j \leq c_i $ 且 $ j \ne i $ 的 \(j\) 的数量。
对于 $ d \in [0, n) $,求 $ f(i) = d $ 的数量。
$ 1 \leq n \leq 10^5$,$1 \leq a_i, b_i, c_i \le k \leq 2 \times 10^5 $。
板板(我没写过),用 cdq 和 sts 都可以完成。
接下来的题目主要是思路,因为后面实现时所用到的 cdq 和 sts 是本质相同(思路不会有变化)。
这里放一个 cdq 的板子,可能是树套树都打得挺熟的。
Code
#include <bits/stdc++.h>
using namespace std;
const int N=2e5+5;
int n,m,ans[N],sz[N],cnt=0,t[N],tr[N];
struct node{
int x,y,z,id;
bool operator <(const node &rhs) const{
if(x!=rhs.x) return x<rhs.x;
if(y!=rhs.y) return y<rhs.y;
return z<rhs.z;
}
bool operator ==(const node &rhs) const{return (x==rhs.x&&y==rhs.y&&z==rhs.z);}
bool operator !=(const node &rhs) const{return (x!=rhs.x||y!=rhs.y||z!=rhs.z);}
}a[N],b[N];
int lowbit(int x){return x&(-x);}
void add(int x,int val){for(int i=x;i<=m;i+=lowbit(i)) tr[i]+=val;}
int qry(int x){int res=0;for(int i=x;i>0;i-=lowbit(i)) res+=tr[i];return res;}
void cdq(int l,int r){
if(l==r) return ;
int mid=((l+r)>>1);
cdq(l,mid);cdq(mid+1,r);
int i=l,j=mid+1,nw=l;
while(i<=mid&&j<=r){
if(a[i].y<=a[j].y){
add(a[i].z,sz[a[i].id]);
b[nw]=a[i];++nw;++i;
}else{
t[a[j].id]+=qry(a[j].z);
b[nw]=a[j];++nw;++j;
}
}
while(j<=r){
t[a[j].id]+=qry(a[j].z);
b[nw]=a[j];++nw;++j;
}
for(int p=l;p<i;p++) add(a[p].z,-sz[a[p].id]);
while(i<=mid) b[nw]=a[i],++nw,++i;
for(int p=l;p<=r;p++) a[p]=b[p];
}
int main(){
/*2023.12.7 H_W_Y P3810 【模板】三维偏序(陌上花开) cdq*/
ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
cin>>n>>m;
for(int i=1;i<=n;i++) cin>>a[i].x>>a[i].y>>a[i].z;
sort(a+1,a+n+1);
for(int i=1;i<=n;i++){if(a[i]!=a[i-1]) b[++cnt]=a[i];++sz[cnt];}
for(int i=1;i<=cnt;i++) a[i]=b[i],a[i].id=i;
cdq(1,cnt);
for(int i=1;i<=cnt;i++) ans[t[i]+sz[i]-1]+=sz[i];
for(int i=0;i<n;i++) cout<<ans[i]<<'\n';
return 0;
}
P4054 计数问题 - 树套树
一个 \(n\times m\) 的方格,初始时每个格子有一个整数权值。接下来每次有 \(2\) 种操作:
- 改变一个格子的权值;
- 求一个子矩阵中某种特定权值出现的个数。
\(1 \le n,m \le 300,1 \le Q \le 2 \times 10^5,1 \le c \le 100\)。
很明显是一个带修改的三维偏序(可以树套树套树完成)。
发现权值是很小的,
所以我们直接用 \(100\) 个数据结构去维护,于是就变成二维数点问题了。
Code
#include <bits/stdc++.h>
using namespace std;
const int N=305;
int n,m,a[N][N],tr[N][N][105],q;
int lowbit(int i){return i&(-i);}
void add(int x,int y,int col,int val){
for(int i=x;i<=n;i+=lowbit(i))
for(int j=y;j<=m;j+=lowbit(j))
tr[i][j][col]+=val;
}
int qry(int x,int y,int col){
int res=0;
for(int i=x;i>=1;i-=lowbit(i))
for(int j=y;j>=1;j-=lowbit(j))
res+=tr[i][j][col];
return res;
}
int main(){
/*2023.12.7 H_W_Y P4054 [JSOI2009] 计数问题 BIT*/
ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
cin>>n>>m;
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
cin>>a[i][j],add(i,j,a[i][j],1);
cin>>q;
for(int i=1,op,x,y,l,r,c;i<=q;i++){
cin>>op;
if(op==1){
cin>>x>>y>>c;
add(x,y,a[x][y],-1);
add(x,y,c,1);a[x][y]=c;
}
else{
cin>>x>>l>>y>>r>>c;
cout<<(qry(l,r,c)-qry(x-1,r,c)-qry(l,y-1,c)+qry(x-1,y-1,c))<<'\n';
}
}
return 0;
}
P3157+P3759 动态逆序对 - 树套树 + cdq 分治
即带修改,维护 全局 逆序对数。
有 \(n\) 个点,每个点两个属性 \(a_i,b_i\)。
每次修改一个点的 \(b_i\),维护有多少点对 \((i,j)\) 满足 \([a_i \lt a_j \& \& b_ i \gt b_j]\)
容易发现把 \(a\) 数组作为横坐标,\(b\) 数组作为纵坐标,
于是我们就把问题转化成了一个二维数点问题。
一个点的贡献是它右下角的点数,
在修改的时候我们只需要统计好它左上角和右下角的点数,
减去它对答案的贡献即可,这都是好理解的。
于是我们只需要维护一个树套树完成即可。
Code
#include <bits/stdc++.h>
using namespace std;
#define ll long long
const int N=1e5+5;
int n,m,a[N],idx=0,rt[N],pos[N];
ll ans=0;
struct sgt{int cnt,s[2];}tr[N*300];
#define mid ((l+r)>>1)
#define lc(p) tr[p].s[0]
#define rc(p) tr[p].s[1]
void pu(int p){tr[p].cnt=tr[lc(p)].cnt+tr[rc(p)].cnt;}
void upd(int l,int r,int &p,int x,int val){
if(!p) p=++idx;
if(l==r) return tr[p].cnt+=val,void();
if(x<=mid) upd(l,mid,lc(p),x,val);
else upd(mid+1,r,rc(p),x,val);pu(p);
}
int qry(int l,int r,int p,int x,int y){
if(!p) return 0;
if(x<=l&&y>=r) return tr[p].cnt;
if(y<=mid) return qry(l,mid,lc(p),x,y);
if(x>mid) return qry(mid+1,r,rc(p),x,y);
return qry(l,mid,lc(p),x,y)+qry(mid+1,r,rc(p),x,y);
}
int lowbit(int i){return i&(-i);}
void add(int x,int y,int val){for(int i=x;i<=n;i+=lowbit(i)) upd(1,n,rt[i],y,val);}
int ask(int x,int l,int r){
int res=0;
for(int i=x;i>=1;i-=lowbit(i)) res+=qry(1,n,rt[i],l,r);
return res;
}
int main(){
/*2023.12.7 H_W_Y P3157 [CQOI2011] 动态逆序对 STS*/
ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
cin>>n>>m;
for(int i=1;i<=n;i++) cin>>a[i],pos[a[i]]=i,ans+=1ll*ask(i-1,a[i],n),add(i,a[i],1);
for(int i=1,x;i<=m;i++){
cin>>x;
cout<<ans<<'\n';
ans-=1ll*(ask(n,1,x-1)-ask(pos[x]-1,1,x-1)+ask(pos[x]-1,x+1,n));
add(pos[x],x,-1);
}
return 0;
}
直接忘记取模(还不是取没取完的问题)
Code
#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define pll pair<ll,int>
#define fi first
#define se second
const ll mod=1e9+7;
pll operator +(const pll &x,const pll &y){return {(x.fi+y.fi)%mod,x.se+y.se};}
const int N=1e5+5;
int n,m,a[N],v[N],pos[N],rev[N];
ll ans=0;
namespace SGT{
struct node{int s[2],cnt;ll val;}tr[N*200];
int idx=0;
#define mid ((l+r)>>1)
#define lc(p) tr[p].s[0]
#define rc(p) tr[p].s[1]
void pu(int p){
tr[p].val=(tr[lc(p)].val+tr[rc(p)].val)%mod;
tr[p].cnt=tr[lc(p)].cnt+tr[rc(p)].cnt;
}
void upd(int l,int r,int &p,int x,int val){
if(!p) p=++idx;
if(l==r){
tr[p].val+=1ll*val;
tr[p].cnt=(tr[p].val>0);
return;
}
if(x<=mid) upd(l,mid,lc(p),x,val);
else upd(mid+1,r,rc(p),x,val);pu(p);
}
pll qry(int l,int r,int &p,int x,int y){
if(!p) return {0,0};
if(x<=l&&y>=r) return {tr[p].val,tr[p].cnt};
if(y<=mid) return qry(l,mid,lc(p),x,y);
if(x>mid) return qry(mid+1,r,rc(p),x,y);
return qry(l,mid,lc(p),x,y)+qry(mid+1,r,rc(p),x,y);
}
}
namespace BIT{
int rt[N];
int lowbit(int i){return i&(-i);}
void upd(int x,int y,int val){for(int i=x;i<=n;i+=lowbit(i)) SGT::upd(1,n,rt[i],y,val);}
pll qry(int x,int l,int r){
pll res={0,0};
for(int i=x;i>=1;i-=lowbit(i)) res=res+SGT::qry(1,n,rt[i],l,r);
return res;
}
}
using namespace BIT;
ll find(int x,int l,int r,int val){pll nw=qry(x,l,r);return (1ll*nw.se*val%mod+nw.fi%mod)%mod;}
ll ask(int p,int val,int V){return (find(n,1,val-1,V)-find(p-1,1,val-1,V)+find(p-1,val+1,n,V)+mod)%mod;}
int main(){
/*2023.12.7 H_W_Y P3759 [TJOI2017] 不勤劳的图书管理员 STS*/
ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
cin>>n>>m;
for(int i=1;i<=n;i++){
cin>>a[i]>>v[i],upd(i,a[i],v[i]);
pll nw=qry(i-1,a[i]+1,n);
(ans+=1ll*v[i]*nw.se%mod+nw.fi)%=mod;
pos[i]=rev[i]=i;
}
for(int i=1,x,y;i<=m;i++){
cin>>x>>y;x=rev[x],y=rev[y];
(ans+=mod-ask(pos[x],a[x],v[x]))%=mod;upd(pos[x],a[x],-v[x]);
(ans+=mod-ask(pos[y],a[y],v[y]))%=mod;upd(pos[y],a[y],-v[y]);
swap(pos[x],pos[y]);rev[pos[x]]=x,rev[pos[y]]=y;
upd(pos[x],a[x],v[x]);(ans+=ask(pos[x],a[x],v[x]))%=mod;
upd(pos[y],a[y],v[y]);(ans+=ask(pos[y],a[y],v[y]))%=mod;
cout<<ans<<'\n';
}
return 0;
}
再放上一个 cdq 的写法。(感觉挺有用的)
Code
#include <bits/stdc++.h>
using namespace std;
#define ll long long
const int N=2e5+5;
int n,m,a[N],pos[N],cnt=0,tr[N];
ll ans[N];
struct node{
int op,v,pos,id;
bool operator <(const node &rhs) const{return pos<rhs.pos;}
}c[N];
int lowbit(int i){return i&(-i);}
void add(int x,int val){for(int i=x;i<=n;i+=lowbit(i)) tr[i]+=val;}
int qry(int x){int res=0;for(int i=x;i>0;i-=lowbit(i)) res+=tr[i];return res;}
#define mid ((l+r)>>1)
void cdq(int l,int r){
if(l==r) return ;
cdq(l,mid);cdq(mid+1,r);
sort(c+l,c+mid+1);sort(c+mid+1,c+r+1);
int j=l;
for(int i=mid+1;i<=r;i++){
while(j<=mid&&c[j].pos<=c[i].pos) add(c[j].v,c[j].op),++j;
ans[c[i].id]+=1ll*c[i].op*(qry(n)-qry(c[i].v));
}
for(int i=l;i<j;i++) add(c[i].v,-c[i].op);
j=mid;
for(int i=r;i>mid;i--){
while(j>=l&&c[j].pos>=c[i].pos) add(c[j].v,c[j].op),--j;
ans[c[i].id]+=1ll*c[i].op*qry(c[i].v-1);
}
for(int i=mid;i>j;i--) add(c[i].v,-c[i].op);
}
int main(){
/*2023.12.8 H_W_Y P3157 [CQOI2011] 动态逆序对 cdq*/
ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
cin>>n>>m;
for(int i=1;i<=n;i++) cin>>a[i],pos[a[i]]=i,c[++cnt]=(node){1,a[i],i,0};
for(int i=1,x;i<=m;i++) cin>>x,c[++cnt]=(node){-1,x,pos[x],i};
cdq(1,cnt);
for(int i=1;i<=m;i++) ans[i]+=ans[i-1];
for(int i=0;i<m;i++) cout<<ans[i]<<'\n';
return 0;
}
P3332 K大数查询 - 树套树
你需要维护 \(n\) 个可重整数集,集合的编号从 \(1\) 到 \(n\)。
这些集合初始都是空集,有 \(m\) 个操作:
1 l r c:表示将 \(c\) 加入到编号在 \([l,r]\) 内的集合中2 l r c:表示查询编号在 \([l,r]\) 内的集合的并集中,第 \(c\) 大的数是多少。注意可重集的并是不去除重复元素的,如 \(\{1,1,4\}\cup\{5,1,4\}=\{1,1,4,5,1,4\}\)。
\(1 \le n,m \le 5 \times 10^4\)。
感觉就是很明显的树套树。
第一反应是用线段树套权值线段树,但是这样还需要线段树合并,直接寄。
我们为什么不能反过来想一下呢?
发现可以直接权值线段树套区间线段树,这样二分就方便了许多。
于是这道题就做完了。
Code
#include <bits/stdc++.h>
using namespace std;
#define ll long long
const int N=1e5+5;
int n,m,mx;
struct sgt{int s[2];ll t,v;}tr[N*100];
#define mid ((l+r)>>1)
namespace SGT1{
struct sgt{int s[2];ll t,v;}tr[N*100];
int idx=0;
#define lc tr[p].s[0]
#define rc tr[p].s[1]
void pu(int p){tr[p].v=tr[lc].v+tr[rc].v;};
void pd(int l,int r,int p){
if(!tr[p].t) return ;
if(!lc) lc=++idx;
if(!rc) rc=++idx;
tr[lc].t+=tr[p].t,tr[lc].v+=1ll*(mid-l+1)*tr[p].t;
tr[rc].t+=tr[p].t,tr[rc].v+=1ll*(r-mid)*tr[p].t;
tr[p].t=0;
}
void upd(int l,int r,int &p,int x,int y,int val){
if(!p) p=++idx;
if(x<=l&&y>=r){
tr[p].t+=val;
tr[p].v+=1ll*val*(r-l+1);
return;
}pd(l,r,p);
if(x<=mid) upd(l,mid,lc,x,y,val);
if(y>mid) upd(mid+1,r,rc,x,y,val);pu(p);
}
ll qry(int l,int r,int &p,int x,int y){
if(!p) return 0;
if(x<=l&&y>=r) return tr[p].v;
pd(l,r,p);
if(y<=mid) return qry(l,mid,lc,x,y);
if(x>mid) return qry(mid+1,r,rc,x,y);
return qry(l,mid,lc,x,y)+qry(mid+1,r,rc,x,y);
}
#undef lc
#undef rc
}
namespace SGT2{
int rt[N<<2];
#define lson l,mid,p<<1
#define rson mid+1,r,p<<1|1
void upd(int l,int r,int p,int c,int x,int y){
SGT1::upd(1,n,rt[p],x,y,1);
if(l==r) return;
(c<=mid)?upd(lson,c,x,y):upd(rson,c,x,y);
}
int qry(int l,int r,int p,ll c,int x,int y){
if(l==r) return l;
ll rs=SGT1::qry(1,n,rt[p<<1|1],x,y);
if(c<=rs) return qry(rson,c,x,y);
return qry(lson,c-rs,x,y);
}
}
using namespace SGT2;
int main(){
/*2023.12.7 H_W_Y P3332 [ZJOI2013] K大数查询 STS*/
ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
cin>>n>>m;mx=n*2;
for(int i=1,op,l,r;i<=m;i++){
cin>>op>>l>>r;
if(op==1){
int c;cin>>c;
upd(1,mx,1,c+n,l,r);
}else{
ll c;cin>>c;
int nw=qry(1,mx,1,c,l,r)-n;
cout<<((nw>0)?nw:(nw-1))<<'\n';
}
}
return 0;
}
P9068 本质不同逆序对 - cdq 分治
P9068 [Ynoi Easy Round 2022] 超人机械 TEST_95
给定一个序列 \(a\) ,我们定义一个二元组 \((i,j)\) 为一个逆序对当且仅当 \(i<j\) 且 \(a_i>a_j\) 。定义两个逆序对 \((i_1,j_1),(i_2,j_2)\) 本质不同 当且仅当 \(a_{i_1}\ne a_{i_2}\) 或 \(a_{j_1}\ne a_{j_2}\) 。
现在给出 \(a\) 序列,问本质不同逆序对个数。
这还不够。
现在有 \(q\) 组修改,每一次修改形如 \(x~y\) 表示修改 \(a_x\) 为 \(y\) ,每一次修改 不互相独立 ,即这一次修改会影响到后面的所有修改。
你需要对于每一次修改输出序列本质不同逆序对个数。
为了体现本题的不同解法,本题不同测试点拥有不同的时空限制。
\(1 \le n,q \le 10^5\)。
考虑直接树套树做法,
发现本质不同其实就是把每一种颜色的第一次出现位置和最后一次出现位置提出来,
分别用两个数据结构维护。
对于每一个颜色,我们在第一次出现位置中找这个颜色与前面组成的逆序对数,
在最后一次出现位置中找这个颜色与后面组成的逆序对数。
于是用两个树套树维护即可。
但是发现一个严重的问题,空间限制是 50MB 的,
于是只能离线下来用 cdq 分治解决了。
但是直接维护两个数组是不好做的,
所以我们考虑把它分成两种,用一个区间维护即可。
Code
#include <bits/stdc++.h>
using namespace std;
#define ll long long
const int N=1e5+5,M=1e6+5;
int n,m,a[N],cntl,cntr,tr[N],col[N],nw;
ll ans[N];
set<int> s[N];
struct node{int x,l,r,id;}ql[M],qr[M];
bool cmp1 (const node &x,const node &y){return x.x<y.x;}
bool cmp2 (const node &x,const node &y){return x.x>y.x;}
void add(int x,int y,int id){
bool mn=false,mx=false;
if(s[y].empty()) mn=mx=true;
if(!s[y].empty()&&x<*s[y].begin())
ql[++cntl]=(node){y,*s[y].begin(),-1,0},mn=true;
if(!s[y].empty()&&x>*s[y].rbegin())
qr[++cntr]=(node){y,*s[y].rbegin(),-1,0},mx=true;
if(mn){
ql[++cntl]=(node){y,x,1,0};
int nxt=(s[y].empty()?n+1:*s[y].begin());
if(x+1<=nxt-1) qr[++cntr]=(node){y,x+1,nxt-1,id};
}
if(mx){
qr[++cntr]=(node){y,x,1,0};
int pre=(s[y].empty()?0:*s[y].rbegin());
if(pre+1<=x-1) ql[++cntl]=(node){y,pre+1,x-1,id};
}
s[y].insert(x);
}
void del(int x,int y,int id){
bool mn=false,mx=false;
s[y].erase(x);
if(s[y].empty()) mn=mx=true;
if(!s[y].empty()&&x<*s[y].begin())
ql[++cntl]=(node){y,*s[y].begin(),1,0},mn=true;
if(!s[y].empty()&&x>*s[y].rbegin())
qr[++cntr]=(node){y,*s[y].rbegin(),1,0},mx=true;
if(mn){
ql[++cntl]=(node){y,x,-1,0};
int nxt=(s[y].empty()?n+1:*s[y].begin());
if(x+1<=nxt-1) qr[++cntr]=(node){y,x+1,nxt-1,-id};
}
if(mx){
qr[++cntr]=(node){y,x,-1,0};
int pre=(s[y].empty()?0:*s[y].rbegin());
if(pre+1<=x-1) ql[++cntl]=(node){y,pre+1,x-1,-id};
}
}
#define mid ((l+r)>>1)
int c(int p){return (col[p]==nw?tr[p]:0);}
int lowbit(int i){return i&(-i);}
void upd(int x,int val){for(int i=x;i<=n;i+=lowbit(i)) tr[i]=c(i)+val,col[i]=nw;}
int qry(int x){int res=0;for(int i=x;i>=1;i-=lowbit(i)) res+=c(i);return res;}
template<typename Cmp>
void cdq(int l,int r,node *q,Cmp cmp){
if(l==r) return;
cdq(l,mid,q,cmp);cdq(mid+1,r,q,cmp);
++nw;
for(int i=mid+1,j=l;i<=r;i++){
while(j<=mid&&cmp(q[j],q[i])){
if(!q[j].id) upd(q[j].l,q[j].r);
++j;
}
if(!q[i].id) continue;
int res=qry(q[i].r)-qry(q[i].l-1);
if(q[i].id>0) ans[q[i].id]+=res;
else ans[-q[i].id]-=res;
}
inplace_merge(q+l,q+mid+1,q+r+1,cmp);
}
int main(){
/*2023.12.9 H_W_Y P9068 [Ynoi Easy Round 2022] 超人机械 TEST_95 cdq*/
ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
cin>>n;
for(int i=1;i<=n;i++) cin>>a[i],add(i,a[i],1);
cin>>m;++m;
for(int i=2,x,y;i<=m;i++) cin>>x>>y,del(x,a[x],i),add(x,a[x]=y,i);
cdq(1,cntl,ql,cmp2);cdq(1,cntr,qr,cmp1);
for(int i=1;i<=m;i++) cout<<(ans[i]+=ans[i-1])<<'\n';
return 0;
}
其实 cdq 也没有想象那么难。
P4690 Ynoi2016 镜中的昆虫 - 树套树
维护一个长为 \(n\) 的序列 \(a[i]\),有 \(m\) 次操作。
- 将区间 \([l,r]\) 的值修改为 \(x\)。
- 询问区间 \([l,r]\) 出现了多少种不同的数。
也就是说同一个数出现多次只算一个。
\(1 \le n,m \le 10^5\)。
首先第一个操作看起来就很像颜色段均摊。
我们用相同的思路,去维护每个点和它上一次出现的位置。
发现对于一个颜色段,中间的 \(pre\) 其实就是指向 \(i-1\) 的,
无论如何改颜色都是不会改变,
所以每一次修改就变成了单点修改。
于是直接用一个树套树维护一下即可。
P3242 接水果 - 树套树标记永久化
树,先给了一些路径,每个路径有个权值。
然后每次查询给一个路径,求包含这个路径的最开始给的路径中,权值 \(kth\) 是多少?
\(1 \le n,p,q \le 4 \times 10^4\)。
很有意思的一道题啊。
首先发现最开始给出的路径,
它能覆盖的路径是有一个区间的。
而对于后面的询问,一条路径包含它当且仅当两个端点都在这条路的两个端点的子树中。
于是一个权值能覆盖的区间就容易在二维平面上面用矩阵表示出来。
Conclusion
- 与因子有关的问题都可以考虑将质数分成几类去完成。(P5071 [Ynoi2015] 此时此刻的光辉)
- 树套树时可以考虑枚举哪两个树,有关一段区间集合并问题可以考虑 权值线段树套区间线段树。(P3332 K大数查询)


 浙公网安备 33010602011771号
浙公网安备 33010602011771号