球&盒

球盒求和问题是组合数学中比较经典的模型，许多刚入门的小白（比如我）就经常会被球与盒子之间你认不出我，我认得出你这样混乱的关系残忍杀害。
为了方便之后的学习数数的时候忘了可以过来贺一下，这里对这些球盒计数做一个总结。

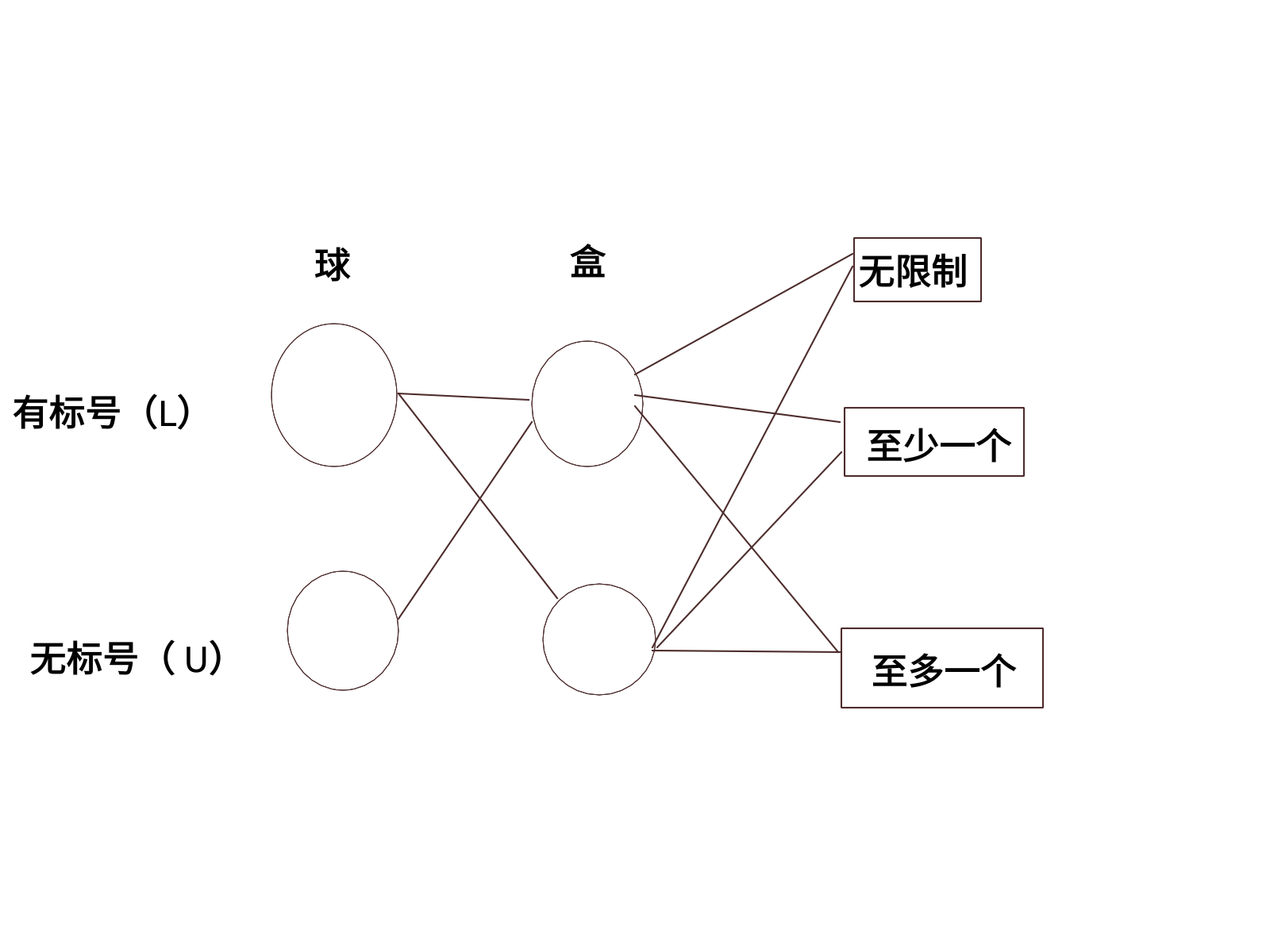
首先，根据乘法原理可以得到一共有 \(2\times 2 \times 3=12\) 种情况，接下来将对这十二种情况一一分析。

以下都设有 \(n\) 个球， \(m\) 个盒子。

---

1.LLA（球不同盒不同无限制）

对于每一个球，它都有 \(m\) 种放置方案。
根据乘法原理，可以得到总方案数为 \(m^n\) 。
时间复杂度 \(O(\log n)\)

---

2.LLB（球不同盒不同至少放一个球）

设 \(f_{i}\) 表示有 \(n\) 个球的时候 \(i\) 个盒子不为空的方案数。
那么 LLA 的情况还可以换一种表示方式，即：
\( \begin{aligned} n^m&=\sum^{m}_{i=0} \begin{pmatrix} m\\ i\\ \end{pmatrix} f_{i} \end{aligned} \)
它的意义是去枚举这 \(m\) 个盒子中有多少个是非空的，从 \(m\) 个的盒子中选出 \(i\) 个非空的方案数再乘上 \(n\) 个球放入这 \(i\) 个盒子的方案数。
这个东西是标准的二项式反演式子。 应该可以用更简单的方法得到
于是可以得到：
\( \begin{aligned} f_{m}&=\sum^{m}_{i=0} (-1)^{m-i} \begin{pmatrix} m\\ m-i\\ \end{pmatrix} i^n \end{aligned} \)

于是可以在 \(O(n)\) 的时间复杂度内得到 \(f_{m}\) 。
对它做一个变形，可以得到：

\[\begin{aligned} f_{m}&=\sum^{m}_{i=0} (-1)^{m-i} \begin{pmatrix} m\\ m-i\\ \end{pmatrix} i^n \\ &=m!\sum^{m}_{i=0}\frac{(-1)^{m-i}}{(m-i)!}\frac{i^n}{i!} \end{aligned} \]

注意到这是一个卷积的形式，所以可以在 \(O(n \log n)\) 的时间复杂度内得到一行（n确定的时候）的结果。

---

3.LLC（球不同盒不同至多放一个球）

首先 \(m<n\) 的时候方案数为 0。
当 \(m\geq n\) 的时候，首先要从 \(m\) 个盒子中选择 \(n\) 个出来用来装球，同时又因为选出来的这 \(n\) 个盒子都是不同的，所以这 \(n\) 个盒子的每一种排列都对应着一种不同的方案数。
所以可以得到方案数为\( \begin{pmatrix} m\\ n\\ \end{pmatrix} n! \)

---

4.LUB（球不同盒同至少放一个）

这里选择先讲LUB而不是LUA是因为得到LUA的方法是建立在得到LUB上的。
可以发现LUB的情况恰好就是LLB除了一个 \(m!\) ，因为此时的盒子是没有标号的，因此之前的每一种有标号的情况都相当于是无标号的情况的 \(m\) 个盒子的所有排列情况。
式子长这样：

\[\begin{aligned} f_{m}&=\frac{1}{m!}\sum^{m}_{i=0} (-1)^{m-i} \begin{pmatrix} m\\ m-i\\ \end{pmatrix} i^n \\ &=\sum^{m}_{i=0}\frac{(-1)^{m-i}}{(m-i)!}\frac{i^n}{i!} \end{aligned} \]

因此同LLB的情况，可以在 \(O(n)\) 的时间复杂度内得到单点的值，在 \(O(n \log n)\) 的时间复杂度内得到一行的结果。

同时，把盒子看成是一个集合，这还是第二类斯特林数的定义。
上面的式子也是 \( \begin{Bmatrix} n\\ m\\ \end{Bmatrix} \)的通项公式。

---

5.LUA（球不同盒同无限制）

可以将其分类，分成有 \(0\) 个空盒子， \(1\) 个空盒子...... \(m\) 个空盒子的情况。
设 \(f_{i}\) 为LUB中的方案数，可以得到LUA的方案数\( \sum^{m}_{i=0} f_{i} \)。

---

6.LUC（球不同盒同至多放一个）

盒相同，然后最后所有的球肯定都是在盒子里面的，所以本质上就只有一种方案。
因此可以得到公式：\( \left \{ \begin{aligned} 0,m<n\\ 1,m\geq n\\ \end{aligned} \right. \)

---

7.ULB（球同盒不同至少放一个）

隔板法的经典模型。
等价于往 \(n-1\) 个空隙中插入 \(m-1\) 个隔板，每个隔板所隔出来的区间代表盒子。
可以得到方案数为\( \begin{pmatrix} n-1\\ m-1\\ \end{pmatrix} \)

---

8.ULA（球同盒不同无限制）

跟前面几个 \(B\) 转 \(A\) 的套路一样，枚举有多少个盒子是空的，因为这里的盒子是有标号的，所以记得还要算上选空盒子的方案数。
通项公式：

\[\begin{aligned} f_{m}&=\sum^{m}_{i=1} \begin{pmatrix} m\\ i\\ \end{pmatrix} \begin{pmatrix} n-1\\ i-1\\ \end{pmatrix}\\ \end{aligned} \]

这个依旧可以转换成卷积的形式，有兴趣的话可以自己推导一下，这里就不赘述了。
仍然是单点 \(O(n)\) ，一行 \(O(n \log n)\)。

---

9.ULC（球同盒不同至多放一个）

这个等价于从 \(m\) 个物品中选出 \(n\) 个来的方案数。
公式\( \begin{pmatrix} m\\ n\\ \end{pmatrix} \)

---

10.UUA（球同盒同无限制）

这个感觉上非常难统计。
为了不算重，可以默认将盒子按照装的球的个数从大到小排序，每次枚举当前已经用了 \(i\) 个盒子，已经用了 \(j\)个球。

我们定义两种操作：
1.给当前加上一个空盒子。
2.给当前所有的盒子全部放一个球。
不难发现这样可以保证盒子按照了球的个数从大到小排序，还能够操作出所有的方案，并且每一种操作方案和每一种放置方案是一一对应的。

举个例子

当前要得到序列 {4,4,3,1,0}

一.执行两次操作1。

二.执行一次操作2。

三.执行一次操作1。

四.执行两次操作2。

五.执行一次操作1。

六.执行一次操作2。

七.执行一次操作1。

因此，可以得到这样的一个dp式子：

\( \begin{aligned} f_{i,j}&=f_{i-1,j}+f_{i,j-i} \end{aligned} \)
将其写成生成函数的形式：
\( \begin{aligned} F_{m}&=F_{n-1}+x^{i} F_{m} \\ F_{m}(1-x^n)&=F_{m-1}\\ F_{m}&=\frac{F_{m-1}}{(1-x^m)}\\ &=\frac{F_{m-2}}{(1-x^m)(1-x^{m-1})}\\ &\ \ \vdots\\ &=\frac{1}{\prod^{m}_{i=1}(1-x^i)}\\ \end{aligned} \)
如果做过 付公主的背包，那么到这里问题已经解决了。
这里简单推导一下（如果接下来的内容有不会的可以看我的这一篇笔记）。

\( \begin{aligned} F_{m}&=\frac{1}{\prod^{m}_{i=1}(1-x^i)}\\ \ln F_{m}&=\ln(\frac{1}{\prod^{m}_{i=1}(1-x^i)})\\ &=\sum^{m}_{i=1}\ln\frac{1}{1-x^i}\\ &=\sum^{m}_{i=1}\sum^{\infty}_{j=1}\frac{x^{ij}}{j}\\ \end{aligned} \)
其中的 \(\ln F_{m}\) 可以暴力枚举来构造，由于后面是个调和级数，复杂度是 \(O(n \log n)\)。
$F_{m}= \exp(\ln F_{m}) $，所以可以在 \(O(n \log n)\) 的时间复杂度内得到 \(F_{m}\)，即UUA的一列（\(m\)确定的时候）
答案是\(F_{m}[x^n]\)

---

11.UUB（球同盒同至少放一个）

可以在一开始先钦定给每一个盒子放一个球，就成了UUA的情况，答案是\(F_{m}[x^{n-m}]\)（如果 \(n<m\) 则为0）。

---

12.UUC（球同盒同至多放一个）

这个应该很明显，和LUC是一样的，方案数为\( \left \{ \begin{aligned} 0,m<n\\ 1,m\geq n\\ \end{aligned} \right. \)

---

至此，球与盒之间的关系似乎也没有那么混乱了。
然而，根据条件的不同，可能某天又冒出别的情况，什么UUZ啊，BBAasdlkjfwepufjflkjxcv啊。
重要的是上面的推导思想，如果其中一种情况不好解决，那不妨先试着加上/去掉一些条件，看看是不是会好统计一些，在通过容斥之类的转换来得到正确的方案。