XJ训练2021.4.15

真谛，都在skのass里面啊...

---

T1：期望
首先对于题目不难得到这样的一个式子：
\( \begin{aligned} ans&=\sum^{n}_{i=1}E(siz_i(n-siz_i)))\\ &=\sum^{n}_{i=1}nE(siz_i)-E(siz_i^2)\\ \end{aligned} \)
可以发现难点在于后面的 \(E(siz_i^2)\)。
转换成组合意义，\(E(siz_i^2)\) 等价于在以 \(i\) 为根的子树内选两个点的方案数。
那么考虑点对 \((u,v)\) ，它们造成的贡献的点必然是两点之间的 \(lca(u,v)\) 以及它的祖先。
那么\( \begin{aligned} E(siz_i^2)&=\sum_{i=1}^{n}\sum_{u}^{}\sum_{v}^{}[i是lca(u,v)的祖先] \end{aligned} \)。
这样子不好统计，考虑到把所有的贡献都存储到 \(lca(u,v)\) 上。
\( \begin{aligned} 原式&=dep_{i}\sum^{n}_{i=1}[i=lca(u,v)] \end{aligned} \)
这样子看起来似乎阳间一些了还是很阴间。
前面的 \(dep_{i}\) 跟后面的式子可以分开来算，难点在有后面的sigma,这里设它为 \(f\)。
假设现在有一颗以 \(i\) 为根的树，现在往内加入一个 \(u\) 点，它会产生多少贡献？

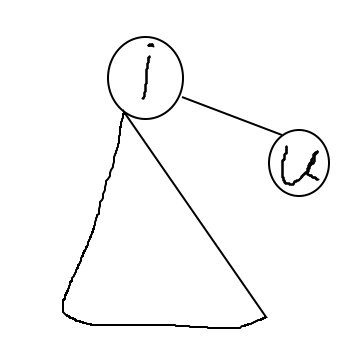
这样看下来似乎是 \(f_{i}+=siz_{i}\times siz_{u}\)

但是有一些别的情况：

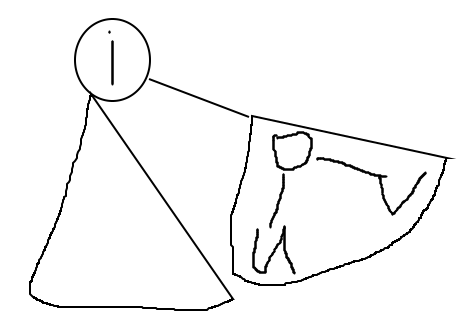
这种情况不应该被统计，却被额外计算了。额外计算的部分是什么？恰好是 \(f_{lca(u,v)}\)。
于是，可以做一个简单容斥，有 \(f_{u}=siz_u^2-\sum^{}_{i\in u}ass_{i}^2f_{i}\) ，其中 \(ass_{i}\) 表示 \(i\) 出现在以 \(u\) 为根的树中的概率skのass。
此处的 \(ass_{i}\) 需要平方的原因是因为此处的 \(f_{i}\) 实质上是一个平方的期望，因此 \(ass_{i}\) 也需要平方（或者也可以理解为u在去掉贡献的时候和v在去掉贡献的时候都要乘上\(ass_{i}\)）。 需要两个skのass
\(ass_{i}\) 比较好求，直接枚举 \(i\) 在 \(u\) 内的父亲 \(j\) ，不难得到 \(ass_{i}=\frac{\sum^{}_{}ass_{j}}{\sigma(j)}\)，其中 \(\sigma(j)\)表示 \(j\) 的因数个数。 想必到这里你已经弄透了skのass
由于 \(u|i,u|j\) ，所以在代码中可以直接让 \(i,j\) 除一个 \(u\) ，方便枚举。
同时，还可以发现有了 \(ass\) 数组之后，计算一棵树的期望 \(siz\) 也能顺便解决了skのass的恩惠。
最后做一个统计，注意一些细节就可以了。
最后，一起赞美skのass罢

访问skの尻

#include<bits/stdc++.h>
using namespace std;
#define il inline
#define ri register int
#define ll long long
#define ui unsigned int
il ll read(){
    bool f=true;ll x=0;
    register char ch=getchar();
    while(ch<'0'||ch>'9') {if(ch=='-') f=false;ch=getchar();}
    while(ch>='0'&&ch<='9') x=(x<<3)+(x<<1)+(ch^48),ch=getchar();
    if(f) return x;
    return ~(--x);
}
il void write(const ll &x){if(x>9) write(x/10);putchar(x%10+'0');}
il void print(const ll &x) {x<0?putchar('-'),write(~(x-1)):write(x);putchar('\n');}
il ll max(const ll &a,const ll &b){return a>b?a:b;}
il ll min(const ll &a,const ll &b){return a<b?a:b;}
ll n,mod;
il ll ksm(ll d,ll t){
    ll res=1;
    for(;t;t>>=1,d=d*d%mod)
        if(t&1) res=res*d%mod;
    return res;
}
const int MAXN=3e5+7;
ll f[MAXN],dep[MAXN],inv[MAXN];
/*  
尻のパワー
ass no Powa
*/
vector<int> vec[MAXN];//因子
il ll add(ll x,ll y){return (x+=y)<mod?x:x-mod;}
ll ass[MAXN],ans;
int main(){
    n=read(),mod=read();
    for(ri i=1;i<=n;++i) inv[i]=ksm(i,mod-2);
    for(ri i=1;i<=n;++i){
        for(ri j=2;i*j<=n;++j){
            vec[i*j].push_back(i);
        }
    }
    dep[1]=0;
    for(ri i=2;i<=n;++i){
        ll w=inv[vec[i].size()];
        for(ri j=0;j<vec[i].size();++j){
            int v=vec[i][j];
            dep[i]=add(dep[i],dep[v]+1);
        }
        dep[i]=dep[i]*w%mod;
    }//计算深度期望
    for(ri i=n;i>=2;--i){
        ass[1]=1;
        ll tot=1,num=n/i;//此处的j实际上对应的点是i*j
        for(ri j=2;j<=num;++j){
            ll res=0;
            for(ri k=0;k<vec[j].size();++k){//诶举可能的父亲
                int v=vec[j][k];
                res=add(res,ass[v]);
            }
            ass[j]=res*inv[vec[i*j].size()]%mod;
            tot=add(tot,1*ass[j]);
        }
        f[i]=tot*tot%mod;
        for(ri j=2;j<=num;++j) 
            f[i]=add(f[i],mod-ass[j]*ass[j]%mod*f[i*j]%mod);
    }
    for(ri i=1;i<=n;++i){
        ans=add(ans,((dep[i]*n-dep[i]*f[i])%mod+mod)%mod);
    }
    print(add(ans,ans));//题目中每条路径要算两次
    return 0;
}

那么接下来，探讨的是skの尻。
为和会出现这么奇妙的情况？
skの尻恰好是这题最美妙、最简介却有最有力的证明。
如果没有了skの尻，我想必还在为究竟该如何理解这些东西的含义而苦恼。
skの尻，真理之门！

说人话就是因为设了个叫skの尻的数组结果最后把上面这一段式子的含义解释通了，而且还恰好能联系上前面别的信息，非常神奇。这一切，都是skの尻的指引！
一起信仰skの尻罢。

---

T2:贪心
这题XJ上贴的题解讲的很清楚了，所以这里就不讲了。

Code

#include<bits/stdc++.h>
using namespace std;
#define il inline
#define ri register int
#define ll long long
#define ui unsigned int
il ll read(){
    bool f=true;ll x=0;
    register char ch=getchar();
    while(ch<'0'||ch>'9') {if(ch=='-') f=false;ch=getchar();}
    while(ch>='0'&&ch<='9') x=(x<<3)+(x<<1)+(ch^48),ch=getchar();
    if(f) return x;
    return ~(--x);
}
il void write(const ll &x){if(x>9) write(x/10);putchar(x%10+'0');}
il void print(const ll &x) {x<0?putchar('-'),write(~(x-1)):write(x);putchar('\n');}
il ll max(const ll &a,const ll &b){return a>b?a:b;}
il ll min(const ll &a,const ll &b){return a<b?a:b;}
vector<int> T;
struct line
{
    int l,r;
    bool operator<(const line &p)const{
        return r>p.r;
    }
};
bool cmp(line x,line y){
    return x.l<y.l;
}
ll n;
const int MAXN=5e5+7;
int h[MAXN],d[MAXN],sta[MAXN],top,cnt,siz;
priority_queue<line> q;
vector<line> vec;
int main(){
    n=read();
    for(ri i=1;i<=n;++i) h[i]=read(),d[i]=read();
    for(ri i=2;i<=n;++i){
        if(h[i]!=h[i-1]) ++cnt;
        if(d[i]!=d[i-1]) ++cnt;
        if(h[i]!=h[i-1]&&d[i]!=d[i-1]) T.push_back(i),++siz;
    }
    sta[++top]=2;
    for(ri i=2;i<=n;++i){
        if(d[i]==d[i-1]){
            sta[top]=i+1;
            continue;
        }
        while(top&&d[i]<d[sta[top]-1])  --top;
        if(top&&d[i]==d[sta[top]-1]){
            vec.push_back((line){sta[top],i});
            ++siz;
            top--;
        }
        sta[++top]=i+1;
    }
    top=0;
    sta[++top]=2;
    for(ri i=2;i<=n;++i){
        if(h[i]==h[i-1]){
            sta[top]=i+1;
            continue;
        }
        while(top&&h[i]<h[sta[top]-1])  --top;
        if(top&&h[i]==h[sta[top]-1]){
             vec.push_back((line){sta[top],i});
            ++siz;
            top--;
        }
        sta[++top]=i+1;
    }
    top=0;
    sort(vec.begin(),vec.end(),cmp);
    for(ri i=0,j=0;i<T.size();++i){
        while(j<vec.size()&&vec[j].l<=T[i]) q.push(vec[j++]);
        while(!q.empty()&&q.top().r<T[i]) q.pop();
        if(!q.empty()){
            q.pop();
            --siz;
        }
    }
    print(cnt-siz);
    return 0;
}