AGC026 解题记录
春归结局也挺好的...
A:DP
乱搞做法一大堆,反正是 \(A\) 题,数据范围也小,直接枚举上一维的颜色做dp。
B:简单数论
首先先特判一些情况。
1.b>d
这种情况会出现入不敷出,显然无法无限购买。
2.a<b
第一天就买不了
3.c>b
再去掉上面两种情况之后c>b的时候一定可以无限买,很显然,不解释了。
先令 \(a = a\mod b\) ,显然不影响答案。
去掉上面几种情况后,开始推式子。
设已经买了 \(x\) 次,进货了 \(y\) 次,那么可以得到
注意到式 \(2\) 和式 \(3\) 形式一样,最后肯定有一边变成 \(0\) ,另一边变成 \(\gcd(x,y)\)。
因此,等价于是否存在整数 \(k\) 满足 \(k\times \gcd(x,y)\in(L,R)\)。
时间复杂度\(O(T \log V)\)。
Code
#include<bits/stdc++.h>
using namespace std;
#define il inline
#define ri register int
#define ll long long
#define ui unsigned int
il ll read(){
bool f=true;ll x=0;
register char ch=getchar();
while(ch<'0'||ch>'9') {if(ch=='-') f=false;ch=getchar();}
while(ch>='0'&&ch<='9') x=(x<<3)+(x<<1)+(ch^48),ch=getchar();
if(f) return x;
return ~(--x);
}
il void write(const ll &x){if(x>9) write(x/10);putchar(x%10+'0');}
il void print(const ll &x) {x<0?putchar('-'),write(~(x-1)):write(x);putchar('\n');}
il ll max(const ll &a,const ll &b){return a>b?a:b;}
il ll min(const ll &a,const ll &b){return a<b?a:b;}
ll a,b,c,d;
il ll gcd(ll x,ll y){
for(;y;x%=y,swap(x,y));
return x;
}
int main(){
for(ri t=read();t;--t){
a=read(),b=read(),c=read(),d=read();
if(a<b){
puts("No");
continue;
}
if(b>d){
puts("No");
continue;
}
if(c>b){
puts("Yes");
continue;
}
a%=b;
if(a>c){
puts("No");
continue;
}
ll l=c-a,r=b-a;
ll g=gcd(b,d),x=(l+g-1)/g*g;
while(x<=l) x+=g;
if(x<r) puts("No");
else puts("Yes");
}
return 0;
}
C:折半搜索+哈希
这题挺简单的,就是有点难
这题都快把折半搜索写在题面里了,考虑如何折半。
如果前半部分搜出来的两种颜色字符串哈希值是 \((x_l,y_l)\) ,后半部分搜出来是 \((x_r,y_r)\),那么这两个能匹配起来的条件是:
\(
\begin{aligned}
x_l+D^n x_r&=y_r+D^n y_l\\
x_l+D^n y_l&=y_r -D^n x_r\\
\end{aligned}
\)
到这一步就不用多解释了,直接上map。
时间复杂度 \(O(n2^n)\)。
Code
#include<bits/stdc++.h>
using namespace std;
#define il inline
#define ri register int
#define ll long long
#define ui unsigned int
il ll read(){
bool f=true;ll x=0;
register char ch=getchar();
while(ch<'0'||ch>'9') {if(ch=='-') f=false;ch=getchar();}
while(ch>='0'&&ch<='9') x=(x<<3)+(x<<1)+(ch^48),ch=getchar();
if(f) return x;
return ~(--x);
}
il void write(const ll &x){if(x>9) write(x/10);putchar(x%10+'0');}
il void print(const ll &x) {x<0?putchar('-'),write(~(x-1)):write(x);putchar('\n');}
il ll max(const ll &a,const ll &b){return a>b?a:b;}
il ll min(const ll &a,const ll &b){return a<b?a:b;}
char s[40];
int n;
const ll mod1=998244353,mod2=1e9+7,d=131;
struct node
{
ll x,y;
bool operator==(const node &p)const{
return x==p.x&&y==p.y;
}
ll operator %(const ll &p)const{
return x*y%p;
}
node operator *(const node &p)const{
return (node){x*p.x%mod1,y*p.y%mod2};
}
node operator +(const node &p)const{
return (node){(x+p.x)%mod1,(y+p.y)%mod2};
}
node operator -(const node &p)const{
return (node){(x-p.x+mod1)%mod1,(y-p.y+mod2)%mod2};
}
}B,D;
struct hmap{
static const int P=2e6+3,M=3e7+10;
int hed[M],nxt[M],cnt;node val[M];ll as[M];
bool count(node x){
int c=hed[x%P];
while(c){
if(val[c]==x) return 1;
c=nxt[c];
}return 0;
}
ll& operator [](node x){
int c=hed[x%P];
while(c){
if(val[c]==x) return as[c];
c=nxt[c];
}
++cnt;val[cnt]=x;nxt[cnt]=hed[x%P];hed[x%P]=cnt;
return as[cnt];
}
int size(){return cnt;}
}f;
#define T pair<node,node>
ll base[42],ans;
T solve(ll x){
node l=(node){0,0},r=(node){0,0};
for(ri i=0;i<n;++i){
if(base[i]&x){
l=l*D;
l=l+(node){s[i],s[i]};
}
}
for(ri i=n-1;~i;--i){
if(!(base[i]&x)){
r=r*D;
r=r+(node){s[i],s[i]};
}
}
return (T){l,r};
}
int main(){
n=read();
scanf("%s",s);
D=B=(node){d,d};
base[0]=1;
for(ri i=1;i<=n;++i) B=B*D,base[i]=base[i-1]<<1;
for(ri i=0;i<base[n];++i){
T now=solve(i);
f[now.first*B-now.second]++;
}
for(ri i=0;i<n;++i)s[i]=s[n+i];
for(ri i=0;i<base[n];++i){
T now=solve(i);
if(f.count(now.second*B-now.first))ans+=f[now.second*B-now.first];
}
print(ans);
return 0;
}
D:笛卡尔树+DP
挺不错一道题,对着题解想了很久都没想出来。
首先不难发现,如果是一个 \(n\times m\) 的矩阵,可以先枚举第一行,然后往上转移。
分两类:
1.上一行是 \(010101...\) 形式的,即 \(01\) 交错。
这种时候有两种可能,要么是和上一行完全一样,要么是上一行取反。
而且这两种情况依旧是 \(01\) 交错。
2.除了 1 中所有情况。
只能是上一行取反,所以这一行依旧是情况 2。
所以可以得到这样的DP方程:\( \left\{ \begin{aligned} &f_{i,0}=f_{i-1,0}\\ &f_{i,1}=2f_{i-1,1}\\ \end{aligned} \right. \)
其中初始化是 \(f_{1,1}=2,f_{1,0}=2^m-f_{1,1}\) 。
接下来考虑在柱状图中要如何转移。
可以发现,当柱状图是一个上凸的时候,可以从上往下进行转移,下面给出一个例子(本人在这个地方想了很久)。
\(
\begin{matrix}
&&?\\
&?&?&?\\
?&?&?&?&?
\end{matrix}
\)
假设最后需要知道的是\(f_{3}\)(从上往下标号)。
首先有\(f_{1,0}=0,f_{1,1}=2\)。
考虑第二行:
\(
\begin{matrix}
&?\\
?&?&?\\
\end{matrix}
\)
现在先求\(f_{2,1}\)。
先不管中间,把两边填起来,用两种方法,分别是\(
\begin{matrix}
0&?&0\\
\end{matrix}
\)和\(\begin{matrix}
1&?&1\\
\end{matrix}
\)。
不难发现中间在两种方案中中间可以填的方案数都等价于\(f_{1,1}\)。
因为中间需要填上的是一段交错的 \(01\) ,并且填的方案已经确定了,剩下的都可以和上一行的 \(f_{1,1}\) 一一对应。
\(f_{2,0}\) 则可以先统计所有的方案,再减去 \(f_{2,1}\) 。
这一部分的转移
void solve(int u){
f[u][0]=ksm(2,len[u]),f[u][1]=2;
for(ri i=0;i<g[u].size();++i){
int v=g[u][i];
solve(v);
f[u][0]=mul(f[u][0],f[v][0]+2*f[v][1]);
f[u][1]=mul(f[u][1],f[v][1]);
}
f[u][0]=add(f[u][0],mod-f[u][1]);
f[u][1]=mul(f[u][1],ksm(2,h[u]-1));
}
而当有多个上凸的时候,从上往下考虑,它们先是不联通,直到某一行把它们连到了一起。
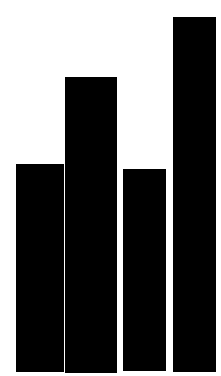
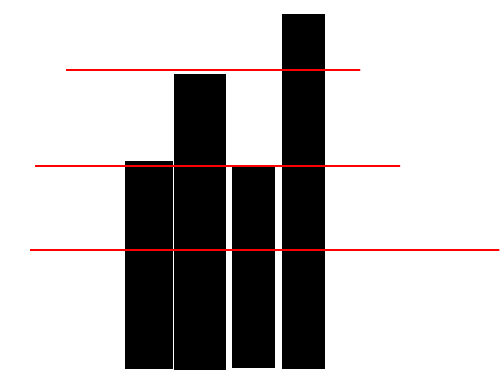
这不是一棵树吗?而且是一颗笛卡尔树!
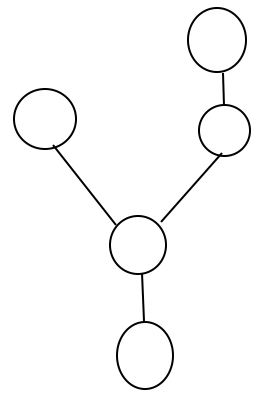
于是,就可以建树跑树型DP了。
理论上建树可以 \(O(n)\) ,由于快速幂部分都是 \(2\) ,可以提前预处理实现光速幂做到预处理 \(O(\sqrt{V})\) ,查询 \(O(1)\)。
所以总复杂度是 $ O(n+\sqrt{V}) $ ,完全可以把 \(n\) 设为 \(10^7\) 。结果只有100
Code
#include<bits/stdc++.h>
using namespace std;
#define il inline
#define ri register int
#define ll long long
#define ui unsigned int
il ll read(){
bool f=true;ll x=0;
register char ch=getchar();
while(ch<'0'||ch>'9') {if(ch=='-') f=false;ch=getchar();}
while(ch>='0'&&ch<='9') x=(x<<3)+(x<<1)+(ch^48),ch=getchar();
if(f) return x;
return ~(--x);
}
il void write(const ll &x){if(x>9) write(x/10);putchar(x%10+'0');}
il void print(const ll &x) {x<0?putchar('-'),write(~(x-1)):write(x);putchar('\n');}
il ll max(const ll &a,const ll &b){return a>b?a:b;}
il ll min(const ll &a,const ll &b){return a<b?a:b;}
const int MAXN=129;
/*
考虑从上往下一层一层构造
可以建一颗笛卡尔树跑树型DP
不过这棵笛卡尔树有点不太一样?
*/
ll f[MAXN][2],a[MAXN];//0表示没有间隔,1表示有间隔
#define lc u<<1
#define rc u<<1|1
#define pii pair<int,int>
struct Seg
{
struct T
{
int l,r;
pii v;
}t[MAXN<<2];
void build(int u,int l,int r){
t[u].l=l,t[u].r=r;
if(l==r){
t[u].v=(pii){a[l],l};
return;
}
int mid=(l+r)>>1;
build(lc,l,mid);
build(rc,mid+1,r);
t[u].v=min(t[lc].v,t[rc].v);
}
pii query(int u,int l,int r){
if(t[u].l==l&&t[u].r==r) return t[u].v;
int mid=(t[u].l+t[u].r)>>1;
if(r<=mid) return query(lc,l,r);
else if(l>mid) return query(rc,l,r);
else return min(query(lc,l,mid),query(rc,mid+1,r));
}
}T;
ll n,root;
ll L[MAXN],R[MAXN],h[MAXN],len[MAXN];
int cnt;
vector<int> g[MAXN];
int build(int l,int r){//有用单调栈实现O(n)建树的方法,不过这里不是复杂度瓶颈,线段树比较好写
vector<int> vec;
vec.clear();
int u=++cnt;
len[u]=r-l+1,L[u]=l,R[u]=r,h[u]=T.query(1,l,r).first;
vec.push_back(l-1);
for(ri now=l;now<=r;){//把深度相同的丢到一起
pii res=T.query(1,now,r);
if(res.first>h[u]) break;
vec.push_back(res.second);
now=res.second+1;
}
vec.push_back(r+1);
for(ri i=0;i<vec.size()-1;++i){
if(vec[i]+1>vec[i+1]-1) continue;
int v=build(vec[i]+1,vec[i+1]-1);
g[u].push_back(v);
h[v]-=h[u];
len[u]-=R[v]-L[v]+1;
}
return u;
}
const ll mod =1e9+7;
il ll ksm(ll d,ll t){
ll res=1;
for(;t;t>>=1,d=d*d%mod)
if(t&1) res=res*d%mod;
return res;
}
il ll add(ll x,ll y){return (x+=y)<mod?x:x-mod;}
il ll mul(ll x,ll y){return x*y%mod;}
void solve(int u){
f[u][0]=ksm(2,len[u]),f[u][1]=2;
for(ri i=0;i<g[u].size();++i){
int v=g[u][i];
solve(v);
f[u][0]=mul(f[u][0],f[v][0]+2*f[v][1]);
f[u][1]=mul(f[u][1],f[v][1]);
}
f[u][0]=add(f[u][0],mod-f[u][1]);
f[u][1]=mul(f[u][1],ksm(2,h[u]-1));
}
int main(){
n=read();
for(ri i=1;i<=n;++i) a[i]=read();
T.build(1,1,n);
root=build(1,n);
solve(root);
print(add(f[root][0],f[root][1]));
return 0;
}
E:贪心+模拟
要是想到了点上应该马上就能切。
设 \(a=1,b=-1\) ,那么不难发现从前往后每个极短和为 \(0\) 区间都是互不干扰的。
并且,如果区间开头是 \(a\) ,那么一定有 \(pos_{a_i} < pos_{b_i}\),反之也成立。
这个结论比较显然,手模一下就能发现。
如果能够求出每一段区间的最大字典序,就可以用一个单调栈把它们拼接起来了。
接下来考虑怎么求区间的。
分类讨论:
1.区间开头是 \(a\) 。
那么最优的情况一定是若干段 \(ab\),又有 \(pos_{b_i}<pos_{b_{i+1}}\),所以贪心地能取就取。
2.区间的开头是 \(b\) 。
如果选择了第一个 \(b\) ,设它的下标为 \(l\) ,所对应的 \(a\) 的下标为 \(r\),那么不难发现区间 \((l,r)\) 内的都是 \(b\) ,一定是选择了更优。
这样一直选下去,会发现刚好会一直选到结尾,因为这个区间保证了只有在结尾处的前缀和为 \(0\)。
所以可以枚举从第几个 \(b\) 开始选,记录一下字典序最大的。
上面的操作的总复杂度是 \(O(n^2)\) 的,单调栈过程中的复杂度是 \(O(\sum^{n}_{i=1}L_i)=O(n)\) 所以总复杂度是\(O(n^2)\)。
这一部分的转移
#include<bits/stdc++.h>
using namespace std;
#define il inline
#define ri register int
#define ll long long
#define ui unsigned int
il ll read(){
bool f=true;ll x=0;
register char ch=getchar();
while(ch<'0'||ch>'9') {if(ch=='-') f=false;ch=getchar();}
while(ch>='0'&&ch<='9') x=(x<<3)+(x<<1)+(ch^48),ch=getchar();
if(f) return x;
return ~(--x);
}
il void write(const ll &x){if(x>9) write(x/10);putchar(x%10+'0');}
il void print(const ll &x) {x<0?putchar('-'),write(~(x-1)):write(x);putchar('\n');}
il ll max(const ll &a,const ll &b){return a>b?a:b;}
il ll min(const ll &a,const ll &b){return a<b?a:b;}
const int MAXN=6e3+7;
string b[MAXN];
bool cmp(string &x,string &y){
for(ri i=0,len=min(x.size(),y.size());i<len;++i){
if(x[i]<y[i]) return 1;
if(x[i]>y[i]) return 0;
}
return 0;
}
string check(string &s,int len){
string res;
if(s[0]=='a'){
res="";
for(ri i=0,j=-1;i<len;++i){
if(s[i]=='b') continue;
if(i>j){
res+="ab";
++j;
}
else{
for(ri k=j+1;k<len;++k){
if(s[k]=='b'){
s.erase(s.begin()+k);
len--;
break;
}
}
s.erase(s.begin()+i);
--len;
--i,--j;
}
while(j<len&&s[j]!='b') ++j;
}
return res;
}
res=s;
for(ri i=len/2,j;i;--i){
for(j=0;j<len;++j){
if(s[j]=='b'){
s.erase(s.begin()+j);
--len;
break;
}
}
for(j=0;j<len;++j){
if(s[j]=='a'){
s.erase(s.begin()+j);
--len;
break;
}
}
if(s>res) res=s;
}
return res;
}
char s[MAXN];
int n,top;
int main(){
//freopen("rand.in","r",stdin);
//freopen("1.out","w",stdout);
string res,now;
n=read();
scanf("%s",s+1);
ll sum=0;
for(ri i=1,lst=0;i<=(n<<1);++i){
if(s[i]=='a') sum-=1;
else sum+=1;
if(!sum){
res.clear();
res.resize(i-lst);
for(ri j=lst+1;j<=i;++j) res[j-lst-1]=s[j];
now=check(res,i-lst);
lst=i;
while(top&&cmp(b[top],now)) --top;
b[++top]=now;
}
}
string ans="";
for(ri i=1;i<=top;++i) ans+=b[i];
cout<<ans<<endl;
return 0;
}
F:无中文题面,鸽了。

 伊莉雅😭😭😭😭
伊莉雅😭😭😭😭

 浙公网安备 33010602011771号
浙公网安备 33010602011771号