AT好题记录

AGC020E (2021,3,28)
与其说是难想,倒不如说是想到了却不敢写。
如果没有子集这个限制,询问字符串 \(s_{l,r}\) 的不同合法方案数,暴力怎么做?是不是枚举、枚举、枚举,dp查询
设 \(f(l,r)\) 表示 \(s_{l,r}\) 的不同合法方案数, \(g(l,r)\) 表示 \(s_{l,r}\) 合成为一个开头和结尾分别为 '(',')' 的方案数,那么不难得到非常naive的一个转移式子。
实际上,拓展到了子集上后这个转移式子依旧适用,那么就\(f(s)\) 表示字符串\(s\) 的所有子集的不同合法方案数,\(g(s)\) 表示字符串 \(s\) 的所有子集合成为一个开头和结尾分别为 '(',')' 的方案数。
这个过程加上一个记忆化搜索,跑得飞快,不知道复杂度该怎么证明。
Code
#include<bits/stdc++.h>
using namespace std;
#define il inline
#define ri register int
#define ll long long
#define ui unsigned int
il ll read(){
bool f=true;ll x=0;
register char ch=getchar();
while(ch<'0'||ch>'9') {if(ch=='-') f=false;ch=getchar();}
while(ch>='0'&&ch<='9') x=(x<<3)+(x<<1)+(ch^48),ch=getchar();
if(f) return x;
return ~(--x);
}
il int read(char *s){
int len=0;
register char ch=getchar();
while(ch==' '||ch=='\n') ch=getchar();
while(ch!=' '&&ch!='\n'&&ch!=EOF) s[++len]=ch,ch=getchar();
return len;
}
il void write(const ll &x){if(x>9) write(x/10);putchar(x%10+'0');}
il void print(const ll &x) {x<0?putchar('-'),write(~(x-1)):write(x);putchar('\n');}
il ll max(const ll &a,const ll &b){return a>b?a:b;}
il ll min(const ll &a,const ll &b){return a<b?a:b;}
il ll Plus(ll x,ll y,ll p){return (x+=y)<p?x:x-p;}
il ll operator%(string s,ll p){
ll x=0;
for(ri i=s.length()-1;~i;--i) x=Plus(x<<1,s[i]-'0',p);
return x;
}
struct hmap{
static const int P=2e6+3,M=5e6+10;
int hed[M],nxt[M],cnt;string val[M];ll as[M];
bool count(string x){
int c=hed[x%P];
while(c){
if(val[c]==x) return 1;
c=nxt[c];
}return 0;
}
ll& operator [](string x){
int c=hed[x%P];
while(c){
if(val[c]==x) return as[c];
c=nxt[c];
}
++cnt;val[cnt]=x;nxt[cnt]=hed[x%P];hed[x%P]=cnt;
return as[cnt];
}
int size(){return cnt;}
}f[2];
const ll mod=998244353;
il ll F(int id,string s){
if(f[id].count(s)) return f[id][s];
ll res=0,len=s.length()-1;
if(id){
for(ri i=0;i<=len;++i) res=Plus(res,F(1,s.substr(0,i))*F(0,s.substr(i))%mod,mod);
}
else{
for(ri i=1;i<=len;++i){
if((len+1)%i) continue;
string S(i,'1');
for(ri j=0;j<=len;j+=i){
for(ri k=0;k<i;++k){
if(s[j+k]=='0') S[k]='0';
}
}
res=Plus(res,F(1,S),mod);
}
}
return f[id][s]=res;
}
string s;
int main(){
f[0][""]=f[1][""]=1;
f[0]["1"]=f[1]["1"]=2;
f[0]["0"]=f[1]["0"]=1;
cin>>s;
print(F(1,s));
// cout<<s.substr(1,s.length()-1);
return 0;
}
AGC021D (2021,3,29)
link
这题主要还是一个结论:串 \(T\) 和其反串 \(T'\) 的 最长公共子序列 等于其『最长公共子回文串』。
这个证明其实还是挺显然的,这里给出一个不太严谨的反证法:
设当前的最长公共子序列为 \(S\) ,分别是串 \(s,t\) 里,且\(s\not = t\)
那么此时一定有 \(s=t'\)
那么也肯定有 \(s+t'=s'+t\),即存在梗长的公共子序列 \(s+t'\),与假设矛盾
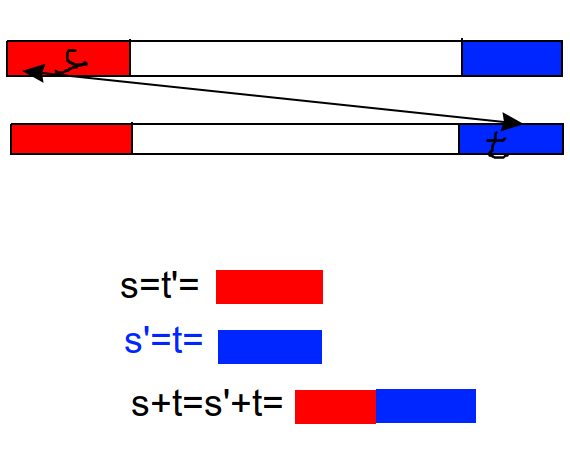
至于求最长公共子回文串部分,直接用一个 \(O(n^2k)\) 的区间dp实现。
Code
#include<bits/stdc++.h>
using namespace std;
#define il inline
#define ri register int
#define ll long long
#define ui unsigned int
il ll read(){
bool f=true;ll x=0;
register char ch=getchar();
while(ch<'0'||ch>'9') {if(ch=='-') f=false;ch=getchar();}
while(ch>='0'&&ch<='9') x=(x<<3)+(x<<1)+(ch^48),ch=getchar();
if(f) return x;
return ~(--x);
}
il int read(char *s){
int len=0;
register char ch=getchar();
while(ch==' '||ch=='\n') ch=getchar();
while(ch!=' '&&ch!='\n'&&ch!=EOF) s[++len]=ch,ch=getchar();
return len;
}
il void write(const ll &x){if(x>9) write(x/10);putchar(x%10+'0');}
il void print(const ll &x) {x<0?putchar('-'),write(~(x-1)):write(x);putchar('\n');}
il ll max(const ll &a,const ll &b){return a>b?a:b;}
il ll min(const ll &a,const ll &b){return a<b?a:b;}
const int MAXN=305;
short f[2][MAXN][MAXN];
char s[MAXN];
int n,t;
int main(){
n=read(s),t=read();// scanf("%s",s+1);
for(ri i=0,o=0;i<=t;++i,o^=1){
memset(f[o],0,sizeof(f[o]));
for(ri j=1;j<=n;++j) f[o][j][j]=1;
for(ri j=1;j<n;++j){
for(ri l=1,r=l+j;r<=n;++l,++r){
f[o][l][r]=max(f[o][l+1][r],f[o][l][r-1]);
if(s[l]==s[r]) f[o][l][r]=max(f[o][l][r],f[o][l+1][r-1]+2);
if(i) f[o][l][r]=max(f[o][l][r],f[o^1][l+1][r-1]+2);
}
}
}
print(f[t&1][1][n]);
return 0;
}
AGC021E (2021,3,29)
link
挺妙的,自己做的时候感觉大概想到点上了,却怎么也推不出最后的式子。
由于题目要求的不同是指最后的操作序列不同,因此只要求有多少种合法序列。
那么对于一个序列,假设它有 \(x\) 个红球, \(y\) 个蓝球:
-
\(x+n\geq y\)
这种情况一定合法,故答案为 \(C^{k}_{x}\)。 -
\(x<y\)
这种情况一定不合法,答案为 \(0\)。 -
\(x=y\)
这种情况不难发现最后一个球一定是 \(B\) ,所以等价于 \(y=x-1\) 的情况,可以归到第 \(4\) 类中去。 -
\(x\in(y,y+n)\)
可以采取这样一种最优策略:钦定一只变色龙专门用来吃蓝球,有红球优先给别的还是蓝色的变色龙,如果有变红的且红球多于蓝球的变色龙,则把这个蓝球给这只变色龙。
这种方法一定是最优策略之一,正确性挺显然的。
同时,也可以发现吃蓝球个数等于红球个数的变色龙至少要有 \(n-(x-y)\) 只,因为要保证剩下的变色龙都能顺利变成红色。
用 R 表示操作序列中有一个红球, B 表示有一个蓝球,那么上面的条件等价于要求最终串中能截取出至少 \(n-(x-y)\) 个 RB,这又等价于对于任意位置的前缀,要满足蓝球比红球多的个数不超过 \(y-(n-(x-y))=x-n\),因为超过了这个值就意味有超过 \(x-n\) 个蓝球无法被匹配,那么最终能够匹配上的个数一定不会达到 \(n-(x-y)\)。
因此,又可以转换为从 \((0,0)\) 走到 \((x,y)\) ,只能向右或者向上,路上不能碰到直线 \(Y-X=x-n+1\)(字母重复了,所以换了大写)。
这是个经典问题,用对称的方法可以得到最后答案为 \(C^{x+y}_{x}-C^{x+y}_{2x-n+1}\)。
结合上面四种情况,其中1,3,4可以用同一个函数完成,2则可以在枚举的时候直接break,无论从哪个方面来讲都很简洁比十多种分讨的不可多得的好题舒服多了。
复杂度\(O(k)\)
Code
#include<bits/stdc++.h>
using namespace std;
#define il inline
#define ri register int
#define ll long long
#define ui unsigned int
il ll read(){
bool f=true;ll x=0;
register char ch=getchar();
while(ch<'0'||ch>'9') {if(ch=='-') f=false;ch=getchar();}
while(ch>='0'&&ch<='9') x=(x<<3)+(x<<1)+(ch^48),ch=getchar();
if(f) return x;
return ~(--x);
}
il int read(char *s){
int len=0;
register char ch=getchar();
while(ch==' '||ch=='\n') ch=getchar();
while(ch!=' '&&ch!='\n'&&ch!=EOF) s[++len]=ch,ch=getchar();
return len;
}
il void write(const ll &x){if(x>9) write(x/10);putchar(x%10+'0');}
il void print(const ll &x) {x<0?putchar('-'),write(~(x-1)):write(x);putchar('\n');}
il ll max(const ll &a,const ll &b){return a>b?a:b;}
il ll min(const ll &a,const ll &b){return a<b?a:b;}
const ll mod =998244353;
il ll ksm(ll d,ll tim){
ll rest=1;
while(tim){
if(tim&1) rest=rest*d%mod;
d=d*d%mod;
tim>>=1;
}
return rest;
}
const int MAXN=5e5+7;
ll jc[MAXN],inv[MAXN];
void init(int n=MAXN-1){
jc[0]=1;
for(ri i=1;i<=n;++i) jc[i]=i*jc[i-1]%mod;
inv[n]=ksm(jc[n],mod-2);
for(ri i=n-1;~i;--i) inv[i]=inv[i+1]*(i+1)%mod;
}
il ll C(ll x,ll y){
if(x<y) return 0;
return jc[x]*inv[y]%mod*inv[x-y]%mod;
}
ll n,k,ans;
ll solve(ll x,ll y){
ll res=0;
res=C(x+y,x);
if(2*x-n+1>=0) res=(res-C(x+y,2*x-n+1)+mod)%mod;
return res;
}
int main(){
init();
n=read(),k=read();
if(n>k){
return !puts("0");
}
for(ri i=k,j=0;i>=j;--i,++j){
if(i==j) ans=(ans+solve(i,j-1))%mod;
else ans=(ans+solve(i,j))%mod;
}
print(ans);
return 0;
}
AGC022E (2021,3,30)
挺神仙的一道题目,之前xza讲过,最后还是没能想起来
草,是x义x讲的,连这个都忘了,我自裁罢
实际上,题目所问的是有多少个合法的序列,于是可以贪心地考虑怎么样的一个序列是合法的。
小贪一波,可以得到这样的结论:
000一定会消掉变成001X的时候剩下的肯定是X,可以直接把0和1抵消- 只要最终保证
1的数量比0多就一定合法(实际上由于整个串的长度是奇数,操作不改变奇偶性,所以只要保证1不比0少就行)
根据上面的性质,可以对其维护一个栈。
如果当前加入的元素是 0 且栈中已经有两个连续的 0 了,就可以把它们变成一个 0。
如果当前加入的元素是 1 且栈顶是 0 ,就把它们抵消,否则入栈。
这样维护不难发现最后栈里 1 比 0 多就一定合法,且 0 的个数不会超过 2,所以当栈中 1 的个数超过了\(2\),可以把它看做是\(2\),两者是等价的。
所以可以设 \(f[i][j][k]\) 表示当前枚举到第 \(i\) 个字符,根据 \(s_i\) 是 0 还是 1 来决定转移,如果是 ? 则两个转移都进行。
一共 \(9\) 种状态,复杂度为 \(O(n)\)
Code
#include<bits/stdc++.h>
using namespace std;
#define il inline
#define ri register int
#define ll long long
#define ui unsigned int
il ll read(){
bool f=true;ll x=0;
register char ch=getchar();
while(ch<'0'||ch>'9') {if(ch=='-') f=false;ch=getchar();}
while(ch>='0'&&ch<='9') x=(x<<3)+(x<<1)+(ch^48),ch=getchar();
if(f) return x;
return ~(--x);
}
il int read(char *s){
int len=0;
register char ch=getchar();
while(ch==' '||ch=='\n') ch=getchar();
while(ch!=' '&&ch!='\n'&&ch!=EOF) s[++len]=ch,ch=getchar();
return len;
}
il void write(const ll &x){if(x>9) write(x/10);putchar(x%10+'0');}
il void print(const ll &x) {x<0?putchar('-'),write(~(x-1)):write(x);putchar('\n');}
il ll max(const ll &a,const ll &b){return a>b?a:b;}
il ll min(const ll &a,const ll &b){return a<b?a:b;}
const int MAXN=3e5+7;
const ll mod =1e9+7;
ll f[2][3][3],n,ans;
char s[MAXN];
int main(){
f[0][0][0]=1;
n=read(s);
for(ri i=1,o=1;i<=n;++i,o^=1){
memset(f[o],0,sizeof(f[o]));
if(s[i]=='0'||s[i]=='?'){
for(ri i=0;i<3;++i){
f[o][i][1]=(f[o][i][1]+f[o^1][i][0]+f[o^1][i][2])%mod;
f[o][i][2]=(f[o][i][2]+f[o^1][i][1])%mod;
}
}
if(s[i]=='1'||s[i]=='?'){
f[o][1][0]=(f[o][1][0]+f[o^1][0][0])%mod;
f[o][2][0]=(f[o][2][0]+f[o^1][1][0]+f[o^1][2][0])%mod;
for(ri i=1;i<3;++i){
f[o][0][i-1]=(f[o][0][i-1]+f[o^1][0][i])%mod;
f[o][1][i-1]=(f[o][1][i-1]+f[o^1][1][i])%mod;
f[o][2][i-1]=(f[o][2][i-1]+f[o^1][2][i])%mod;
}
}
ans=ans;
}
for(ri i=0;i<3;++i){
for(ri j=0;j<=i;++j){
ans=(ans+f[n&1][i][j])%mod;
}
}
print(ans);
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号